どもども。
今回も前回・前々回に引き続き今年の京大入試理系数学の第6問が主題です
問題:http://www.yozemi.ac.jp/nyushi/sokuho/recent/kyoto/zenki/sugaku_ri/mon6.html
前々回:http://blog.goo.ne.jp/mathnegi/e/5db101a423ac4dfec98e19f118e41750
前回:http://blog.goo.ne.jp/mathnegi/e/2943822d5ce9f8720cd2b44d749d8ffd
既に述べたように,この問題は連分数を題材にした確率の問題です。

登場する分数の分子が全て1であるものを正則連分数と呼びます
この連分数を[X_n;X_{n-1},X_{n-2},…,X_1]と書くことにしましょう。
(連分数の表記法としてよく使う方法です)
すなわちY_n=[X_n;X_{n-1},X_{n-2},…,X_1]です
いまは正則連分数[A_1;A_2,A_3,…,A_n,…]としては常に,A_1が整数,A_k(k≧1)は自然数であるもののみを考えるものとします。
またn個の成分で表現できる[A_1;A_2,A_3,…,A_n]型の連分数をn階層の連分数と呼ぶことにしましょう
今回の問題ではX_1,X_2,…,X_nの数字をサイコロの出目で決めよう,という
なかなか面白いことをやっています。
その際に (√3+1)/2≦[X_n;X_{n-1},…,X_1]≦(√3+1) となる確率p_nを
求めなさいというものでしたね~。凄まじいです
前回までは不等式評価と確率漸化式を駆使してこれを解いたので
あまり連分数の色合いはあまり感じられませんでしたので,
今回は(√3+1)と(√3+1)/2の正則連分数表示などを駆使してこの問題に挑んでみたいと思います
さてY_nは有理数ですので,Y_n=(√3+1)/2 または (√3+1) となることは無いです。
すると,条件式: (√3+1)/2≦[X_n;X_{n-1},…,X_1]≦(√3+1) は無理数を含まない形で書き換えられるはずです。
サイコロを振って作られる [X_n;X_{n-1},…,X_1] は 6^n 通りしかないので,
その中にはY_nの最小値と最大値があります。それを用いることで上の条件は書き換えられるってわけです
そんなわけで,(√3+1) と (√3+1)/2 の正則連分数表示を求めるところから始めましょー
x=√3+1 を解とする有理係数2次方程式を利用する方法がこちら

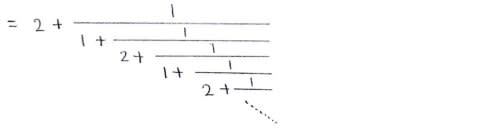
出てきたxをひたすら置き換え続けていくという単純な手法です。
これによって√3+1=[2;1,2,1,2,1,2,1,2,1…]であることが分かりました
もう1つのやり方を紹介します。ガウス記号[ ]を使って実数をひたすら
整数部分と小数部分に分解していくやり方です

√3+1と(√3+1)/2が交互に現われるので(√3+1)/2の連分数表示の方も即座に求められてしまいます
かくて,
√3+1=[2;1,2,1,2,1,2,1,2,1…]
(√3+1)/2=[1;2,1,2,1,2,1,2,1,2…]
であることがわかりました
これを基にして,n階層の正則連分数 a_n,b_n を次のように定めます。

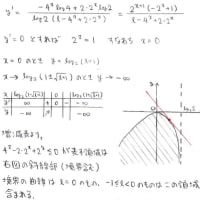
ここで,√3+1とa_nの大小関係に関して次の補題を証明します

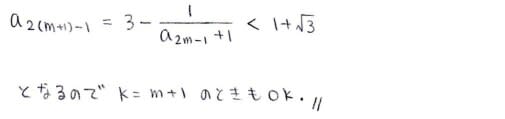
√3+1とa_nの大小関係はnの偶奇によってころころ入れ替わるようです
同様に(√3+1)/2とb_nの大小関係にも触れておきます。

さて,n階層の正則連分数(分数の中に出てくる数字は自然数ばかりのものを考えてます)の中で
最も√3+1に近いのがa_n,(√3+1)/2に最も近いのがb_n になっています。
実数を小数で表示したとき,例えば 3.1415<α<3.1416 を満たすαは
α=3.1415******…… の形で表示されますが,同じようなもので
√3+1<α<a_{2k} を満たすαはやはりα=[2;1,2,1,2,1,…2,1,*,*,*,…](2k階層までは2,1が続く)
という形で表示されます。
そんなわけで, (√3+1)/2≦[X_n;X_{n-1},…,X_1]≦(√3+1) の書き換えが得られます

6^n 個あるY_nの組み合わせのうち,上記の条件を満たすものはいくつあるんでしょうか
実際に場合の数を計算してみます。
どんな要領か知るために,p_2とp_3なんかを求めてみましょう

各階層の分数を大きくしたり小さくしたりというのを使い分けなきゃいけないぽいです

それを踏まえてnの偶奇で状況を分けて考えてみます
更にはX_nが1か2かによっても場合分けします。


(1)~(3)までの3パターンに分類できるので,それぞれの個数を足し合わせればOKです
X_n=2の場合も同様です~

Y_n<a_n なのでa_nは含んではいけません。注意しましょう
あとは足すだけですね
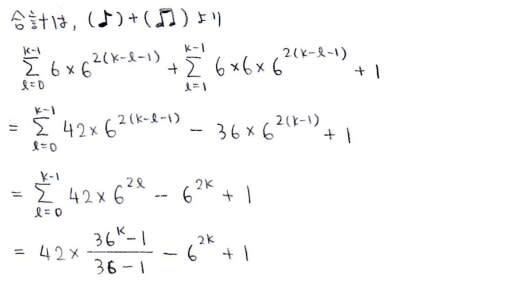

となり,前回までに求めた答えと一致しました

よく見ると1≦ℓ≦k-1みたいな条件式が途中入っていたのでk≧2での議論に
なってたぽいですがk=1でもこの結果は正しいですね。
お次はnが奇数の場合です~~


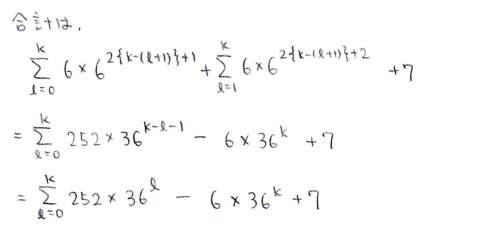
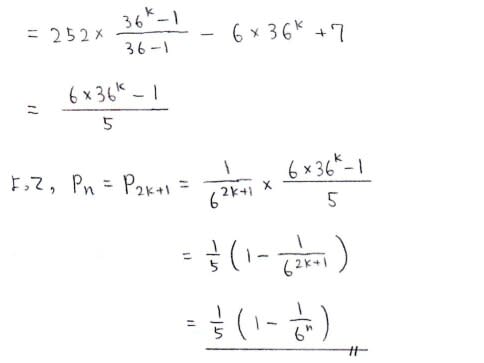
こちらも結果が一致しました
すべてのkに対して合ってます。
…というわけで,長々とした考察になりましたが無事に答えが導けました
しかしながら,そんな苦労しなくても前々回の最初にやったように,
漸化式立ててアッサリスッパリ解いちゃうことが出来ちゃうんですね~
とても面白い問題だったと思います

今回も前回・前々回に引き続き今年の京大入試理系数学の第6問が主題です

問題:http://www.yozemi.ac.jp/nyushi/sokuho/recent/kyoto/zenki/sugaku_ri/mon6.html
前々回:http://blog.goo.ne.jp/mathnegi/e/5db101a423ac4dfec98e19f118e41750
前回:http://blog.goo.ne.jp/mathnegi/e/2943822d5ce9f8720cd2b44d749d8ffd
既に述べたように,この問題は連分数を題材にした確率の問題です。

登場する分数の分子が全て1であるものを正則連分数と呼びます

この連分数を[X_n;X_{n-1},X_{n-2},…,X_1]と書くことにしましょう。
(連分数の表記法としてよく使う方法です)
すなわちY_n=[X_n;X_{n-1},X_{n-2},…,X_1]です

いまは正則連分数[A_1;A_2,A_3,…,A_n,…]としては常に,A_1が整数,A_k(k≧1)は自然数であるもののみを考えるものとします。
またn個の成分で表現できる[A_1;A_2,A_3,…,A_n]型の連分数をn階層の連分数と呼ぶことにしましょう

今回の問題ではX_1,X_2,…,X_nの数字をサイコロの出目で決めよう,という
なかなか面白いことをやっています。
その際に (√3+1)/2≦[X_n;X_{n-1},…,X_1]≦(√3+1) となる確率p_nを
求めなさいというものでしたね~。凄まじいです

前回までは不等式評価と確率漸化式を駆使してこれを解いたので
あまり連分数の色合いはあまり感じられませんでしたので,
今回は(√3+1)と(√3+1)/2の正則連分数表示などを駆使してこの問題に挑んでみたいと思います

さてY_nは有理数ですので,Y_n=(√3+1)/2 または (√3+1) となることは無いです。
すると,条件式: (√3+1)/2≦[X_n;X_{n-1},…,X_1]≦(√3+1) は無理数を含まない形で書き換えられるはずです。
サイコロを振って作られる [X_n;X_{n-1},…,X_1] は 6^n 通りしかないので,
その中にはY_nの最小値と最大値があります。それを用いることで上の条件は書き換えられるってわけです

そんなわけで,(√3+1) と (√3+1)/2 の正則連分数表示を求めるところから始めましょー

x=√3+1 を解とする有理係数2次方程式を利用する方法がこちら


出てきたxをひたすら置き換え続けていくという単純な手法です。
これによって√3+1=[2;1,2,1,2,1,2,1,2,1…]であることが分かりました

もう1つのやり方を紹介します。ガウス記号[ ]を使って実数をひたすら
整数部分と小数部分に分解していくやり方です


√3+1と(√3+1)/2が交互に現われるので(√3+1)/2の連分数表示の方も即座に求められてしまいます

かくて,
√3+1=[2;1,2,1,2,1,2,1,2,1…]
(√3+1)/2=[1;2,1,2,1,2,1,2,1,2…]
であることがわかりました

これを基にして,n階層の正則連分数 a_n,b_n を次のように定めます。

ここで,√3+1とa_nの大小関係に関して次の補題を証明します


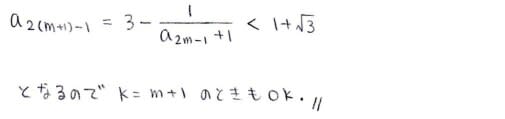
√3+1とa_nの大小関係はnの偶奇によってころころ入れ替わるようです

同様に(√3+1)/2とb_nの大小関係にも触れておきます。

さて,n階層の正則連分数(分数の中に出てくる数字は自然数ばかりのものを考えてます)の中で
最も√3+1に近いのがa_n,(√3+1)/2に最も近いのがb_n になっています。
実数を小数で表示したとき,例えば 3.1415<α<3.1416 を満たすαは
α=3.1415******…… の形で表示されますが,同じようなもので
√3+1<α<a_{2k} を満たすαはやはりα=[2;1,2,1,2,1,…2,1,*,*,*,…](2k階層までは2,1が続く)
という形で表示されます。
そんなわけで, (√3+1)/2≦[X_n;X_{n-1},…,X_1]≦(√3+1) の書き換えが得られます


6^n 個あるY_nの組み合わせのうち,上記の条件を満たすものはいくつあるんでしょうか

実際に場合の数を計算してみます。
どんな要領か知るために,p_2とp_3なんかを求めてみましょう


各階層の分数を大きくしたり小さくしたりというのを使い分けなきゃいけないぽいです


それを踏まえてnの偶奇で状況を分けて考えてみます

更にはX_nが1か2かによっても場合分けします。


(1)~(3)までの3パターンに分類できるので,それぞれの個数を足し合わせればOKです

X_n=2の場合も同様です~

Y_n<a_n なのでa_nは含んではいけません。注意しましょう

あとは足すだけですね

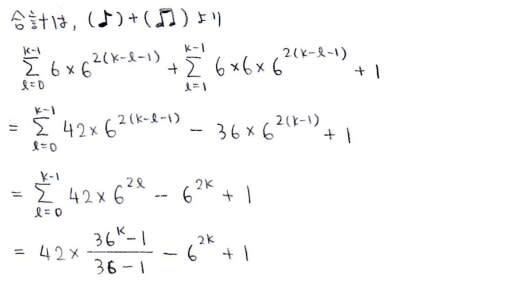

となり,前回までに求めた答えと一致しました


よく見ると1≦ℓ≦k-1みたいな条件式が途中入っていたのでk≧2での議論に
なってたぽいですがk=1でもこの結果は正しいですね。
お次はnが奇数の場合です~~



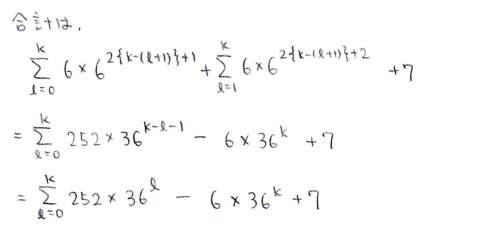
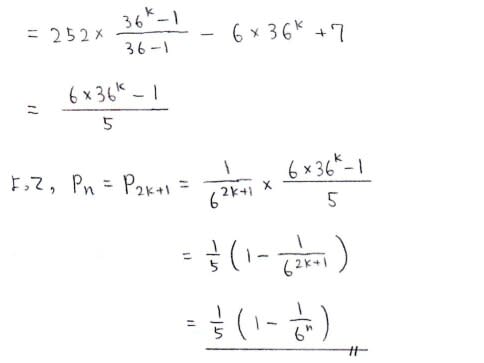
こちらも結果が一致しました

すべてのkに対して合ってます。
…というわけで,長々とした考察になりましたが無事に答えが導けました

しかしながら,そんな苦労しなくても前々回の最初にやったように,
漸化式立ててアッサリスッパリ解いちゃうことが出来ちゃうんですね~

とても面白い問題だったと思います














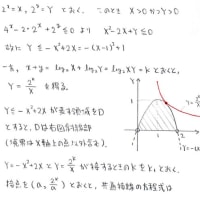
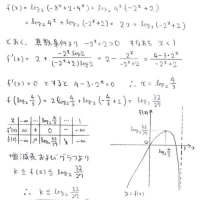
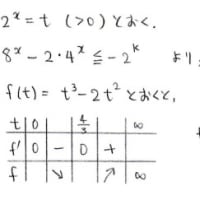


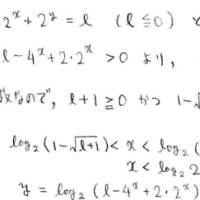

どうしてこんな解放が思い浮かぶのでしょうか
驚きを禁じえないです
また自分の実力のなさをひしひしと痛感しております
なかなか難しいやり方だったので
改めて読み返してみると,もっと丁寧に解説したほうが
分かりやすいなぁ~と思う箇所がいろいろありますね><
どうしてこんな解法が浮かぶのか
ということですが,この方法に関しては単純で,
確率の求め方の基本は,
(考えてる事象の場合の数)÷(全体の場合の数)
ですから,これに当てはめて解いてみたらどうなるだろう
というところが起点になりますね。
全体の場合の数は 6^n という分かりやすいものだし,
分子の方も,その気になれば計算できるに違いない!
むしろ計算出来ないわけがなかろう!
と思えるわけでして,次のステップは,
ではどうやって求めるかということになります。
きっと何らかのパターンのようなものがあるであろう
という思惑で p_2,p_3,p_4 あたりを考察してみると,
どういう規則性が潜んでいるかだんだん見えてきます。
特に連分数の性質に絡めて見ていくと
大体上で述べたような感じの話になっていったってわけですね~
確率漸化式を使って解くような確率の受験問題って
結構あるかと思うんですけど,そういう問題をシンプルに
(考えてる事象の場合の数)÷(全体の場合の数)
という発想で解こうとすると,概ね今回みたいに面倒くさくなります。
数学力鍛えるトレーニングとしてはなかなか良いですよ~
ただ,時間が無いとなかなか1題をじっくり考えてる余裕はないですけどね(;゜∇゜)
冬を迎えて,忙しい時期になっているかと思いますが
受験頑張ってくださいませ!
詳しく有り難うございます
今後もこちらのブログを参考にさせていただいて
頑張っていきたいです
受験数学の問題というのは様々な解法がある問題が多いです。
しかしながら問題集などの解答ページには,5つも6つも7つも別解載せてるわけにはいかないので,
普通はよりスタンダードなものを載せるかと思うんですが,
時に物足りない気分になることはありませんか?
こっちの解法のほうが美しいのに載ってない!とか
自分の解いた解法と違うんで自分の答案が満点なのかわからない!とか~
入試問題の解答を載せたり解説してるサイト,ブログは色々ありますが,
せっかくなのでちょっとでも差異を出してみようと思いまして
色んな方法で解いてみようという趣旨でやっております~
この記事みたいにちょっと難しいことをやってる場合もあるので,
なるべく堅さや難解さを緩めるために,ゆる~~いムードで
記事を作っているつもりです~
どこのサイトよりもじっくり問題を解いてみてるのに
どこのサイトよりもゆる~~い
そんな,まるで矛盾してるようなブログを目指しております。
参考になるかどうか分かりませんが
ゆる~い気持ちでたま~に覗いてみてくださいませ~♪