どもども。
昨日に引き続き今年の東北大入試理系数学大2問をやっていきます~
問題はこちら

前回:http://blog.goo.ne.jp/mathnegi/e/6b217d75454b3beb68540b11584adf5d
前回は(2)までやりましたんで,今回は(3)をやります~
(2)で求めた行列Bに対して,B^3=E(E:単位行列)となるようなmを求める問題です~
主な解答方針は大きく次の二分されるんじゃないでしょうか~
・ひたすら行列計算する
・回転行列の性質を利用する
前回も述べましたが,Bは実は回転行列になっているんですね~
それではまずは,最もシンプルな解法,
すなわちB^3を素直に求めるパターンをやってみましょう。

B^3は↑こんなのになります
この計算をするだけで結構大変です
しかもそのあとも更に大変です~~ッ

6次式の因数分解なんてウンザリですよね
①はとりあえず因数定理使って因数m-1を括りだすことは何とか出来るでしょう。
(m-1)^2を括りだすことで残りは4次式です。
その4次式は m^4+8m^3+18m^2+8m+1 です。
複2次式でもないので,この4次式の因数分解は難しそうですね~
注目するとすれば係数の対称性でしょうか
つまり係数の組が(1,8,18,8,1)となっていて,18を中心として左右対称です。
m^4+8m^3+18m^2+8m+1=m^2{(m^2+1/m^2)+8(m+1/m)+18}=m^2{(m+1/m)^2+8(m+1/m)+16}
おやおや,m+1/m=Xとおけばm^2(X+4)^2の形に変形できるではありませんか
そういうわけで因数分解が出来るちゅうわけですわ
あとは①の解を求めればいいです。
同じように②の解も求めて共通のものが答えです。
あるいは,①の解を②の左辺に代入して「=0」になるものが答え,としてもOKです。
ただし後者は計算がめんどくさくなるので②も解いちゃうのがいいでしょう
②のほうは因数m-1とm+1を括りだすとこまでは問題ないでしょう。
残った4次式は m^4-14m^2+1 です。複2次式ですのでm^2=Mとおいて
2次方程式M^2-14M+1=0を解いてしまいましょう
すると,M=7±4√3が出てきます~
ということは(M-7+4√3)(M-7-√3)と因数分解できますが,
m^2=M=7±4√3=(2±√3)^2
に注意すると
(M-7+4√3)(M-7-√3)=(m-2+√3)(m+2-√3)(m-2-√3)(m+2+√3)=(m^2-4m+1)(m^2+4m+1)
という因数分解が出来上がります
あとは共通解を列挙しておしまいですね♪
なんだかんだで面倒な計算と地味に頭を悩ます因数分解に苦しめられるので
あまりオススメできる解法ではないですね
同じB^3を求めるにしても,もう少し工夫して計算を楽に出来ないもんでしょうか
行列計算を手助けしてくれる強力なツールといえば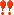
ケーリー・ハミルトンの定理

少しは扱いやすい??

最初の解法よりはだいぶ易しくなりました
もうちょい工夫してみましょ~
今の解法の後半なんですが,B=kEの形に変形できます。
B^3=k^3E=Eより,k^3=1を得ます


次はB^3=Eを(B-E)(B^2+B+E)=0と変形して解く解法を考えてみます
ただし大きな注意が必要です
(B-E)(B^2+B+E)=0であることから,B-E=0またはB^2+B+E=0とするのは誤りです
行列の積については「X=0またはY=0」という条件を満たしていないのにXY=0となることがあります 例えば
例えば
(1 0)(0 0)=0ですね


(0 0)(0 1)
XY=0ならば「X=0またはY=0またはdet(X)=det(Y)=0」
が正しいです
ただ,同値ではないです


det(X)=det(Y)=0だからといってXY=0とは限りません
そんなことに注意して問題を解いてみます~

②はケーリー・ハミルトンを使うと割と簡単です~

det(B-E)=det(B^2+B+E)=0を両方満たすことは出来ないようですね。
これで答えはm=1,-2±√3が得られました
②の計算をケーリー・ハミルトンを使わないでやってみます。
複素数を交えた別のやり方でいってみましょ







結構めんどいですね。
④とかで出てくる2次方程式は直接解くと更に面倒ですよ
試しに④を解いてみます~


ここまでは,B^3を直接求める方針でやっていましたが,
次は回転行列の性質を使って解いてみましょう
m=tan(θ/2)とおいてみます。よくやるおき方ですね。
このとき,cosθ=(1-m^2)/(1+m^2),sinθ=2m/(1+m^2)と書けます。
もはやこの式自体を公式のように覚えてしまってる人も多いでしょう
今回は角度を微妙にズラして, θ=φ+π/2 とおきます。
すると行列Bは原点中心,回転角度φの1次変換を表す行列になってることが分かります
B^3は回転角3φの1次変換を表す行列になるので,それがEと等しいということは
3φ=2π×k(k:整数)の形をしているということになります


はじめからいつもと違うおき方をして
cosθ=2m/(1+m^2),sinθ=(m^2-1)/(1+m^2)
とおいちゃうと,もうちょっと簡単になります

なお,cosθ=2m/(1+m^2),sinθ=(m^2-1)/(1+m^2) とおいた後,
3倍角の公式でcos3θ,sin3θを計算してcos3θ=1,sin3θ=0を解く,
という方針を立ててしまうと,一番最初のめんどくさい計算と変わらなくなってしまいます


ただ,直接的にガチンコでB^3を計算するよりは楽に計算できますね
(3)に関してはどのような解法を選択するかによって受験生の運命を左右しかねない,
そんな印象を持つ問題でした
昨日に引き続き今年の東北大入試理系数学大2問をやっていきます~

問題はこちら

前回:http://blog.goo.ne.jp/mathnegi/e/6b217d75454b3beb68540b11584adf5d
前回は(2)までやりましたんで,今回は(3)をやります~

(2)で求めた行列Bに対して,B^3=E(E:単位行列)となるようなmを求める問題です~

主な解答方針は大きく次の二分されるんじゃないでしょうか~
・ひたすら行列計算する
・回転行列の性質を利用する
前回も述べましたが,Bは実は回転行列になっているんですね~

それではまずは,最もシンプルな解法,
すなわちB^3を素直に求めるパターンをやってみましょう。

B^3は↑こんなのになります

この計算をするだけで結構大変です

しかもそのあとも更に大変です~~ッ


6次式の因数分解なんてウンザリですよね

①はとりあえず因数定理使って因数m-1を括りだすことは何とか出来るでしょう。
(m-1)^2を括りだすことで残りは4次式です。
その4次式は m^4+8m^3+18m^2+8m+1 です。
複2次式でもないので,この4次式の因数分解は難しそうですね~

注目するとすれば係数の対称性でしょうか

つまり係数の組が(1,8,18,8,1)となっていて,18を中心として左右対称です。
m^4+8m^3+18m^2+8m+1=m^2{(m^2+1/m^2)+8(m+1/m)+18}=m^2{(m+1/m)^2+8(m+1/m)+16}
おやおや,m+1/m=Xとおけばm^2(X+4)^2の形に変形できるではありませんか

そういうわけで因数分解が出来るちゅうわけですわ

あとは①の解を求めればいいです。
同じように②の解も求めて共通のものが答えです。
あるいは,①の解を②の左辺に代入して「=0」になるものが答え,としてもOKです。
ただし後者は計算がめんどくさくなるので②も解いちゃうのがいいでしょう

②のほうは因数m-1とm+1を括りだすとこまでは問題ないでしょう。
残った4次式は m^4-14m^2+1 です。複2次式ですのでm^2=Mとおいて
2次方程式M^2-14M+1=0を解いてしまいましょう

すると,M=7±4√3が出てきます~

ということは(M-7+4√3)(M-7-√3)と因数分解できますが,
m^2=M=7±4√3=(2±√3)^2
に注意すると
(M-7+4√3)(M-7-√3)=(m-2+√3)(m+2-√3)(m-2-√3)(m+2+√3)=(m^2-4m+1)(m^2+4m+1)
という因数分解が出来上がります

あとは共通解を列挙しておしまいですね♪
なんだかんだで面倒な計算と地味に頭を悩ます因数分解に苦しめられるので
あまりオススメできる解法ではないですね

同じB^3を求めるにしても,もう少し工夫して計算を楽に出来ないもんでしょうか

行列計算を手助けしてくれる強力なツールといえば
ケーリー・ハミルトンの定理


少しは扱いやすい??


最初の解法よりはだいぶ易しくなりました

もうちょい工夫してみましょ~

今の解法の後半なんですが,B=kEの形に変形できます。
B^3=k^3E=Eより,k^3=1を得ます



次はB^3=Eを(B-E)(B^2+B+E)=0と変形して解く解法を考えてみます

ただし大きな注意が必要です

(B-E)(B^2+B+E)=0であることから,B-E=0またはB^2+B+E=0とするのは誤りです

行列の積については「X=0またはY=0」という条件を満たしていないのにXY=0となることがあります
 例えば
例えば(1 0)(0 0)=0ですね



(0 0)(0 1)
XY=0ならば「X=0またはY=0またはdet(X)=det(Y)=0」
が正しいです

ただ,同値ではないです



det(X)=det(Y)=0だからといってXY=0とは限りません

そんなことに注意して問題を解いてみます~

②はケーリー・ハミルトンを使うと割と簡単です~

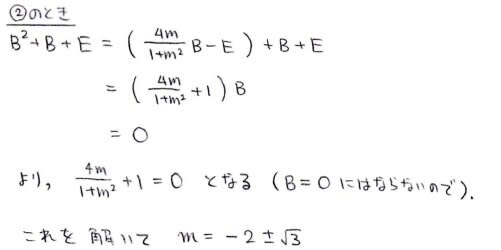

det(B-E)=det(B^2+B+E)=0を両方満たすことは出来ないようですね。
これで答えはm=1,-2±√3が得られました

②の計算をケーリー・ハミルトンを使わないでやってみます。
複素数を交えた別のやり方でいってみましょ








結構めんどいですね。
④とかで出てくる2次方程式は直接解くと更に面倒ですよ

試しに④を解いてみます~


ここまでは,B^3を直接求める方針でやっていましたが,
次は回転行列の性質を使って解いてみましょう

m=tan(θ/2)とおいてみます。よくやるおき方ですね。
このとき,cosθ=(1-m^2)/(1+m^2),sinθ=2m/(1+m^2)と書けます。
もはやこの式自体を公式のように覚えてしまってる人も多いでしょう

今回は角度を微妙にズラして, θ=φ+π/2 とおきます。
すると行列Bは原点中心,回転角度φの1次変換を表す行列になってることが分かります

B^3は回転角3φの1次変換を表す行列になるので,それがEと等しいということは
3φ=2π×k(k:整数)の形をしているということになります



はじめからいつもと違うおき方をして
cosθ=2m/(1+m^2),sinθ=(m^2-1)/(1+m^2)
とおいちゃうと,もうちょっと簡単になります


なお,cosθ=2m/(1+m^2),sinθ=(m^2-1)/(1+m^2) とおいた後,
3倍角の公式でcos3θ,sin3θを計算してcos3θ=1,sin3θ=0を解く,
という方針を立ててしまうと,一番最初のめんどくさい計算と変わらなくなってしまいます



ただ,直接的にガチンコでB^3を計算するよりは楽に計算できますね

(3)に関してはどのような解法を選択するかによって受験生の運命を左右しかねない,
そんな印象を持つ問題でした














 考え方1
考え方1



































 )ので,前回と同じ解法の順序でやっていってみましょう~
)ので,前回と同じ解法の順序でやっていってみましょう~ 考え方1
考え方1


 ,y=s+t-1……
,y=s+t-1……











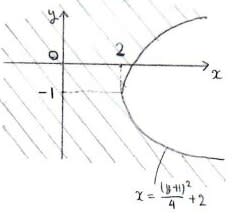













 という作戦です。
という作戦です。 といえますね。
といえますね。

 ,y=s-t-1……
,y=s-t-1……
 ,引けばx-y=2t+2……
,引けばx-y=2t+2……