どもども。
前回の続きで2012年長野県公立高校入試数学第4問の続きをやっていきます。
前回のはこちら
http://blog.goo.ne.jp/mathnegi/e/8ec6f1b22153305034fa128433f71b17
円やら相似やらが出てくる,幾何の問題でした。
後半戦の(2)2番と(3)を残していました。


 (2)2番
(2)2番
∠BAQ=90°,AB=3cm,AQ=9cmのときに円の直径を求めよ,
という問題です。
ABとAQの長さが分かっているので,1番で得たAB^2=AP×AQを
用いればAPの長さが分かります。
直角三角形ABPにおいて三平方の定理を使えばBPが求められます。
基本かつ重要ながら意外と見落としやすい点ですが,
∠BAP=90°であることからBPが円の直径であることが分かります

さて,今回も別解を考えてみましょう。簡単か面倒かは別として非常に
多くの解法が考えられる問題ではあります。
BP自体は△ABPか△BPCで三平方の定理使う解法が多そうですが,
AP,PC,BC辺りの長さを求める手法は多岐に渡ります。
AP=a,PC=hとおいてみます。
また,AからBCに垂線AHを下しておきます。

利用できそうな条件が沢山あります。
AH⊥BQ AH//PC AP:PQ=HC:CQ
BO:OP=BH:HC AH:PC=AQ:PQ=HQ:CQ
BH=HC OA=OB=OP
△ABP∽△AQB∽△CQP∽△HAB
他にも方ベキの定理,メネラウスの定理,トレミーの定理や
面積の関係式なんかも使えそうです。
全部やってたらキリがないので,2,3挙げるにとどめておきます
AHの長さは面積の関係式から直ちに求めることも出来ます。

△ABH∽△QBAの関係式を使うとBHもあっさり求められます。
あるいは直角三角形ABHで三平方とか。

AH,BHの長さが分かっていれば,最後は相似関係でフィニッシュも
できますね。
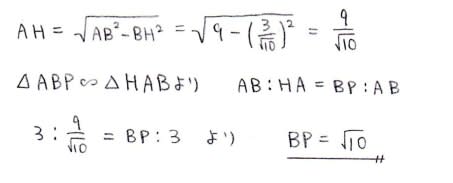
続いてはaを求める方法を幾つか挙げてみます。
まずはAP:PQ=a:(9-a)よりBH:HC:CQ=a:a:(9-a)
になる事や,面積の関係式を用いてaを求めてみるやり方です。

次は△OBHにおいてOB^2=OH^2+BH^2で立式しています。

上で使ってるBH=(3√10a)/(a+9)と合わせて,(3√10a)/(a+9)=3/√10
を解いてa=1を求めるというのも良いですね
あるいは辺の比などの関係式などと合わせるのも良さそうです。
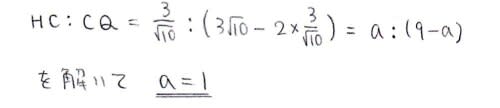
まだまだ色々ありますが,これくらいにして~
といいつつ一応,高校数学の三角比を用いた解法も1個挙げときますか。

外接円絡みなので正弦定理なんかも使えますね
 (3)
(3)
今度は△ABCが正三角形の場合です。ころころ状況が変わっていくので
受験生にとっては迷惑な話です。無駄に問題数が多いような錯覚をしてしまうかもしれません

さて,60°の角がいっぱいあります。△ABCの各角と円周角の定理から
導かれる∠APB,∠BPC。見落としやすいですが∠CPQもまた60°に
なっています。さらにいうと∠ACQ=120°です。
2角相等によって相似が導かれる(2)までとは違う三角形が幾つかあります。

恐らくはこれらの相似関係を利用して解くのが出題側の考える模範解答かと思います。

この問題も非常に解法パターンは沢山考えられる問題です。
上記解答の後半は例えばCQを求めてBCと足すという方針でもOKです。

ℓを求めるのには例えば△PAC∽△CAQより導かれる
CA:AQ=AP:ACから ℓ:7=4:ℓ
として求めるのもいいですね。
この問題ではPB=6cm,PQ=3cm,PC=2cmが与えられていますが,
実はPB=6cm,PQ=3cmの時点で図が一意的に定まっていて,
PC=2cmという情報は必要ありません

従って,無くても解けるのですがわざわざ親切に付記してくれたのは
上で述べたような相似関係を用いた解法を使うことを主に想定しているからだと思います。
PC=2cmを知らない状態で△PBQと△PACの相似比が3:2で
あることを導くには,例えばPCが∠BPQの2等分線であることを利用する
作戦とかがあります。
角の2等分線と線分比の関係は中学生なら知ってる人は必ずしも多くはないかもしれませんが,
BC:CQ=PB:PQ=2:1が成り立ちます。
これによりBQ=(3/2)ℓになるので,△PBQと△PACの相似比は
BQ:AC=3:2となります
ここでPC=2cmを一切使わないでBQを求める解法を挙げてみます。

AとBからそれぞれ垂線AHとBIを引いてみます。
いま使うのはBIのほうです。
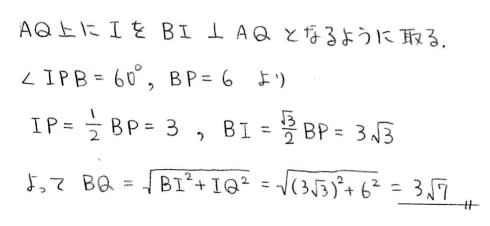
あっさりやっつけてしまいました
図形をはみ出した補助線を使って,Qから直線BP上に垂線QJを下ろして
△PJQに着目する手もありますね。
次はAHを利用してℓを求めてみます。
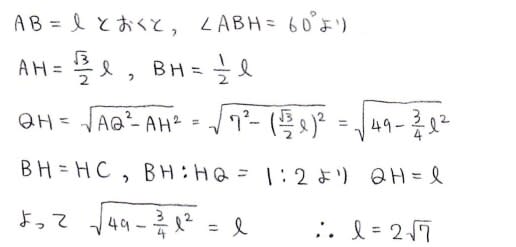
さて,AP=4cmは,トレミーの定理なんかを使ってもすぐ得られます。
ややマイナーな定理ですが,結構役立つ定理なんで自分は大好きです

次はメネラウスの定理と方ベキの定理を使ってACを求めてみます。

さっきの問題と同様に三角比を用いた解法も挙げてみます。
一例として△PBQで正弦定理を使ってみました。

最後にちょっと大掛かりな解法を挙げてみます。
図を見れば分かると思いますが,△PACは△PBQを点Pを中心に
60°回転移動したあと点Pを中心に2/3倍に縮小したものになっています
そこで縮小せずに回転移動だけしたものを△PB'Q'とおいてみますね。

回転角が60°なので△PQQ'と△PBB'はそれぞれ1辺3cm,6cmの
正三角形になっています。BQ=B'Q'なのでB'Q'の長さを求めれば
OKです。
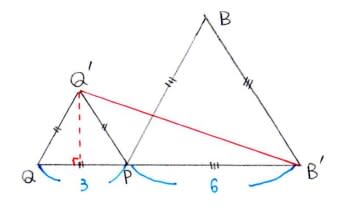
上図のように,2つの正三角形が隣り合っていてる図形を考えて
B'とQ'を結んでその長さを求めよ,というシンプルな問題に還元されました。これを求めるのは容易です。

BとQを結んでBQを求めてるのが少し上に挙げたPC=2cmを利用せずに
さくっと解いた解法に相当します。もちろんそっちの方が簡単です。
この問題では無駄に大掛かりになっていますが,
よく分からない難しい補助線をあれこれ引かなきゃいけない図形の問題(ラングレーの問題とか)なんかでは
回転移動の発想は意外と有効だったりします。正三角形や直角二等辺三角形とかを
作り出すのに便利だし!
前回の続きで2012年長野県公立高校入試数学第4問の続きをやっていきます。
前回のはこちら
http://blog.goo.ne.jp/mathnegi/e/8ec6f1b22153305034fa128433f71b17
円やら相似やらが出てくる,幾何の問題でした。
後半戦の(2)2番と(3)を残していました。


 (2)2番
(2)2番∠BAQ=90°,AB=3cm,AQ=9cmのときに円の直径を求めよ,
という問題です。
ABとAQの長さが分かっているので,1番で得たAB^2=AP×AQを
用いればAPの長さが分かります。
直角三角形ABPにおいて三平方の定理を使えばBPが求められます。
基本かつ重要ながら意外と見落としやすい点ですが,
∠BAP=90°であることからBPが円の直径であることが分かります


さて,今回も別解を考えてみましょう。簡単か面倒かは別として非常に
多くの解法が考えられる問題ではあります。
BP自体は△ABPか△BPCで三平方の定理使う解法が多そうですが,
AP,PC,BC辺りの長さを求める手法は多岐に渡ります。
AP=a,PC=hとおいてみます。
また,AからBCに垂線AHを下しておきます。

利用できそうな条件が沢山あります。
AH⊥BQ AH//PC AP:PQ=HC:CQ
BO:OP=BH:HC AH:PC=AQ:PQ=HQ:CQ
BH=HC OA=OB=OP
△ABP∽△AQB∽△CQP∽△HAB
他にも方ベキの定理,メネラウスの定理,トレミーの定理や
面積の関係式なんかも使えそうです。
全部やってたらキリがないので,2,3挙げるにとどめておきます

AHの長さは面積の関係式から直ちに求めることも出来ます。

△ABH∽△QBAの関係式を使うとBHもあっさり求められます。
あるいは直角三角形ABHで三平方とか。

AH,BHの長さが分かっていれば,最後は相似関係でフィニッシュも
できますね。
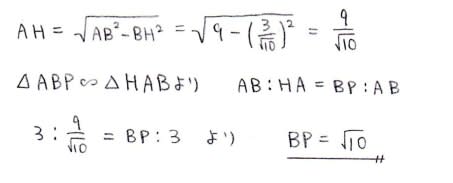
続いてはaを求める方法を幾つか挙げてみます。
まずはAP:PQ=a:(9-a)よりBH:HC:CQ=a:a:(9-a)
になる事や,面積の関係式を用いてaを求めてみるやり方です。

次は△OBHにおいてOB^2=OH^2+BH^2で立式しています。

上で使ってるBH=(3√10a)/(a+9)と合わせて,(3√10a)/(a+9)=3/√10
を解いてa=1を求めるというのも良いですね

あるいは辺の比などの関係式などと合わせるのも良さそうです。
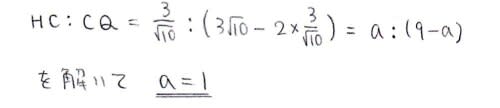
まだまだ色々ありますが,これくらいにして~
といいつつ一応,高校数学の三角比を用いた解法も1個挙げときますか。

外接円絡みなので正弦定理なんかも使えますね

 (3)
(3)今度は△ABCが正三角形の場合です。ころころ状況が変わっていくので
受験生にとっては迷惑な話です。無駄に問題数が多いような錯覚をしてしまうかもしれません


さて,60°の角がいっぱいあります。△ABCの各角と円周角の定理から
導かれる∠APB,∠BPC。見落としやすいですが∠CPQもまた60°に
なっています。さらにいうと∠ACQ=120°です。
2角相等によって相似が導かれる(2)までとは違う三角形が幾つかあります。

恐らくはこれらの相似関係を利用して解くのが出題側の考える模範解答かと思います。

この問題も非常に解法パターンは沢山考えられる問題です。
上記解答の後半は例えばCQを求めてBCと足すという方針でもOKです。

ℓを求めるのには例えば△PAC∽△CAQより導かれる
CA:AQ=AP:ACから ℓ:7=4:ℓ
として求めるのもいいですね。
この問題ではPB=6cm,PQ=3cm,PC=2cmが与えられていますが,
実はPB=6cm,PQ=3cmの時点で図が一意的に定まっていて,
PC=2cmという情報は必要ありません


従って,無くても解けるのですがわざわざ親切に付記してくれたのは
上で述べたような相似関係を用いた解法を使うことを主に想定しているからだと思います。
PC=2cmを知らない状態で△PBQと△PACの相似比が3:2で
あることを導くには,例えばPCが∠BPQの2等分線であることを利用する
作戦とかがあります。
角の2等分線と線分比の関係は中学生なら知ってる人は必ずしも多くはないかもしれませんが,
BC:CQ=PB:PQ=2:1が成り立ちます。
これによりBQ=(3/2)ℓになるので,△PBQと△PACの相似比は
BQ:AC=3:2となります

ここでPC=2cmを一切使わないでBQを求める解法を挙げてみます。

AとBからそれぞれ垂線AHとBIを引いてみます。
いま使うのはBIのほうです。
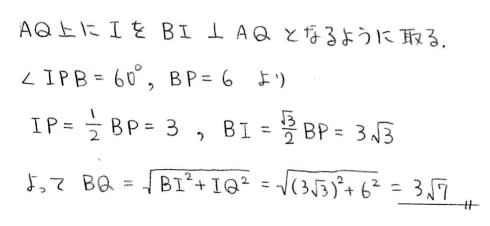
あっさりやっつけてしまいました

図形をはみ出した補助線を使って,Qから直線BP上に垂線QJを下ろして
△PJQに着目する手もありますね。
次はAHを利用してℓを求めてみます。
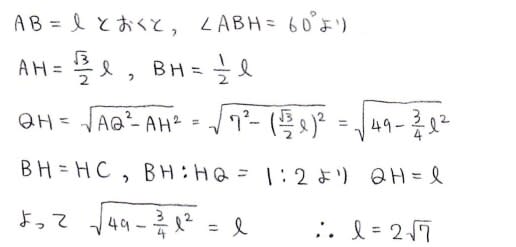
さて,AP=4cmは,トレミーの定理なんかを使ってもすぐ得られます。
ややマイナーな定理ですが,結構役立つ定理なんで自分は大好きです


次はメネラウスの定理と方ベキの定理を使ってACを求めてみます。

さっきの問題と同様に三角比を用いた解法も挙げてみます。
一例として△PBQで正弦定理を使ってみました。

最後にちょっと大掛かりな解法を挙げてみます。
図を見れば分かると思いますが,△PACは△PBQを点Pを中心に
60°回転移動したあと点Pを中心に2/3倍に縮小したものになっています

そこで縮小せずに回転移動だけしたものを△PB'Q'とおいてみますね。

回転角が60°なので△PQQ'と△PBB'はそれぞれ1辺3cm,6cmの
正三角形になっています。BQ=B'Q'なのでB'Q'の長さを求めれば
OKです。

上図のように,2つの正三角形が隣り合っていてる図形を考えて
B'とQ'を結んでその長さを求めよ,というシンプルな問題に還元されました。これを求めるのは容易です。

BとQを結んでBQを求めてるのが少し上に挙げたPC=2cmを利用せずに
さくっと解いた解法に相当します。もちろんそっちの方が簡単です。
この問題では無駄に大掛かりになっていますが,
よく分からない難しい補助線をあれこれ引かなきゃいけない図形の問題(ラングレーの問題とか)なんかでは
回転移動の発想は意外と有効だったりします。正三角形や直角二等辺三角形とかを
作り出すのに便利だし!

































 めでたしめでたし
めでたしめでたし










 (1)1番
(1)1番








