どもども。
しばらく今年の東大入試理系数学を解いてきましたが,いよいよラストです。
今回は第6問をやります
問題はこちら
http://www.yozemi.ac.jp/nyushi/sokuho/recent/tokyo/zenki/sugaku_ri/mon6.html
第5問に続いて行列がらみの出題です。
見た瞬間に「うわッ 」と気が滅入るような
」と気が滅入るような
何がなんだかよく分からない,とにかく計算の面倒臭そうなf(x)が目に入ります。
腕力勝負といった感じでしょうか。
しかしまぁ,計算がしんどいという点を除けば,
決して難しい問題ではないですコレ。
いかに要領よく解くかが試される感じかな?
でもどんな工夫してもそれなりに計算量はあるような気はしますが~
まずは(1)です。f(x)の最大値を求めよ!
ということでf(x)を分かりやすい形に直してやるところから始めましょう。
最初に U(t)AU(-t)-B を計算します。
なんなんだ!このオマケのBは!余計な項をつけるなんて!
…なーんて,思うわけですが,実は計算結果をスッキリさせてくれる手助けを
してくれる項でした
厄介なので U(t)AU(-t) だけ計算してBは放置しておこう!という方針を取ると損します
U(t)AU(-t)-B は変数xを含んでいないのでいわば定数のようなもの。
これをとりあえずWなどとおいて,その成分もp,q,r,sなどとでもおいておきます。
次は U(x)(1 0)U(-x) を計算します。
(0 -1)
これはさっきの U(t)AU(-t) に近い形をしてるのですぐ計算できます。
tをxに置き換えて,a=1,b=-1としてやればいいんですね。
ここまでくると大分f(x)もシンプルな形になりました。
あとは最大値を求めるだけです。
どうやら三角関数の合成が使えそうです。


上の解法では合成の際に未知の角θが出てきましたが,
実際にそれを求めてもよいです。そんな解法がこちら。
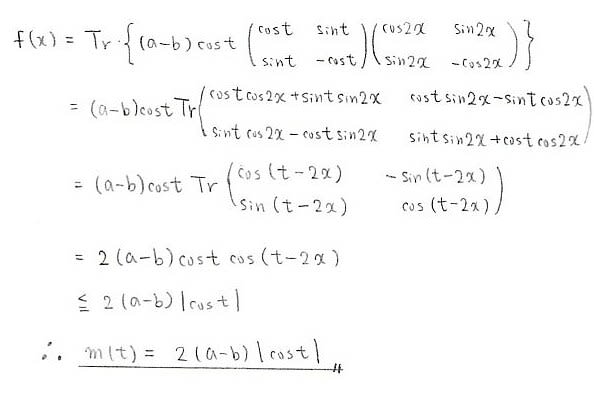
次はちょっと特殊なことをやってみます
関数f(x)は行列のトレース(対角成分の和)を用いて定義されているので
折角なので行列のトレースの性質を使って考えてみます。
2つの(2×2)-行列M_1,M_2が与えられたとき,Tr(M_1M_2)=Tr(M_2M_1)が成り立ちます。

また,Tr(M_1+M_2)=Tr(M_1)+Tr(M_2)も成り立つこともすぐ確かめられるでしょう。
ついでにU(x)という行列は角度xの回転行列であることにも注目です。
つまり U(x)U(y)=U(x+y) が成り立ちます。
そんなあたりの話を駆使して計算してみた場合の解法です

後半の項は今の最後の計算でaとbを逆にして角度をt-xからxに置き換えれば
計算結果が得られます。

次は(2)をみてみましょう。
(1)でも骨の折れる計算をしたのにまた厄介そうな計算が待っていました。
骨だけでなく心も折れそうです
まずは挫けずに 2Tr{U(t)CU(-t)D} と Tr{U(t)AU(-t)+B}-m(t) を計算します。
それによって証明すべき不等式をもう少し明瞭化してみます。
(cost)^2=|cost|^2 に注意です。両辺が|cost|で割れます。

さて後半です。指数のcとか1-cというのがなんだか煩わしいです。
すごい複雑な評価とかしなきゃいけないのかしら?と思いきや
b^c≦a^c と b^(1-c)≦a^(1-c) を使ってaの累乗を評価しちゃうだけで
キレイにうまくいっちゃうのでした。

それとは別に,相加平均と相乗平均の関係を用いてもうまくいきます。

|cost|=XとおいてXの2次関数または1次関数を考えてもOKです。
両辺を|cost|で割る前の不等式を2次関数を使って証明したのがコレ。

最後に,証明すべき不等式を
m(t)≧Tr{U(t)AU(-t)-B}-2Tr{U(t)CU(-t)D-B}
と変形してみた場合の解答を挙げてみます。
(1)で U(t)AU(-t)-B は既に計算してあります。
しかもよく見ると Tr{U(t)AU(-t)-B}=0 なんですね
結局,m(t)≧-2Tr{U(t)CU(-t)D-B}
を証明することに帰着します。

しばらく今年の東大入試理系数学を解いてきましたが,いよいよラストです。
今回は第6問をやります

問題はこちら
http://www.yozemi.ac.jp/nyushi/sokuho/recent/tokyo/zenki/sugaku_ri/mon6.html
第5問に続いて行列がらみの出題です。
見た瞬間に「うわッ
 」と気が滅入るような
」と気が滅入るような何がなんだかよく分からない,とにかく計算の面倒臭そうなf(x)が目に入ります。
腕力勝負といった感じでしょうか。
しかしまぁ,計算がしんどいという点を除けば,
決して難しい問題ではないですコレ。
いかに要領よく解くかが試される感じかな?
でもどんな工夫してもそれなりに計算量はあるような気はしますが~

まずは(1)です。f(x)の最大値を求めよ!
ということでf(x)を分かりやすい形に直してやるところから始めましょう。
最初に U(t)AU(-t)-B を計算します。
なんなんだ!このオマケのBは!余計な項をつけるなんて!
…なーんて,思うわけですが,実は計算結果をスッキリさせてくれる手助けを
してくれる項でした

厄介なので U(t)AU(-t) だけ計算してBは放置しておこう!という方針を取ると損します
U(t)AU(-t)-B は変数xを含んでいないのでいわば定数のようなもの。
これをとりあえずWなどとおいて,その成分もp,q,r,sなどとでもおいておきます。
次は U(x)(1 0)U(-x) を計算します。
(0 -1)
これはさっきの U(t)AU(-t) に近い形をしてるのですぐ計算できます。
tをxに置き換えて,a=1,b=-1としてやればいいんですね。
ここまでくると大分f(x)もシンプルな形になりました。
あとは最大値を求めるだけです。
どうやら三角関数の合成が使えそうです。


上の解法では合成の際に未知の角θが出てきましたが,
実際にそれを求めてもよいです。そんな解法がこちら。
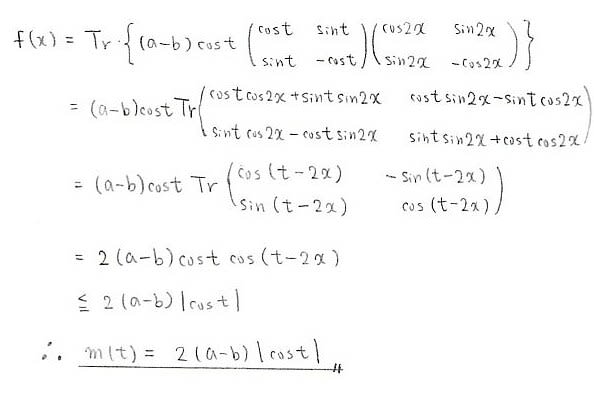
次はちょっと特殊なことをやってみます

関数f(x)は行列のトレース(対角成分の和)を用いて定義されているので
折角なので行列のトレースの性質を使って考えてみます。
2つの(2×2)-行列M_1,M_2が与えられたとき,Tr(M_1M_2)=Tr(M_2M_1)が成り立ちます。

また,Tr(M_1+M_2)=Tr(M_1)+Tr(M_2)も成り立つこともすぐ確かめられるでしょう。
ついでにU(x)という行列は角度xの回転行列であることにも注目です。
つまり U(x)U(y)=U(x+y) が成り立ちます。
そんなあたりの話を駆使して計算してみた場合の解法です


後半の項は今の最後の計算でaとbを逆にして角度をt-xからxに置き換えれば
計算結果が得られます。

次は(2)をみてみましょう。
(1)でも骨の折れる計算をしたのにまた厄介そうな計算が待っていました。
骨だけでなく心も折れそうです

まずは挫けずに 2Tr{U(t)CU(-t)D} と Tr{U(t)AU(-t)+B}-m(t) を計算します。
それによって証明すべき不等式をもう少し明瞭化してみます。
(cost)^2=|cost|^2 に注意です。両辺が|cost|で割れます。

さて後半です。指数のcとか1-cというのがなんだか煩わしいです。
すごい複雑な評価とかしなきゃいけないのかしら?と思いきや
b^c≦a^c と b^(1-c)≦a^(1-c) を使ってaの累乗を評価しちゃうだけで
キレイにうまくいっちゃうのでした。

それとは別に,相加平均と相乗平均の関係を用いてもうまくいきます。

|cost|=XとおいてXの2次関数または1次関数を考えてもOKです。
両辺を|cost|で割る前の不等式を2次関数を使って証明したのがコレ。

最後に,証明すべき不等式を
m(t)≧Tr{U(t)AU(-t)-B}-2Tr{U(t)CU(-t)D-B}
と変形してみた場合の解答を挙げてみます。
(1)で U(t)AU(-t)-B は既に計算してあります。
しかもよく見ると Tr{U(t)AU(-t)-B}=0 なんですね

結局,m(t)≧-2Tr{U(t)CU(-t)D-B}
を証明することに帰着します。





















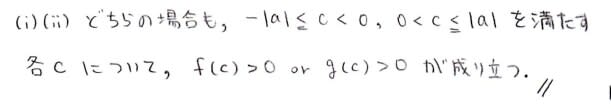








 ということを証明してくれという問題です。
ということを証明してくれという問題です。