どもども。
本日は2012年東大入試理系数学第4問を取り上げます
問題はこちら
http://www.yozemi.ac.jp/nyushi/sokuho/recent/tokyo/zenki/sugaku_ri/mon4.html
整数に関する論証問題です。
今年の問題セットの中では一番難しかったとされる問題です。
(1),(2),共に「連続2自然数は互いに素である」という性質がポイントになっていて,それに気付くかどうかが勝負の分かれ目になっています。
また,問題文は(1),(2)とも似ているのですが,(1)を利用して(2)を解くという
タイプの問題ではないようです。どうやって(1)を使うんだろうという点に固執しちゃうと(2)は苦戦するかもしれません。
というわけで,まずは今回の問題のキモになる「連続2自然数は互いに素である」ことを確認しておきましょう。例えば8と9は互いに素です。8の正の約数は2だけです。偶数と奇数は交互に表れるので9が偶数になることはありません。また,9の正の約数は3だけです。3の倍数は2個おきに現れるので8は3の倍数ではありません。一般にp≧2のとき,pの倍数は(p-1)個おきに現れるので,かなり荒く分布していますね。だからpの倍数が隣り合うなんてことは無いわけです。

この「連続2自然数は互いに素である」という性質は,
試験では特に断りなく用いても良いかと思います。
連続2自然数の積N(N+1)をk^nと等しいとおいてみると,
実はNもN+1もn乗数でなければならないという事実にぶち当たります。
しかしながら,n乗数というのもなかなか荒い分布をしていて,
例えば2乗数ですら 1 4 9 16 25 36 49 64 81 100 121 …
という隙間だらけの分布になっています。
よってn乗数が隣り合うなんてことはおかしいぞ
というネタで矛盾を導きます

ただ,この「互いに素」の性質が非常に本質的であるため
これを用いない別解というものがなかなか見当たりません。
何か本質的な別解法があったら是非教えてほしいところです
N(N+1)=k^n をNの2次方程式と思うと,その判別式として1+4k^nが出てきます。これが平方数になるための条件を考えるというアプローチが例えば考えられます。
nが偶数の場合は簡単に矛盾が引き出せます。

一方でnが奇数の場合は難しいようです。1+4k^n=(2m-1)^2などとおいて整理すると結局元の命題に戻ってしまいます
何か面白い別解は無いもんですかね~
続いて(2)です。
連続n自然数の積N(N+1)(N+2)×…×(N+n-1)がk^nと書けるとすれば,
kはこの連続n自然数の相乗平均です。
さて,N(N+1)(N+2)×…×(N+n-1)は一番小さい整数Nをn回掛けた積N^nよりも
当然大きいです。そして一番大きい整数N+n-1をn回掛けた積(N+n-1)^nよりも
小さいです。このことから,N^n<k^n<(N+n-1)^nという評価が得られます。
従って,N<k<N+n-1であり,kの値の候補は絞られてしまいます。
n=2のときは,N<k<N+1となりますが,NとN+1の間に自然数はありません。
この時点でもう矛盾を生じています。
n≧3のときは,kはN+1,N+2,…,N+n-2の中のどれかという事になります。
このとき「連続2自然数は互いに素である」という性質から,kはk+1の倍数ではありませんし,k^nもやはりk+1の倍数ではありません。
しかし N(N+1)(N+2)×…×(N+n-1)=k^n の表示からk^nがk+1の倍数であることが言えてしまいます。これが矛盾です

n=2の場合とn≧3の場合とを分けなければならないのが忘れやすいところだと思います。
また,もう1つ気を付けたいのは,自然数kに対し,
「kとk+1は互いに素」という性質を使うか「kとk-1は互いに素」という性質を
使うかによって微妙に議論に差異が生じることです。
上記解答では「k^nはk+1の倍数ではない」という話を用いてますが,
一方で「k^nはk-1の倍数ではない」というのは必ずしも正しくありません。
k=2のときは2^nは1の倍数ですからね
なので途中からやり直しましょう~。

この問題も何か本質的に別の解法というものは何か無いもんですかね
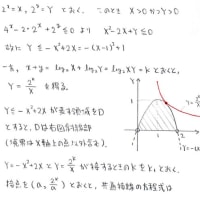
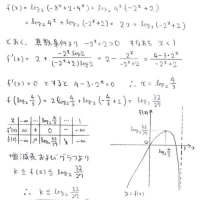
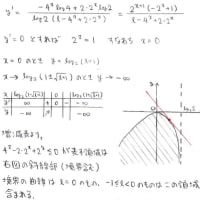
n=3,4の場合は次のような解法があります。

一般のnに関しても同様に(n-1)次方程式を解いてそれの解が自然数にならない
ことを言えばいいんでしょうが,「互いに素」の性質を使わないとなると
なかなか大変そうです。
本日は2012年東大入試理系数学第4問を取り上げます

問題はこちら
http://www.yozemi.ac.jp/nyushi/sokuho/recent/tokyo/zenki/sugaku_ri/mon4.html
整数に関する論証問題です。
今年の問題セットの中では一番難しかったとされる問題です。
(1),(2),共に「連続2自然数は互いに素である」という性質がポイントになっていて,それに気付くかどうかが勝負の分かれ目になっています。
また,問題文は(1),(2)とも似ているのですが,(1)を利用して(2)を解くという
タイプの問題ではないようです。どうやって(1)を使うんだろうという点に固執しちゃうと(2)は苦戦するかもしれません。
というわけで,まずは今回の問題のキモになる「連続2自然数は互いに素である」ことを確認しておきましょう。例えば8と9は互いに素です。8の正の約数は2だけです。偶数と奇数は交互に表れるので9が偶数になることはありません。また,9の正の約数は3だけです。3の倍数は2個おきに現れるので8は3の倍数ではありません。一般にp≧2のとき,pの倍数は(p-1)個おきに現れるので,かなり荒く分布していますね。だからpの倍数が隣り合うなんてことは無いわけです。

この「連続2自然数は互いに素である」という性質は,
試験では特に断りなく用いても良いかと思います。
連続2自然数の積N(N+1)をk^nと等しいとおいてみると,
実はNもN+1もn乗数でなければならないという事実にぶち当たります。
しかしながら,n乗数というのもなかなか荒い分布をしていて,
例えば2乗数ですら 1 4 9 16 25 36 49 64 81 100 121 …
という隙間だらけの分布になっています。
よってn乗数が隣り合うなんてことはおかしいぞ
というネタで矛盾を導きます


ただ,この「互いに素」の性質が非常に本質的であるため
これを用いない別解というものがなかなか見当たりません。
何か本質的な別解法があったら是非教えてほしいところです

N(N+1)=k^n をNの2次方程式と思うと,その判別式として1+4k^nが出てきます。これが平方数になるための条件を考えるというアプローチが例えば考えられます。
nが偶数の場合は簡単に矛盾が引き出せます。

一方でnが奇数の場合は難しいようです。1+4k^n=(2m-1)^2などとおいて整理すると結局元の命題に戻ってしまいます

何か面白い別解は無いもんですかね~

続いて(2)です。
連続n自然数の積N(N+1)(N+2)×…×(N+n-1)がk^nと書けるとすれば,
kはこの連続n自然数の相乗平均です。
さて,N(N+1)(N+2)×…×(N+n-1)は一番小さい整数Nをn回掛けた積N^nよりも
当然大きいです。そして一番大きい整数N+n-1をn回掛けた積(N+n-1)^nよりも
小さいです。このことから,N^n<k^n<(N+n-1)^nという評価が得られます。
従って,N<k<N+n-1であり,kの値の候補は絞られてしまいます。
n=2のときは,N<k<N+1となりますが,NとN+1の間に自然数はありません。
この時点でもう矛盾を生じています。
n≧3のときは,kはN+1,N+2,…,N+n-2の中のどれかという事になります。
このとき「連続2自然数は互いに素である」という性質から,kはk+1の倍数ではありませんし,k^nもやはりk+1の倍数ではありません。
しかし N(N+1)(N+2)×…×(N+n-1)=k^n の表示からk^nがk+1の倍数であることが言えてしまいます。これが矛盾です


n=2の場合とn≧3の場合とを分けなければならないのが忘れやすいところだと思います。
また,もう1つ気を付けたいのは,自然数kに対し,
「kとk+1は互いに素」という性質を使うか「kとk-1は互いに素」という性質を
使うかによって微妙に議論に差異が生じることです。
上記解答では「k^nはk+1の倍数ではない」という話を用いてますが,
一方で「k^nはk-1の倍数ではない」というのは必ずしも正しくありません。
k=2のときは2^nは1の倍数ですからね

なので途中からやり直しましょう~。

この問題も何か本質的に別の解法というものは何か無いもんですかね

n=3,4の場合は次のような解法があります。

一般のnに関しても同様に(n-1)次方程式を解いてそれの解が自然数にならない
ことを言えばいいんでしょうが,「互いに素」の性質を使わないとなると
なかなか大変そうです。












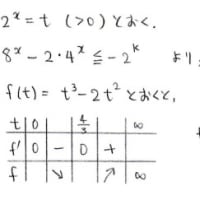


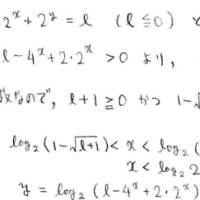

※コメント投稿者のブログIDはブログ作成者のみに通知されます