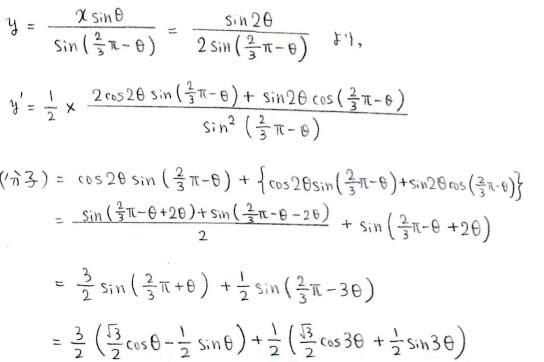どもども。
今回は今年の東北大入試(後期)理系数学第1問の(2)をやっていきます~
問題はこちら

前々回:http://blog.goo.ne.jp/mathnegi/e/fab5be206484546f5b690be5269a4275
前回:http://blog.goo.ne.jp/mathnegi/e/d0512f3c3bb938617512fb0ce731a08d
(2)は(1)と直接の関連性はないので,前回までのことは一旦置いておいてOKです
解法パターンは色々ありそうですがかかる手間は大差は無さそうです。
色々あるといっても,変数変換するかしないかという選択だと思いますが
 4^x-2・2^x+2^y≦0が表す領域を考える解法
4^x-2・2^x+2^y≦0が表す領域を考える解法
前回やった話と同じようなやり方をします
4^x-2・2^x+2^y=ℓ(ℓ≦0)が表す曲線のグラフを考え,ℓを動かしたときにどのような範囲を動くかを考察し
4^x-2・2^x+2^y≦0が表す領域Dをまず求めます


境界は上に凸な曲線で,ℓ=0のときの曲線に対応しています。
これと直線x+y=kが共有点を持つようなkの値の範囲を求めます。
領域と接するときのkをk_1とおけば,k≦k_1が求める答えです

 yを消去する解法その1
yを消去する解法その1
x+y=kとおくと,y=k-xになるので,これを代入することで
yを消去して考えることが出来ます

まずはこの左辺をf(x)とおく解法を見てみます

 yを消去する解法その2
yを消去する解法その2
指数関数のグラフより多項式のほうが考察はしやすい!
というわけで上と同じやり方で途中で2^x=tとおいてtの3次関数に帰着してみます


 yを消去する解法その3
yを消去する解法その3
今度は条件式をk≦f(x)の形に直してみます
こうすると,y=f(x)のグラフと直線y=kが交点を持つ条件に帰着します。

2^x=tなどとおいてみてもOKですよ~
 2^x=X,2^y=Yとおいてみる解法
2^x=X,2^y=Yとおいてみる解法
次は変数変換を使って解きます
(1)では多くの人が変数変換を使ったと思うので,恐らく(2)でも同じように変換した人が多いのではないかと思います
(1)と違って変数変換したからといって劇的に楽になるわけではないようです~



共通接線を求めるやり方としては,今回は次のような手も使えます


今回は今年の東北大入試(後期)理系数学第1問の(2)をやっていきます~

問題はこちら


前々回:http://blog.goo.ne.jp/mathnegi/e/fab5be206484546f5b690be5269a4275
前回:http://blog.goo.ne.jp/mathnegi/e/d0512f3c3bb938617512fb0ce731a08d
(2)は(1)と直接の関連性はないので,前回までのことは一旦置いておいてOKです

解法パターンは色々ありそうですがかかる手間は大差は無さそうです。
色々あるといっても,変数変換するかしないかという選択だと思いますが

 4^x-2・2^x+2^y≦0が表す領域を考える解法
4^x-2・2^x+2^y≦0が表す領域を考える解法前回やった話と同じようなやり方をします

4^x-2・2^x+2^y=ℓ(ℓ≦0)が表す曲線のグラフを考え,ℓを動かしたときにどのような範囲を動くかを考察し
4^x-2・2^x+2^y≦0が表す領域Dをまず求めます



境界は上に凸な曲線で,ℓ=0のときの曲線に対応しています。
これと直線x+y=kが共有点を持つようなkの値の範囲を求めます。
領域と接するときのkをk_1とおけば,k≦k_1が求める答えです


 yを消去する解法その1
yを消去する解法その1x+y=kとおくと,y=k-xになるので,これを代入することで
yを消去して考えることが出来ます


まずはこの左辺をf(x)とおく解法を見てみます


 yを消去する解法その2
yを消去する解法その2指数関数のグラフより多項式のほうが考察はしやすい!
というわけで上と同じやり方で途中で2^x=tとおいてtの3次関数に帰着してみます



 yを消去する解法その3
yを消去する解法その3今度は条件式をk≦f(x)の形に直してみます

こうすると,y=f(x)のグラフと直線y=kが交点を持つ条件に帰着します。

2^x=tなどとおいてみてもOKですよ~

 2^x=X,2^y=Yとおいてみる解法
2^x=X,2^y=Yとおいてみる解法次は変数変換を使って解きます

(1)では多くの人が変数変換を使ったと思うので,恐らく(2)でも同じように変換した人が多いのではないかと思います

(1)と違って変数変換したからといって劇的に楽になるわけではないようです~



共通接線を求めるやり方としては,今回は次のような手も使えます




















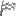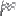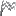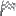

 )の形をしていますが
)の形をしていますが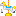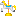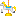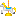
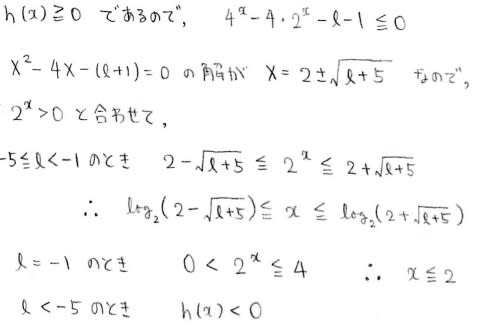




































 という予感はプンプンしますので,そういう気持ちで両方求めてみましょう
という予感はプンプンしますので,そういう気持ちで両方求めてみましょう