どもども。
本日は今年の東北大入試理系数学の第4問をやっていきます~
問題はこちら

絶対値のついた関数の積分
入試問題ではよくあるパターンですね~
よくあるパターンであるがゆえに,対策はバッチリ だといいですが~
だといいですが~
何はともあれ,絶対値をはずす作業から始めなきゃです
cos(x)=cos(-x)なので,cosのほうはそもそも何も問題ではありませんね
面倒なのはsinのほうです。

積分を計算してf(x)をもっと明瞭な形で表しましょう
あとは微分して増減表・グラフを描いて値域を調べればOKですよ~
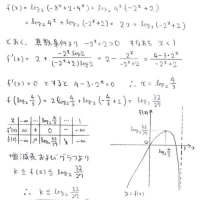
まずは0≦x≦π/2の場合からです

対数を使った積分を利用すれば簡単ですね


これで必要なデータは揃いました。
次はπ/2≦x≦πの場合です~

これを基に増減表を描きます
あとは最大値と最小値を拾い出せばおしまいデスネ


さて,対数微分を利用して積分計算しましたが,置換積分を使う手もあります
f(sin(x))cosx または f(cos(x))sinx 型の関数はそれぞれ
t=sin(x),t=cos(x) の置換で大体うまくいくのですが,
今回もそれでいけます(角の設定が若干変則的ですが)

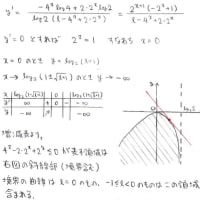
そんなこんなで求めたf(x)ですが,logの中に三角関数という形をしています。
f(x)をそのまま微分するのではなく,logの中身の関数を微分して考察する手もあります



計算自体はほんのちょっとだけ楽になったかな?て程度で大きくは変わらないですね
強いて言うなら,微分しなくても解析できる点は特徴的でしょうか

後半のほうは,微分なしだと意外と大変ですが,π/2≦x≦πの範囲では
sin(x),cos(x)は共に単調減少なのでG(x)は単調減少な関数の積になっていることが分かります

ところで,元々f(x)は定積分で与えられていましたね
次はこの積分の被積分関数に着目してみましょう

f(x)はy=g(t)のグラフとt軸と直線 t=-x と t=π/2-x で囲まれた領域の面積です



符号付き面積なので,どう考えても最小になるのは,-x=-πすなわちx=πのときですよね
最大になるのもなんとなく予想はつきます。
xがx+△xに変動したとき,f(x)の値はどれだけ変動するでしょうか

この図でいうと,S_1の分だけ増えて,S_2の分だけ減ります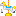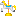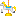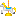
xが0に近い値のときは増える量のほうが大きくて減る量が小さいので
f(x)の値は増加しますが,増える量と減る量が一致するときを境にf(x)は
増加から減少へと転じます
では一体それはいつか。
y=g(t)のグラフがy軸対称なのでとても分かりやすいです
S_1の部分の領域とS_2の部分の領域がちょうど線対称になっているx=π/4のときですね
ただし,最小値の方はともかく,最大値の方の議論は微妙にアバウトですので
答案としてではなくあくまで参考までに,といったところでしょうか
もう1つ余談的なものをば
この問題では最初に定積分を計算してあと,出てきた関数を微分して増減を調べています。
積分して微分するんだから,出てくる導関数は元の積分の被積分関数に似たようなものになってますね
偏微分を使ってf(x)の導関数を求める話を最後に紹介します
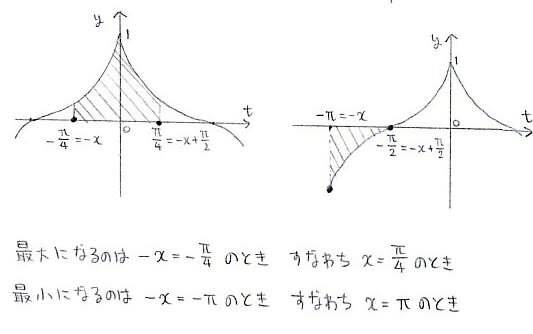
偏微分とは変数が複数ある関数を,ある特定の文字について微分する概念で
残りの変数は定数と思ってしまいます。
d/dxの代わりに∂/∂xを使います~
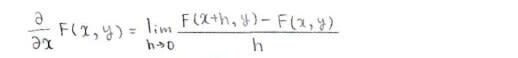
2変数関数F(x,y)にA(x),B(x)を代入した合成関数の微分,d/dx{F(A(x),B(x))}を考えます。

A,Bで偏微分した後の式には最後A,BをそれぞれA(x),B(x)に直してxの関数で表します
さて,今回の問題に適用してみます~
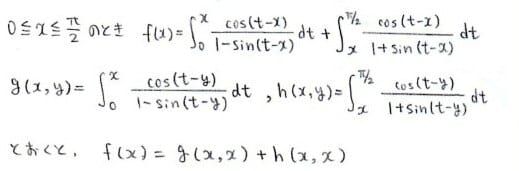
ここで,A(x)=B(x)=xとおきます

この下準備のもとで

が得られます h(x,x)についても同様です~
h(x,x)についても同様です~


そんなこんなでf(x)の導関数が得られました
後半も同様です~
前半の計算も利用できます~

なんだかんだで面倒な導出過程ではありますが,
対数や対数微分,三角関数の微分,分数関数の微分なんかは出てこずに
元の被積分関数をちゃっちゃといじってるだけであるという点は注目しておきたいところであります
本日は今年の東北大入試理系数学の第4問をやっていきます~

問題はこちら


絶対値のついた関数の積分

入試問題ではよくあるパターンですね~
よくあるパターンであるがゆえに,対策はバッチリ
 だといいですが~
だといいですが~何はともあれ,絶対値をはずす作業から始めなきゃです

cos(x)=cos(-x)なので,cosのほうはそもそも何も問題ではありませんね

面倒なのはsinのほうです。

積分を計算してf(x)をもっと明瞭な形で表しましょう

あとは微分して増減表・グラフを描いて値域を調べればOKですよ~
まずは0≦x≦π/2の場合からです


対数を使った積分を利用すれば簡単ですね



これで必要なデータは揃いました。
次はπ/2≦x≦πの場合です~


これを基に増減表を描きます

あとは最大値と最小値を拾い出せばおしまいデスネ



さて,対数微分を利用して積分計算しましたが,置換積分を使う手もあります

f(sin(x))cosx または f(cos(x))sinx 型の関数はそれぞれ
t=sin(x),t=cos(x) の置換で大体うまくいくのですが,
今回もそれでいけます(角の設定が若干変則的ですが)

そんなこんなで求めたf(x)ですが,logの中に三角関数という形をしています。
f(x)をそのまま微分するのではなく,logの中身の関数を微分して考察する手もあります




計算自体はほんのちょっとだけ楽になったかな?て程度で大きくは変わらないですね

強いて言うなら,微分しなくても解析できる点は特徴的でしょうか


後半のほうは,微分なしだと意外と大変ですが,π/2≦x≦πの範囲では
sin(x),cos(x)は共に単調減少なのでG(x)は単調減少な関数の積になっていることが分かります


ところで,元々f(x)は定積分で与えられていましたね

次はこの積分の被積分関数に着目してみましょう


f(x)はy=g(t)のグラフとt軸と直線 t=-x と t=π/2-x で囲まれた領域の面積です




符号付き面積なので,どう考えても最小になるのは,-x=-πすなわちx=πのときですよね

最大になるのもなんとなく予想はつきます。
xがx+△xに変動したとき,f(x)の値はどれだけ変動するでしょうか


この図でいうと,S_1の分だけ増えて,S_2の分だけ減ります
xが0に近い値のときは増える量のほうが大きくて減る量が小さいので
f(x)の値は増加しますが,増える量と減る量が一致するときを境にf(x)は
増加から減少へと転じます

では一体それはいつか。
y=g(t)のグラフがy軸対称なのでとても分かりやすいです

S_1の部分の領域とS_2の部分の領域がちょうど線対称になっているx=π/4のときですね


ただし,最小値の方はともかく,最大値の方の議論は微妙にアバウトですので
答案としてではなくあくまで参考までに,といったところでしょうか

もう1つ余談的なものをば

この問題では最初に定積分を計算してあと,出てきた関数を微分して増減を調べています。
積分して微分するんだから,出てくる導関数は元の積分の被積分関数に似たようなものになってますね

偏微分を使ってf(x)の導関数を求める話を最後に紹介します

偏微分とは変数が複数ある関数を,ある特定の文字について微分する概念で
残りの変数は定数と思ってしまいます。
d/dxの代わりに∂/∂xを使います~

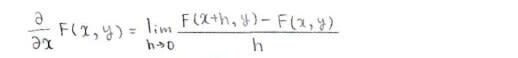
2変数関数F(x,y)にA(x),B(x)を代入した合成関数の微分,d/dx{F(A(x),B(x))}を考えます。

A,Bで偏微分した後の式には最後A,BをそれぞれA(x),B(x)に直してxの関数で表します

さて,今回の問題に適用してみます~
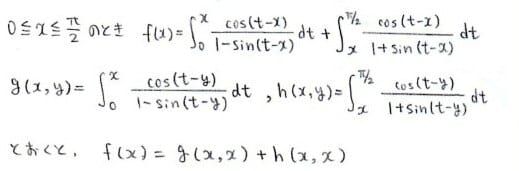
ここで,A(x)=B(x)=xとおきます


この下準備のもとで

が得られます
 h(x,x)についても同様です~
h(x,x)についても同様です~

そんなこんなでf(x)の導関数が得られました

後半も同様です~

前半の計算も利用できます~

なんだかんだで面倒な導出過程ではありますが,
対数や対数微分,三角関数の微分,分数関数の微分なんかは出てこずに
元の被積分関数をちゃっちゃといじってるだけであるという点は注目しておきたいところであります













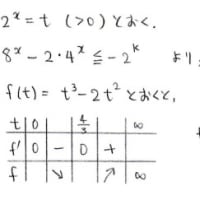


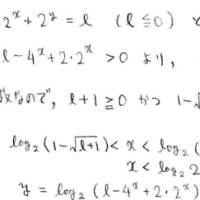

※コメント投稿者のブログIDはブログ作成者のみに通知されます