どもども。
今回は今年の京大入試理系数学の第2問をやります
問題はこちら
http://www.yozemi.ac.jp/nyushi/sokuho/recent/kyoto/zenki/sugaku_ri/mon2.html
正四面体の切断面が正三角形ならその面は底面に平行だということを確かめる問題です。
誘導などは用意されていないので自分でアプローチの仕方を探ることになります。
さてさて,△ABCも△PQRも正三角形でAP,BQ,CQが1点Oで交わるのだから,
この2つの三角形は相似の位置にあるじゃないか だから対応辺同士が平行なのは当然だ
だから対応辺同士が平行なのは当然だ
と思ったそこのアナタ その推論は本当に当たり前ですか?
その推論は本当に当たり前ですか?
後半ではそんな話にも触れてみます
とりあえず,正四面体OABCは1辺の長さを1として,
またOP=p,OQ=q,OR=rとおいておきましょう。
まずはこういう問題を解くのに便利なベクトル様を用いた解法を挙げてみます。幾何的考察はほぼせずに計算だけで終わってしまうのが魅力です


後半の(イ)は (r-q)(p-q-r)=0 と同様に得られる (p-r)(q-r-p)=0 に代入してもOKです
この手の式は対称性から,1個求めておけばあとはサイクリックに文字を置き換えるだけで
他の式が得られます。
ベクトルの代わりに余弦定理を用いても同様の解答に仕上がります

(ア)(イ)の場合分けを考察するのに幾何的アプローチを用いるのもアリです。
(ア)のときは既にQR//BCが得られています。こうなるともはや△OPQと△OPRが
正三角形になることを述べるのは容易いはず。
(イ)のときはp>q>rを仮定して構いません。そのときにPQ=QR=RPとはなり得ないことをいえばOK。


最初から幾何的考察でアタックするのもいいですね~
p>q>rと仮定して矛盾を導きましょう。
PQ=kとします。線分OQ上の点SでPS=kとなる点は多くても2個しかありません。
そのうちの1個はQです。もう一方をS'とすると,PR=k,q>rなので
OR=OS'でないといけません。そうすると上の解答の(イ)みたいな話になってきますよ


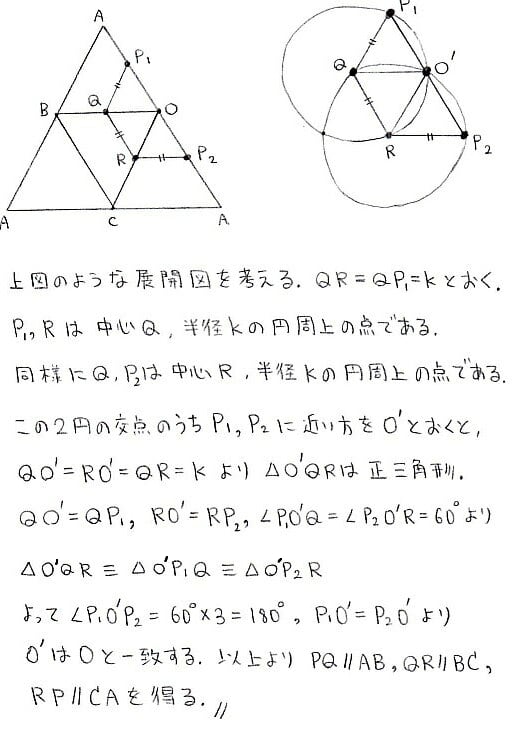
次は幾何的アプローチ第2弾で,正四面体の展開図を利用した解法です
こうなるともはや立体ではなく平面上の図形に関する問題になってしまうので
立体問題が苦手な人には向いてるかもですね~
さて,後半は冒頭に挙げた相似の位置絡みの話をしてみます。
そもそも相似の位置とはなんであったか。
2つの図形XとYがあり,Xの点とYの点の間に1対1の対応が与えられているとする。
対応する2点を結ぶ直線がすべて1点Oで交わり,Oから対応点までの距離の比が常に一定であるとき,
XとYは相似の位置にあるといい,
Oを相似の中心といいます
…ということでした
相似の位置に並べることができる,という条件で相似を定義することも多いです。
△ABCと△A'B'C'が相似の位置にあるという状況も以下の図の例のように様々あります。




今回の問題は立体版ではありますが一番最初の例のパターンにあたります。
というわけでこのパターンに着目してみます。
半直線OA,OBが作る角領域の中に△ABCと△A'B'C'がある場合です。
(1)直線AA',BB',CC'が1点Oで交わる
(2)OA:OA'=OB:OB'=OC:OC'
が与えられていれば問題なく△ABCと△A'B'C'は相似の位置にあります
しかし,今回の問題のように
(1)直線AA',BB',CC'が1点Oで交わる
(2)△ABC∽△A'B'C'
が与えられている場合は,果たして△ABCと△A'B'C'は相似の位置にあると言い切れるのでしょうか

△ABCと△A'B'C'はCA=CB,C'A'=C'B'の二等辺三角形とします。
それが上図のような配置になっているとき,見事にACとA'C'及びBCとB'C'は平行になっていません。反例です。
しかしまぁ,向きが逆になってるので点の対応関係も逆になってるとすれば,
つまりA'とB'を逆にすれば対応辺の平行関係は成り立ってますね。

それとは別に,向きも同じとして,
対応する辺同士が平行にならない場合があると仮定して考察してみましょう。
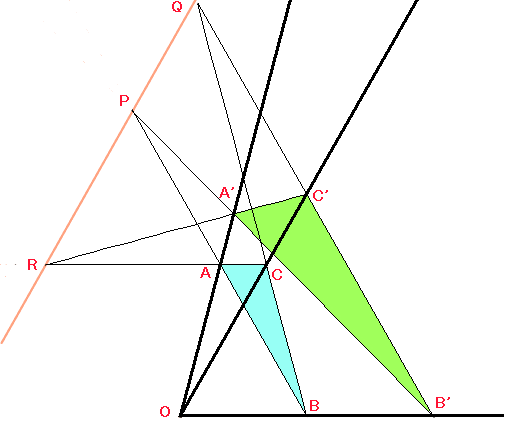
直線BAとB'A'の交点をP(∠BAA'+∠B'A'A>180°と仮定して一般性は失われません。
<180°なら図を上下ひっくり返せばいいので),BCとB'C'の交点をQ,
CAとC'A'の交点をRとおきます。
実はデザルグの定理より3点P,Q,Rは同一直線上にあるのですが,まぁそれはまた別のお話
では,△ABCと△A'B'C'の相似比を1:kとし,メネラウスの定理を使って考察してみます

かくて,
(a)4点O,A,B,Cは同一円周上にある。
(b)4点O,A',B',C'は同一円周上にある。
という必要条件が得られました。
逆にこの条件が満たされているとき,円周角の定理より
∠COB=∠CAB=∠C'A'B',∠AOC=∠ABC=∠A'B'C'
が従うので,2角相等で△ABC∽△A'B'C'となります。
従って△ABCと△A'B'C'は相似の位置にあるとは限らず,
(a)(b)の条件が満たされている状況になっていることがある,
ということが分かりました
もちろん,そのような状況はいくらでも存在します。
ちなみに上の考察において,メネラウスの定理をもっと駆使すると
△PAA'∽△QCC',△RAA'∽△QBB'もいうことができます。
下図で同じ色の印がついた角は等しくなってます

例えば△ABCと△A'B'C'が正三角形である場合を想定しましょう。
∠AOB=60°+60°=120°でない場合は
(a)(b)の条件が満たされないので,このような位置関係になるのは
△ABCと△A'B'C'が相似の位置に限るということが分かりますね
もしかしたら,(面倒なので考察してないですが
 ),
),
立体版でも似たような話が成り立って,今回の問題なんかも実は瞬時に片付けられるのかもしれないですね。
今回は今年の京大入試理系数学の第2問をやります

問題はこちら
http://www.yozemi.ac.jp/nyushi/sokuho/recent/kyoto/zenki/sugaku_ri/mon2.html
正四面体の切断面が正三角形ならその面は底面に平行だということを確かめる問題です。
誘導などは用意されていないので自分でアプローチの仕方を探ることになります。
さてさて,△ABCも△PQRも正三角形でAP,BQ,CQが1点Oで交わるのだから,
この2つの三角形は相似の位置にあるじゃないか
 だから対応辺同士が平行なのは当然だ
だから対応辺同士が平行なのは当然だ
と思ったそこのアナタ
 その推論は本当に当たり前ですか?
その推論は本当に当たり前ですか?
後半ではそんな話にも触れてみます

とりあえず,正四面体OABCは1辺の長さを1として,
またOP=p,OQ=q,OR=rとおいておきましょう。
まずはこういう問題を解くのに便利なベクトル様を用いた解法を挙げてみます。幾何的考察はほぼせずに計算だけで終わってしまうのが魅力です



後半の(イ)は (r-q)(p-q-r)=0 と同様に得られる (p-r)(q-r-p)=0 に代入してもOKです

この手の式は対称性から,1個求めておけばあとはサイクリックに文字を置き換えるだけで
他の式が得られます。
ベクトルの代わりに余弦定理を用いても同様の解答に仕上がります


(ア)(イ)の場合分けを考察するのに幾何的アプローチを用いるのもアリです。
(ア)のときは既にQR//BCが得られています。こうなるともはや△OPQと△OPRが
正三角形になることを述べるのは容易いはず。
(イ)のときはp>q>rを仮定して構いません。そのときにPQ=QR=RPとはなり得ないことをいえばOK。


最初から幾何的考察でアタックするのもいいですね~

p>q>rと仮定して矛盾を導きましょう。
PQ=kとします。線分OQ上の点SでPS=kとなる点は多くても2個しかありません。
そのうちの1個はQです。もう一方をS'とすると,PR=k,q>rなので
OR=OS'でないといけません。そうすると上の解答の(イ)みたいな話になってきますよ



次は幾何的アプローチ第2弾で,正四面体の展開図を利用した解法です

こうなるともはや立体ではなく平面上の図形に関する問題になってしまうので
立体問題が苦手な人には向いてるかもですね~


さて,後半は冒頭に挙げた相似の位置絡みの話をしてみます。
そもそも相似の位置とはなんであったか。
2つの図形XとYがあり,Xの点とYの点の間に1対1の対応が与えられているとする。
対応する2点を結ぶ直線がすべて1点Oで交わり,Oから対応点までの距離の比が常に一定であるとき,
XとYは相似の位置にあるといい,
Oを相似の中心といいます

…ということでした

相似の位置に並べることができる,という条件で相似を定義することも多いです。
△ABCと△A'B'C'が相似の位置にあるという状況も以下の図の例のように様々あります。




今回の問題は立体版ではありますが一番最初の例のパターンにあたります。
というわけでこのパターンに着目してみます。
半直線OA,OBが作る角領域の中に△ABCと△A'B'C'がある場合です。
(1)直線AA',BB',CC'が1点Oで交わる
(2)OA:OA'=OB:OB'=OC:OC'
が与えられていれば問題なく△ABCと△A'B'C'は相似の位置にあります

しかし,今回の問題のように
(1)直線AA',BB',CC'が1点Oで交わる
(2)△ABC∽△A'B'C'
が与えられている場合は,果たして△ABCと△A'B'C'は相似の位置にあると言い切れるのでしょうか


△ABCと△A'B'C'はCA=CB,C'A'=C'B'の二等辺三角形とします。
それが上図のような配置になっているとき,見事にACとA'C'及びBCとB'C'は平行になっていません。反例です。
しかしまぁ,向きが逆になってるので点の対応関係も逆になってるとすれば,
つまりA'とB'を逆にすれば対応辺の平行関係は成り立ってますね。

それとは別に,向きも同じとして,
対応する辺同士が平行にならない場合があると仮定して考察してみましょう。

直線BAとB'A'の交点をP(∠BAA'+∠B'A'A>180°と仮定して一般性は失われません。
<180°なら図を上下ひっくり返せばいいので),BCとB'C'の交点をQ,
CAとC'A'の交点をRとおきます。
実はデザルグの定理より3点P,Q,Rは同一直線上にあるのですが,まぁそれはまた別のお話
では,△ABCと△A'B'C'の相似比を1:kとし,メネラウスの定理を使って考察してみます


かくて,
(a)4点O,A,B,Cは同一円周上にある。
(b)4点O,A',B',C'は同一円周上にある。
という必要条件が得られました。
逆にこの条件が満たされているとき,円周角の定理より
∠COB=∠CAB=∠C'A'B',∠AOC=∠ABC=∠A'B'C'
が従うので,2角相等で△ABC∽△A'B'C'となります。
従って△ABCと△A'B'C'は相似の位置にあるとは限らず,
(a)(b)の条件が満たされている状況になっていることがある,
ということが分かりました

もちろん,そのような状況はいくらでも存在します。
ちなみに上の考察において,メネラウスの定理をもっと駆使すると
△PAA'∽△QCC',△RAA'∽△QBB'もいうことができます。
下図で同じ色の印がついた角は等しくなってます


例えば△ABCと△A'B'C'が正三角形である場合を想定しましょう。
∠AOB=60°+60°=120°でない場合は
(a)(b)の条件が満たされないので,このような位置関係になるのは
△ABCと△A'B'C'が相似の位置に限るということが分かりますね

もしかしたら,(面倒なので考察してないですが

 ),
),立体版でも似たような話が成り立って,今回の問題なんかも実は瞬時に片付けられるのかもしれないですね。















※コメント投稿者のブログIDはブログ作成者のみに通知されます