どもども。
今回は今年の東北大入試理系数学の第6問をやっていきますよ~
問題はこちら

漸化式が与えられた数列{a_n}が極限を持つことを示してその極限値を求める問題です~
設問は4つあって多いように見えますが,(2)なんかはほとんどサービス問題で,
また(1)(3)は同時にやってしまうことも可能です。
決して入り組んだ問題ではありません,むしろパターン問題に近いです
1.もし極限値が存在するなら,それはαでなければならない。そんなαを求める。
2.|a_n-α|≦r|a_{n-1}-α| を満たすr(0<r<1)を探す
3.0≦|a_n-α|≦r^(n-1)|a_1-α| においてハサミウチの原理
というステップを踏むことで,lim_{n→∞}a_n=α をいうことができます
とりあえず,(1)よりも先に(2)をやってしまって確実に部分点をおさえるというのがいいんじゃないでしょうか

おやおや,なんだかめんどくさそうな値なんですね,αって
では具体的に(1)(3)を考えてみたいと思います~
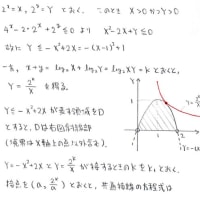
 f(x)=(3x+4)/(2x+3)の単調増加性から(1)(3)を同時に示すパターン
f(x)=(3x+4)/(2x+3)の単調増加性から(1)(3)を同時に示すパターン
漸化式に出てくるルートの中身をa_nを変数xに書き換えて,f(x)とおいてみました
ルートがついた状態の関数を考察してもいいですが,中身だけで考えたほうが楽デスネ
y=f(x)の増減を調べて(1)(3)の証明に利用しようと思います~
(1),(3)ともに数学的帰納法を用いて証明するというのが無難な作戦でしょう
それならば,手間を省かせるためにこの2つを同時に証明したいと思います。
もちろん別々にしてもOKです

反比例のグラフを平行移動しただけなので,わざわざ微分などする必要はないです
このグラフから,x>0においてf(x)が単調増加な関数であることが分かります~
さて,(1)(3)を数学的帰納法で示すということはつまり,どういうことでしょう
n=1のとき a_1<α
n≧2のとき 1<a_n<α
を示すってことですね

 a_{n+1}=√(1+g(a_n))の形にして(1)を示すパターン
a_{n+1}=√(1+g(a_n))の形にして(1)を示すパターン
(1)はa_n>1を示す問題です。ということは
a_{n+1}=√(1+g(a_n))の形に直したとき,g(a_n)>0になってることを確認することで証明する方法が考えられますね

 α^2と(a_n)^2の大小を比較して(3)を示すパターン
α^2と(a_n)^2の大小を比較して(3)を示すパターン
(1)によってa_n>0であることは分かりましたので,a_n<αを証明するためには
(a_n)^2<α^2を示せば十分であることがわかります


 数列{a_n}が単調増加列であることを利用して(1)(3)を示すパターン
数列{a_n}が単調増加列であることを利用して(1)(3)を示すパターン
今回の問題の数列{a_n}は実は単調増加列になっています。そのことが何か利用できそうです
y=√f(x)のグラフと直線y=xのx>0における交点は(α,α)になっています。
1≦x<αのとき,x<√f(x)となっていることに注意すると,
x=a_n(n≧1)のとき a_n<√f(a_n)=a_{n+1} となっています
従って,1=a_1<a_2<a_3<…<a_nが得られます~
また1≦x<αのときは, √f(x)<√f(α)=α が成り立つので
a_n<αも得られてしまいます


今回に限らず,漸化式 a_{n+1}=f(a_n) の形で与えられた数列の考察に
y=f(x)のグラフを用いるという発想はしばしば有効です
グラフを用いずに,計算で単調増加性を示すパターンも考えてみます

それを利用して(3)をやってみます~


 ハサミウチで(4)をやっつける
ハサミウチで(4)をやっつける
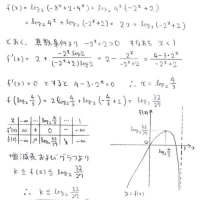
最後に(4)をやっつけましょう
冒頭で述べたように,やることはパターン化されているので,rを見つけさえすればあとは楽勝です
rの見つけ方は幾つかやり方があるでしょうね
(3)までで使った計算結果なんかを利用するといいですよ
f(α)-f(a_{n})型の式は大体式を整理するとα-a_nが出てくるので(因数定理みたいなもん),約分に役立ちます

rの取り方も上の解答のように1/50にこだわる必要もなく,1/25とか1/5なんかでも構いません
別の取りかたを考えてみます


もういっちょ


 上に有界な単調増加列が極限を持つことを利用するパターン
上に有界な単調増加列が極限を持つことを利用するパターン
これはちょっと参考までにって感じですが~~
上にあった図とか見ても分かるように,数列{a_n}は単調に増加しながらαに近づいていくという動き方をします。
一般に数列{a_n}が上に有界であるとは,nに依存しない定数M>0が何か存在して,
任意のnに対してa_n<Mが成り立っていることを言います
今回の場合はM=αにすることが可能ですね。M=100とかM=10000とかでもいいですね
とりあえず取りうる値に天井があるって言うことです~
さて,上に有界な数列{a_n}がもしも単調増加列だったとしたら…
{a_n}は振動することもなくひたすら値が大きくなり続けるわけで,それでいて取り得る値に天井があるということは
すなわち数列{a_n}は極限を持つという結論に至ります
このことは実数論における公理みたいなもんで,幾つか同値な命題があります
大学数学で最初に学ぶような話になってます
長くなってきたので深入りはしないことにして,今回の問題の数列がまさに上に有界な単調増加列なので,
rなんて定数を用いずともズバッと極限の存在性は言えてしまう訳であります

今回は今年の東北大入試理系数学の第6問をやっていきますよ~

問題はこちら


漸化式が与えられた数列{a_n}が極限を持つことを示してその極限値を求める問題です~

設問は4つあって多いように見えますが,(2)なんかはほとんどサービス問題で,
また(1)(3)は同時にやってしまうことも可能です。
決して入り組んだ問題ではありません,むしろパターン問題に近いです

1.もし極限値が存在するなら,それはαでなければならない。そんなαを求める。
2.|a_n-α|≦r|a_{n-1}-α| を満たすr(0<r<1)を探す
3.0≦|a_n-α|≦r^(n-1)|a_1-α| においてハサミウチの原理
というステップを踏むことで,lim_{n→∞}a_n=α をいうことができます

とりあえず,(1)よりも先に(2)をやってしまって確実に部分点をおさえるというのがいいんじゃないでしょうか


おやおや,なんだかめんどくさそうな値なんですね,αって

では具体的に(1)(3)を考えてみたいと思います~

 f(x)=(3x+4)/(2x+3)の単調増加性から(1)(3)を同時に示すパターン
f(x)=(3x+4)/(2x+3)の単調増加性から(1)(3)を同時に示すパターン漸化式に出てくるルートの中身をa_nを変数xに書き換えて,f(x)とおいてみました

ルートがついた状態の関数を考察してもいいですが,中身だけで考えたほうが楽デスネ

y=f(x)の増減を調べて(1)(3)の証明に利用しようと思います~
(1),(3)ともに数学的帰納法を用いて証明するというのが無難な作戦でしょう

それならば,手間を省かせるためにこの2つを同時に証明したいと思います。
もちろん別々にしてもOKです


反比例のグラフを平行移動しただけなので,わざわざ微分などする必要はないです

このグラフから,x>0においてf(x)が単調増加な関数であることが分かります~
さて,(1)(3)を数学的帰納法で示すということはつまり,どういうことでしょう
n=1のとき a_1<α
n≧2のとき 1<a_n<α
を示すってことですね


 a_{n+1}=√(1+g(a_n))の形にして(1)を示すパターン
a_{n+1}=√(1+g(a_n))の形にして(1)を示すパターン(1)はa_n>1を示す問題です。ということは
a_{n+1}=√(1+g(a_n))の形に直したとき,g(a_n)>0になってることを確認することで証明する方法が考えられますね


 α^2と(a_n)^2の大小を比較して(3)を示すパターン
α^2と(a_n)^2の大小を比較して(3)を示すパターン(1)によってa_n>0であることは分かりましたので,a_n<αを証明するためには
(a_n)^2<α^2を示せば十分であることがわかります



 数列{a_n}が単調増加列であることを利用して(1)(3)を示すパターン
数列{a_n}が単調増加列であることを利用して(1)(3)を示すパターン今回の問題の数列{a_n}は実は単調増加列になっています。そのことが何か利用できそうです

y=√f(x)のグラフと直線y=xのx>0における交点は(α,α)になっています。
1≦x<αのとき,x<√f(x)となっていることに注意すると,
x=a_n(n≧1)のとき a_n<√f(a_n)=a_{n+1} となっています

従って,1=a_1<a_2<a_3<…<a_nが得られます~
また1≦x<αのときは, √f(x)<√f(α)=α が成り立つので
a_n<αも得られてしまいます



今回に限らず,漸化式 a_{n+1}=f(a_n) の形で与えられた数列の考察に
y=f(x)のグラフを用いるという発想はしばしば有効です

グラフを用いずに,計算で単調増加性を示すパターンも考えてみます


それを利用して(3)をやってみます~



 ハサミウチで(4)をやっつける
ハサミウチで(4)をやっつける最後に(4)をやっつけましょう

冒頭で述べたように,やることはパターン化されているので,rを見つけさえすればあとは楽勝です

rの見つけ方は幾つかやり方があるでしょうね

(3)までで使った計算結果なんかを利用するといいですよ

f(α)-f(a_{n})型の式は大体式を整理するとα-a_nが出てくるので(因数定理みたいなもん),約分に役立ちます


rの取り方も上の解答のように1/50にこだわる必要もなく,1/25とか1/5なんかでも構いません

別の取りかたを考えてみます


もういっちょ



 上に有界な単調増加列が極限を持つことを利用するパターン
上に有界な単調増加列が極限を持つことを利用するパターンこれはちょっと参考までにって感じですが~~

上にあった図とか見ても分かるように,数列{a_n}は単調に増加しながらαに近づいていくという動き方をします。
一般に数列{a_n}が上に有界であるとは,nに依存しない定数M>0が何か存在して,
任意のnに対してa_n<Mが成り立っていることを言います

今回の場合はM=αにすることが可能ですね。M=100とかM=10000とかでもいいですね

とりあえず取りうる値に天井があるって言うことです~
さて,上に有界な数列{a_n}がもしも単調増加列だったとしたら…
{a_n}は振動することもなくひたすら値が大きくなり続けるわけで,それでいて取り得る値に天井があるということは
すなわち数列{a_n}は極限を持つという結論に至ります

このことは実数論における公理みたいなもんで,幾つか同値な命題があります

大学数学で最初に学ぶような話になってます

長くなってきたので深入りはしないことにして,今回の問題の数列がまさに上に有界な単調増加列なので,
rなんて定数を用いずともズバッと極限の存在性は言えてしまう訳であります

















※コメント投稿者のブログIDはブログ作成者のみに通知されます