どもども。
前回に引き続いて今年の京大入試理系数学第6問を取り扱っていきます
問題:http://www.yozemi.ac.jp/nyushi/sokuho/recent/kyoto/zenki/sugaku_ri/mon6.html
前回:http://blog.goo.ne.jp/mathnegi/e/5db101a423ac4dfec98e19f118e41750
これの別解と,関連する注意事項について今回は述べてみます
ではまず,前回と同様に確率q_kを定義しておきましょう~

ここで,前回の二つ目の解法を再掲してみます


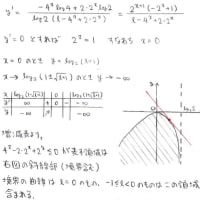
これと似た解法を挙げます

(-√3+1)≦-1/Y_{k-1}≦(-√3+1)/2 と, (√3+1)/2≦Y_{k}≦(√3+1)
を辺々足すことで(-√3+3)≦X_{k}≦(√3+3)/2 というX_kの取り得る範囲を出しています。
残りの場合も同様です


先に挙げた解法と今挙げた解法の違いを考えてみます
先に挙げた方は,1/Y_{k-1}の値に応じて条件を満たせるX_kが変わってくるので,
X_k=1のみ,X_k=1または2,X_k=2のみ,
のそれぞれの場合になる1/Y_{k-1}の範囲を求めてそれで場合分けした,というものです
一方後者は,p_k,q_k,r_kの定義式に出てくる不等式を参考にして
1/Y_{k-1}について,とりあえず無難な範囲で場合分けして考察してみました~ というものです。
というものです。
つまりこのように条件分岐させた必然性は無くて,
"根拠のある場合分け"ではなくて"期待を込めた場合分け"であるわけです。
X_kに関する不等式からX_kの候補値をあぶり出して(これが必要性),
それが実際に条件を満たすことをチェックする(これが十分性),
という作業をしていることが目に付きます。
テキトーに根拠の無い場合分けをしたのでこういった作業をしなければなりません
もし,この作業を怠ったらどうなるか,別の場合分けをした答案を考えてみます。

これは最初の場合分けと2番目の場合分けを合併しているものです。
このときは,実際は対応するX_kが,X_k=1のみ,の場合と,X_k=1または2,の場合が
混在しているわけですから,上の答案は常に"X_k=1または2"としているため誤りです

こういうことが起こり得るので,要注意 というわけなのです。
というわけなのです。
もし,この場合分けで考えるなら,どういう風にすればいいんでしょう。
それは,(√3-1)/2≦1/Y_{k-1}≦(√3-1) という大きな場合分けの中で
更にそれを細かく分類すればいいんです


もうひとつ,似たような答案を挙げてみます

X_kの不等式がさっきとは違っています。
これは,α≦X_k≦β と (√3-1)/2≦1/Y_{k-1}≦(√3-1) を辺々足して
出てくる不等式がp_kの定義に対応する (√3+1)/2≦Y_{k}≦(√3+1) になるように
αとβを求めた,という事にあたりますね
それで出てきたのが1≦X_k≦2である,と。
さっき出てきたのは(-√3+3)/2≦X_{k}≦(√3+3)/2 でした。
同じ不等式たちをいじいじしてたはずなのに,何で違う不等式が出てきたんでしょうねぇ
(√3+1)/2≦Y_k≦(√3+1) という条件を満たすX_kの範囲はY_{k-1}の値ごとに変わってきます。
具体的には1/Y_{k-1}=aとおくと, (√3+1)/2-a≦X_k≦(√3+1)-a です。
これを (√3-1)/2≦1/Y_{k-1}≦(√3-1) であるようなY_{k-1}全ての分について
合併したのが(-√3+3)/2≦X_k≦(√3+3)/2 です
言い換えると,これを満たすどのX_kに対しても必ず最低1個は(√3+1)/2≦Y_k≦(√3+1) を満たすようなY_{k-1}が存在しますよ~~っていうわけです
だから,ここから出てくるX_k=1,2は,この時点では, (√3-1)/2≦1/Y_{k-1}≦(√3-1) を満たす
全てのY_{k-1}に対して (√3+1)/2≦Y_k≦(√3+1) を満たす保証はありません(だから十分性のチェックが要ります)。
とりあえず必要条件にはなるので,全てのY_{k-1}に対して (√3+1)/2≦Y_k≦(√3+1) を満たすような
X_kがあるとするならばそれはX_k=1または2以外にはあり得んというわけですな
一方で, (√3+1)/2-a≦X_k≦(√3+1)-a に関して,
(√3-1)/2≦1/Y_{k-1}≦(√3-1) であるようなY_{k-1}全ての分の
共通部分をとったものが1≦X_k≦2です。
言い換えると, (√3-1)/2≦1/Y_{k-1}≦(√3-1) を満たすどのY_{k-1}に対しても
必ず(√3+1)/2≦Y_k≦(√3+1) を満たすようなX_kの範囲が1≦X_k≦2ですよ~~っていうわけです
だから,X_k=1または2のときは, (√3-1)/2≦1/Y_{k-1}≦(√3-1) を満たす全てのY_{k-1}に対して
(√3+1)/2≦Y_k≦(√3+1) を満たすよ♪てことは分かるものの,それとは別に
一部のY_{k-1}の値に関しては(√3+1)/2≦Y_k≦(√3+1) を満たすような別のX_kが
存在する可能性が否定できません
具体例を見てみましょ

(√3-1)/2≦1/Y_{k-1}≦(√3-1) のときはX_k=2も条件を満たすのに省かれてしまっています。
このようなことが起こり得るので要注意 てわけですね
てわけですね
よって,一見正しそうに見える以下の答案は減点対象になります。




こーいうのは,急いでると採点する側も見落としてしまいそうになっちゃうパターンですね
自分がやってる操作の必要性,十分性には常に注意を払いたいものであります
次回もまだこの問題を取り扱います~
連分数を題材にした問題なので,そういう観点に着目してこの問題を解いてみたいと思いますです
前回に引き続いて今年の京大入試理系数学第6問を取り扱っていきます

問題:http://www.yozemi.ac.jp/nyushi/sokuho/recent/kyoto/zenki/sugaku_ri/mon6.html
前回:http://blog.goo.ne.jp/mathnegi/e/5db101a423ac4dfec98e19f118e41750
これの別解と,関連する注意事項について今回は述べてみます

ではまず,前回と同様に確率q_kを定義しておきましょう~


ここで,前回の二つ目の解法を再掲してみます



これと似た解法を挙げます


(-√3+1)≦-1/Y_{k-1}≦(-√3+1)/2 と, (√3+1)/2≦Y_{k}≦(√3+1)
を辺々足すことで(-√3+3)≦X_{k}≦(√3+3)/2 というX_kの取り得る範囲を出しています。
残りの場合も同様です



先に挙げた解法と今挙げた解法の違いを考えてみます

先に挙げた方は,1/Y_{k-1}の値に応じて条件を満たせるX_kが変わってくるので,
X_k=1のみ,X_k=1または2,X_k=2のみ,
のそれぞれの場合になる1/Y_{k-1}の範囲を求めてそれで場合分けした,というものです

一方後者は,p_k,q_k,r_kの定義式に出てくる不等式を参考にして
1/Y_{k-1}について,とりあえず無難な範囲で場合分けして考察してみました~
 というものです。
というものです。つまりこのように条件分岐させた必然性は無くて,
"根拠のある場合分け"ではなくて"期待を込めた場合分け"であるわけです。
X_kに関する不等式からX_kの候補値をあぶり出して(これが必要性),
それが実際に条件を満たすことをチェックする(これが十分性),
という作業をしていることが目に付きます。
テキトーに根拠の無い場合分けをしたのでこういった作業をしなければなりません

もし,この作業を怠ったらどうなるか,別の場合分けをした答案を考えてみます。

これは最初の場合分けと2番目の場合分けを合併しているものです。
このときは,実際は対応するX_kが,X_k=1のみ,の場合と,X_k=1または2,の場合が
混在しているわけですから,上の答案は常に"X_k=1または2"としているため誤りです


こういうことが起こり得るので,要注意
 というわけなのです。
というわけなのです。もし,この場合分けで考えるなら,どういう風にすればいいんでしょう。
それは,(√3-1)/2≦1/Y_{k-1}≦(√3-1) という大きな場合分けの中で
更にそれを細かく分類すればいいんです



もうひとつ,似たような答案を挙げてみます


X_kの不等式がさっきとは違っています。
これは,α≦X_k≦β と (√3-1)/2≦1/Y_{k-1}≦(√3-1) を辺々足して
出てくる不等式がp_kの定義に対応する (√3+1)/2≦Y_{k}≦(√3+1) になるように
αとβを求めた,という事にあたりますね

それで出てきたのが1≦X_k≦2である,と。
さっき出てきたのは(-√3+3)/2≦X_{k}≦(√3+3)/2 でした。
同じ不等式たちをいじいじしてたはずなのに,何で違う不等式が出てきたんでしょうねぇ

(√3+1)/2≦Y_k≦(√3+1) という条件を満たすX_kの範囲はY_{k-1}の値ごとに変わってきます。
具体的には1/Y_{k-1}=aとおくと, (√3+1)/2-a≦X_k≦(√3+1)-a です。
これを (√3-1)/2≦1/Y_{k-1}≦(√3-1) であるようなY_{k-1}全ての分について
合併したのが(-√3+3)/2≦X_k≦(√3+3)/2 です

言い換えると,これを満たすどのX_kに対しても必ず最低1個は(√3+1)/2≦Y_k≦(√3+1) を満たすようなY_{k-1}が存在しますよ~~っていうわけです

だから,ここから出てくるX_k=1,2は,この時点では, (√3-1)/2≦1/Y_{k-1}≦(√3-1) を満たす
全てのY_{k-1}に対して (√3+1)/2≦Y_k≦(√3+1) を満たす保証はありません(だから十分性のチェックが要ります)。
とりあえず必要条件にはなるので,全てのY_{k-1}に対して (√3+1)/2≦Y_k≦(√3+1) を満たすような
X_kがあるとするならばそれはX_k=1または2以外にはあり得んというわけですな

一方で, (√3+1)/2-a≦X_k≦(√3+1)-a に関して,
(√3-1)/2≦1/Y_{k-1}≦(√3-1) であるようなY_{k-1}全ての分の
共通部分をとったものが1≦X_k≦2です。
言い換えると, (√3-1)/2≦1/Y_{k-1}≦(√3-1) を満たすどのY_{k-1}に対しても
必ず(√3+1)/2≦Y_k≦(√3+1) を満たすようなX_kの範囲が1≦X_k≦2ですよ~~っていうわけです

だから,X_k=1または2のときは, (√3-1)/2≦1/Y_{k-1}≦(√3-1) を満たす全てのY_{k-1}に対して
(√3+1)/2≦Y_k≦(√3+1) を満たすよ♪てことは分かるものの,それとは別に
一部のY_{k-1}の値に関しては(√3+1)/2≦Y_k≦(√3+1) を満たすような別のX_kが
存在する可能性が否定できません

具体例を見てみましょ


(√3-1)/2≦1/Y_{k-1}≦(√3-1) のときはX_k=2も条件を満たすのに省かれてしまっています。
このようなことが起こり得るので要注意
 てわけですね
てわけですね
よって,一見正しそうに見える以下の答案は減点対象になります。




こーいうのは,急いでると採点する側も見落としてしまいそうになっちゃうパターンですね

自分がやってる操作の必要性,十分性には常に注意を払いたいものであります
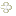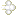
次回もまだこの問題を取り扱います~
連分数を題材にした問題なので,そういう観点に着目してこの問題を解いてみたいと思いますです













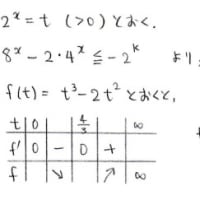


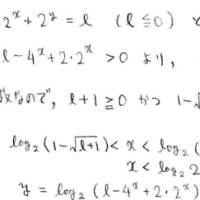

※コメント投稿者のブログIDはブログ作成者のみに通知されます