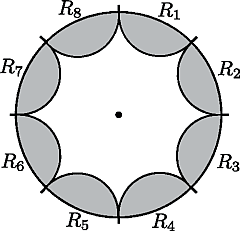
図1. 「量子重力理論は対称性を持たない」ことを背理法で証明する図。もし対称性があるとすると、それは図の灰色で塗られた部分にしか作用せず、中心の黒い点のまわりの状態には変化を起こさない。円周を細かく分けていくと、灰色の部分をいくらでも小さくできるので、対称性には、どこにも作用しないことになる。これは矛盾である。(Credit:Harlow and Ooguri)
理論物理学、基礎物理学の領域で大きなニュースが飛び込んできた。大栗博司先生(@PlankScale)とダニエル・ハーロウ先生(ホームページ)の快挙である。
量子重力には対称性はない ― 大栗機構長らが証明
https://www.ipmu.jp/ja/20190619-symmetry
発表概要:
東京大学国際高等研究所カブリ数物連携宇宙研究機構(Kavli IPMU) の大栗博司 (おおぐりひろし) 機構長は、マサチューセッツ工科大学物理学教室の Daniel Harlow 助教と共同で、重力と量子力学を統一する理論では、素粒子論の重要な原理であった対称性がすべて破れてしまうことを、ホログラフィー原理を用いて証明しました。この証明にあたっては、量子コンピューターで失われた情報を回復する鍵とされる「量子誤り訂正符号」とホログラフィー原理との間に近年発見された関係性を用いるという新たな手法が用いられました。本研究成果は、素粒子の究極の統一理論の構築に大きく貢献するものであるとともに、近年注目される量子コンピューターの発展にも寄与すると期待され、アメリカ物理学会の発行するフィジカル・レビュー・レター誌 (Physical Review Letters) に2019年5月17日付で掲載され、成果の重要性から注目論文(Editors’ Suggestion)に選ばれました。
DOI: https://doi.org/10.1103/PhysRevLett.122.191601 (2019年5月17日掲載)
論文のアブストラクト(Physical Review Letters のページ)
プレプリント (arXiv.orgのウェブページ)
2013年暮れにNHKで放送された「神の数式」で強調されていた「物理法則の対称性」が(量子物理学とアインシュタインの重力理論を統合する)量子重力理論では「ない」ことが証明されたというのだ。今後の物理学の研究への影響はとても大きい。プレプリントのほうは無料で論文を丸ごと読むことができる。
そしてこの論文では「背理法」を使って証明したそうだ。高校生に背理法の威力を教えるには格好の材料だと思う。プレプリントPDFファイルの4ページ目の「矛盾(contradiction)」と書かれている箇所が、それに該当する。

Kavli IPMUのページには「対称性に関しても、どのように破られるかを定量的に示すには至っていないことから、研究グループは今後更に研究を進めていく予定です。」と書かれている。今回の証明は「背理法」という真か偽の論理を使ったため、結果は定性的なものでしかないからだと僕は理解している。ただし今回の証明により、陽子崩壊の示唆やモノポールの存在が予測されたというのは素晴らしい。
Kavli IPMUのページにはまた、「量子コンピューターで失われた情報を回復する鍵とされる「量子誤り訂正符号」とホログラフィー原理との間に近年発見された関係性を用いるという新たな手法が用いられました。」と書かれている。プレプリントを見る限りこの手法に関する詳しい記述はなく、「量子誤り訂正符号」を使った手法はリファレンスとして記述されているダニエル・ハーロウ先生の以下の2つの論文を示すにとどめている。
[18] “The Ryu-Takayanagi formula from quantum error correction,” (2016), arXiv:1607.03901
[25] “Bulk locality and quantum error correction in AdS/CFT,” JHEP 04, 163 (2015), arXiv:1411.7041
次のページには、今回の論文やダニエル・ハーロウ先生による量子誤り訂正符号とホログラフィー原理の関連性の研究がどのようになされていたかが解説されている。
Researchers demonstrate constraints on symmetries from holography
https://phys.org/news/2019-05-constraints-symmetries-holography.html
また、経済誌「フォーブス」の電子版でとても詳しく解説されている。
Ask Ethan: What Does It Mean That Quantum Gravity Has No Symmetry?
https://www.forbes.com/sites/startswithabang/2019/06/29/ask-ethan-what-does-it-mean-that-quantum-gravity-has-no-symmetry/#6a26da033dab
掲載画像にはR1~R8という領域(R: Region)が描かれている。なぜ8までなのか僕にはよくわからないが、ホログラフィー原理におけるD8ブレインのことなのかと思ったり、もしかすると先日他界したマレー・ゲルマン博士の「八道説」なのかなと思ったりしている。
超弦理論によるハドロンの記述
http://www2.yukawa.kyoto-u.ac.jp/~kimurasho.oj/kimurasho/file/sugimoto.pdf
Hadrons in holographic QCD(D8ブレイン上の開弦理論)
http://www2.yukawa.kyoto-u.ac.jp/~masaki.murata/Masterthesis.pdf
しかし、プレプリントにはこの数が「任意(arbitrary)」だと書いてあるのと、図の説明には「円周を細かく分けていくと」と書かれているから、たまたま8個の領域を図に採用したのだと思うようになった。
また、複数の候補があがっている「超対称性理論」や「超重力理論」、「重力子」との関係はどうなるのだろうか?これらが否定されたということなのだろうか?
と書いたところ、コメント欄からhirotaさんが教えてくださった。キーポイントは今回のは「大域的対称性」が否定されたということだ。だから次のようになるという。
- 超対称性には関係ない。
- 超重力理論はとっくに否定されているから元々関係ない。(M理論に吸収されたと言った方がいいのかな?)
- 重力子は全部の基礎である場の量子論で必然だから否定されるわけもない。
発表の詳細は上記のKavli IPMUのページがいちばんわかりやすい。同じ文面をここに繰り返すのは能がない。僕にできることは論文のアブストラクトを日本語訳することくらいだ。以下に訳文を載せておく。誤訳があったらその都度直すので、ご指摘いただきたい。
発表された論文のアブストラクトの日本語訳(翻訳 by とね)
ホログラフィーによる対称性の制約
Daniel Harlow and Hirosi Ooguri
Phys. Rev. Lett. 122, 191601 - Published 17 May 2019
この論文ではAdS/CFT対応の理論における量子重力において、従来から考えられている一組の推測(が正しいこと)を示す。推測されているのは、大域的な対称性(グローバル対称性)は成り立たないこと、内部ゲージ対称性はすべての既約表現から変換される動的な対象から導かれなければならないこと、そして内部ゲージ群はコンパクトでなければならないことである。これらの推測の真実性に関して大方の見通しでは明らかではなく、AdS/CFT対応の非摂動的な一貫性から得られる結果からは自明ではない。この議論に関しての背景と詳細は、付随する論文で紹介する。
対称性については、従来から [1-3]で示される一組の推測的な制約が考えられている。(i) 量子重力は大域的な対称性を許していない。(ii) 量子重力では、いかなる内部ゲージ対称性もすべての既約表現から変換される動的な対象から導かれなければならない。(iii) 量子重力では、いかなる内部ゲージ対称性群もコンパクトでなければならない。
これらの推測のどれも古典的なラグランジアンによって正しいとは証明されていない。例えば、アインシュタインの重力に結合する自由零質量スカラー場では推測(i)と(iii)が満たされない。そしてアインシュタインの重力に結合する純粋なマックスウェル理論のゲージ不変性は推測(ii)を満たしていない。それはこれらの推測のどれもが、非摂動的な量子重力の特性に依存しているからである。これらの推測の「古典的な」議論はブラックホールの物理学に基礎を置いている。しかし、ここにはいくつもの抜け穴がある。例えば、(i)に関してこれまで議論されてこなかったことのひとつに、λφ^4 理論における φ'= -φ 対称性のような離散的大域対称性を排除するということがあげられる。そして推測の(ii)では、ある種の短距離での物理学の仮定が必要になる。(この議論の詳細は[4]を参照)
この論文のゴールはAdS/CFT対応の力を使って、少なくともこの対応の範囲内で、量子重力理論の最良の理解を得ることであり、これらの推測(が正しいこと)を確立することである。そして、その過程で理論物理学で最も基礎的な概念である大域的な対称性とゲージ対称性が本当は何を意味しているのかを明らかにすることである。この論文では[4]で紹介されている詳細を大きく省いている。また、簡潔にするために、時空座標でありふれた動きをする内部対称性のみを取り上げた。これは高い形式での対称性と同様、[4]で再び議論されている時空対称性についても言える。
リファレンス:
[1] W. Misner and J.A. Wheeler, Classical physics as geometry: Gravitation, electromagnetism, unquantized charge, and mass as properties of curved empty space, Ann. Phys. (N.Y.) 2, 525 (1957).
[2] J. Polchinski, Monopoles, duality, and string theory, Int. J. Mod. Phys. A 19, 145 (2004).
[3] T. Banks and N. Seiberg, Symmetries and strings in field theory and gravity, Phys. Rev. D 83, 084019 (2011).
[4] D. Harlow and H. Ooguri, Symmetries in Quantum Field Theory and Quantum Gravity, Symmetries in quantum field theory and quantum gravity arXiv:1810.05338
関連ページ:
大栗先生のセミナーで聞いてきた話を豆腐小僧さん(@KatagiriSo)が共有してくださった。今回の発表の背景と論文の内容に匹敵することが詳しく書かれている。
大栗さんコロキウム: ページを開く
関連動画:
この論文の内容について、大栗先生の講演と講義の動画を見つけた。最初の動画の再生開始25分あたりで紹介されている赤い本は「Holographic Quantum Matter (The MIT Press)」(Kindle版)である。
Constraints on Quantum Gravity - Hiroshi Ooguri 3/26/2018
Symmetry in Quantum Gravity by Hirosi Ooguri
Hirosi Ooguri - Constraints on Quantum Gravity 1
続き: 2 3 4
Hamilton Colloquium Series: Hiroshi Ooguri “Constraints on Quantum Gravity”
(動画を見る)
関連記事:
重力とは何か アインシュタインから超弦理論へ、宇宙の謎に迫る:大栗博司
https://blog.goo.ne.jp/ktonegaw/e/f63cdcd45ec542fa62d535b4cc715d69
強い力と弱い力:大栗博司
https://blog.goo.ne.jp/ktonegaw/e/06c3fdc3ed4e0908c75e3d7f20dd7177
大栗先生の超弦理論入門:大栗博司
https://blog.goo.ne.jp/ktonegaw/e/75dfba6307d01a5d522d174ea3e13863
「9次元からきた男」ブロガー特別試写会の感想
https://blog.goo.ne.jp/ktonegaw/e/7d229570736d1e0a174a5aca8e209f88
素粒子論のランドスケープ:大栗博司
https://blog.goo.ne.jp/ktonegaw/e/5201583450c82ac59cb4d71efe52b3d9
素粒子論のランドスケープ2:大栗博司
https://blog.goo.ne.jp/ktonegaw/e/dda75ff673f068509d46027305389ee2
Strings 2018 (6月25日~6月29日)
https://blog.goo.ne.jp/ktonegaw/e/3126bf3d2ce59f1422e00e32391d3c2c
メルマガを始めました。(目次一覧)

応援クリックをお願いします。







理論物理学、基礎物理学の領域で大きなニュースが飛び込んできた。大栗博司先生(@PlankScale)とダニエル・ハーロウ先生(ホームページ)の快挙である。
量子重力には対称性はない ― 大栗機構長らが証明
https://www.ipmu.jp/ja/20190619-symmetry
発表概要:
東京大学国際高等研究所カブリ数物連携宇宙研究機構(Kavli IPMU) の大栗博司 (おおぐりひろし) 機構長は、マサチューセッツ工科大学物理学教室の Daniel Harlow 助教と共同で、重力と量子力学を統一する理論では、素粒子論の重要な原理であった対称性がすべて破れてしまうことを、ホログラフィー原理を用いて証明しました。この証明にあたっては、量子コンピューターで失われた情報を回復する鍵とされる「量子誤り訂正符号」とホログラフィー原理との間に近年発見された関係性を用いるという新たな手法が用いられました。本研究成果は、素粒子の究極の統一理論の構築に大きく貢献するものであるとともに、近年注目される量子コンピューターの発展にも寄与すると期待され、アメリカ物理学会の発行するフィジカル・レビュー・レター誌 (Physical Review Letters) に2019年5月17日付で掲載され、成果の重要性から注目論文(Editors’ Suggestion)に選ばれました。
DOI: https://doi.org/10.1103/PhysRevLett.122.191601 (2019年5月17日掲載)
論文のアブストラクト(Physical Review Letters のページ)
プレプリント (arXiv.orgのウェブページ)
2013年暮れにNHKで放送された「神の数式」で強調されていた「物理法則の対称性」が(量子物理学とアインシュタインの重力理論を統合する)量子重力理論では「ない」ことが証明されたというのだ。今後の物理学の研究への影響はとても大きい。プレプリントのほうは無料で論文を丸ごと読むことができる。
そしてこの論文では「背理法」を使って証明したそうだ。高校生に背理法の威力を教えるには格好の材料だと思う。プレプリントPDFファイルの4ページ目の「矛盾(contradiction)」と書かれている箇所が、それに該当する。

Kavli IPMUのページには「対称性に関しても、どのように破られるかを定量的に示すには至っていないことから、研究グループは今後更に研究を進めていく予定です。」と書かれている。今回の証明は「背理法」という真か偽の論理を使ったため、結果は定性的なものでしかないからだと僕は理解している。ただし今回の証明により、陽子崩壊の示唆やモノポールの存在が予測されたというのは素晴らしい。
Kavli IPMUのページにはまた、「量子コンピューターで失われた情報を回復する鍵とされる「量子誤り訂正符号」とホログラフィー原理との間に近年発見された関係性を用いるという新たな手法が用いられました。」と書かれている。プレプリントを見る限りこの手法に関する詳しい記述はなく、「量子誤り訂正符号」を使った手法はリファレンスとして記述されているダニエル・ハーロウ先生の以下の2つの論文を示すにとどめている。
[18] “The Ryu-Takayanagi formula from quantum error correction,” (2016), arXiv:1607.03901
[25] “Bulk locality and quantum error correction in AdS/CFT,” JHEP 04, 163 (2015), arXiv:1411.7041
次のページには、今回の論文やダニエル・ハーロウ先生による量子誤り訂正符号とホログラフィー原理の関連性の研究がどのようになされていたかが解説されている。
Researchers demonstrate constraints on symmetries from holography
https://phys.org/news/2019-05-constraints-symmetries-holography.html
また、経済誌「フォーブス」の電子版でとても詳しく解説されている。
Ask Ethan: What Does It Mean That Quantum Gravity Has No Symmetry?
https://www.forbes.com/sites/startswithabang/2019/06/29/ask-ethan-what-does-it-mean-that-quantum-gravity-has-no-symmetry/#6a26da033dab
掲載画像にはR1~R8という領域(R: Region)が描かれている。なぜ8までなのか僕にはよくわからないが、ホログラフィー原理におけるD8ブレインのことなのかと思ったり、もしかすると先日他界したマレー・ゲルマン博士の「八道説」なのかなと思ったりしている。
超弦理論によるハドロンの記述
http://www2.yukawa.kyoto-u.ac.jp/~kimurasho.oj/kimurasho/file/sugimoto.pdf
Hadrons in holographic QCD(D8ブレイン上の開弦理論)
http://www2.yukawa.kyoto-u.ac.jp/~masaki.murata/Masterthesis.pdf
しかし、プレプリントにはこの数が「任意(arbitrary)」だと書いてあるのと、図の説明には「円周を細かく分けていくと」と書かれているから、たまたま8個の領域を図に採用したのだと思うようになった。
また、複数の候補があがっている「超対称性理論」や「超重力理論」、「重力子」との関係はどうなるのだろうか?これらが否定されたということなのだろうか?
と書いたところ、コメント欄からhirotaさんが教えてくださった。キーポイントは今回のは「大域的対称性」が否定されたということだ。だから次のようになるという。
- 超対称性には関係ない。
- 超重力理論はとっくに否定されているから元々関係ない。(M理論に吸収されたと言った方がいいのかな?)
- 重力子は全部の基礎である場の量子論で必然だから否定されるわけもない。
発表の詳細は上記のKavli IPMUのページがいちばんわかりやすい。同じ文面をここに繰り返すのは能がない。僕にできることは論文のアブストラクトを日本語訳することくらいだ。以下に訳文を載せておく。誤訳があったらその都度直すので、ご指摘いただきたい。
発表された論文のアブストラクトの日本語訳(翻訳 by とね)
ホログラフィーによる対称性の制約
Daniel Harlow and Hirosi Ooguri
Phys. Rev. Lett. 122, 191601 - Published 17 May 2019
この論文ではAdS/CFT対応の理論における量子重力において、従来から考えられている一組の推測(が正しいこと)を示す。推測されているのは、大域的な対称性(グローバル対称性)は成り立たないこと、内部ゲージ対称性はすべての既約表現から変換される動的な対象から導かれなければならないこと、そして内部ゲージ群はコンパクトでなければならないことである。これらの推測の真実性に関して大方の見通しでは明らかではなく、AdS/CFT対応の非摂動的な一貫性から得られる結果からは自明ではない。この議論に関しての背景と詳細は、付随する論文で紹介する。
対称性については、従来から [1-3]で示される一組の推測的な制約が考えられている。(i) 量子重力は大域的な対称性を許していない。(ii) 量子重力では、いかなる内部ゲージ対称性もすべての既約表現から変換される動的な対象から導かれなければならない。(iii) 量子重力では、いかなる内部ゲージ対称性群もコンパクトでなければならない。
これらの推測のどれも古典的なラグランジアンによって正しいとは証明されていない。例えば、アインシュタインの重力に結合する自由零質量スカラー場では推測(i)と(iii)が満たされない。そしてアインシュタインの重力に結合する純粋なマックスウェル理論のゲージ不変性は推測(ii)を満たしていない。それはこれらの推測のどれもが、非摂動的な量子重力の特性に依存しているからである。これらの推測の「古典的な」議論はブラックホールの物理学に基礎を置いている。しかし、ここにはいくつもの抜け穴がある。例えば、(i)に関してこれまで議論されてこなかったことのひとつに、λφ^4 理論における φ'= -φ 対称性のような離散的大域対称性を排除するということがあげられる。そして推測の(ii)では、ある種の短距離での物理学の仮定が必要になる。(この議論の詳細は[4]を参照)
この論文のゴールはAdS/CFT対応の力を使って、少なくともこの対応の範囲内で、量子重力理論の最良の理解を得ることであり、これらの推測(が正しいこと)を確立することである。そして、その過程で理論物理学で最も基礎的な概念である大域的な対称性とゲージ対称性が本当は何を意味しているのかを明らかにすることである。この論文では[4]で紹介されている詳細を大きく省いている。また、簡潔にするために、時空座標でありふれた動きをする内部対称性のみを取り上げた。これは高い形式での対称性と同様、[4]で再び議論されている時空対称性についても言える。
リファレンス:
[1] W. Misner and J.A. Wheeler, Classical physics as geometry: Gravitation, electromagnetism, unquantized charge, and mass as properties of curved empty space, Ann. Phys. (N.Y.) 2, 525 (1957).
[2] J. Polchinski, Monopoles, duality, and string theory, Int. J. Mod. Phys. A 19, 145 (2004).
[3] T. Banks and N. Seiberg, Symmetries and strings in field theory and gravity, Phys. Rev. D 83, 084019 (2011).
[4] D. Harlow and H. Ooguri, Symmetries in Quantum Field Theory and Quantum Gravity, Symmetries in quantum field theory and quantum gravity arXiv:1810.05338
関連ページ:
大栗先生のセミナーで聞いてきた話を豆腐小僧さん(@KatagiriSo)が共有してくださった。今回の発表の背景と論文の内容に匹敵することが詳しく書かれている。
大栗さんコロキウム: ページを開く
関連動画:
この論文の内容について、大栗先生の講演と講義の動画を見つけた。最初の動画の再生開始25分あたりで紹介されている赤い本は「Holographic Quantum Matter (The MIT Press)」(Kindle版)である。
Constraints on Quantum Gravity - Hiroshi Ooguri 3/26/2018
Symmetry in Quantum Gravity by Hirosi Ooguri
Hirosi Ooguri - Constraints on Quantum Gravity 1
続き: 2 3 4
Hamilton Colloquium Series: Hiroshi Ooguri “Constraints on Quantum Gravity”
(動画を見る)
関連記事:
重力とは何か アインシュタインから超弦理論へ、宇宙の謎に迫る:大栗博司
https://blog.goo.ne.jp/ktonegaw/e/f63cdcd45ec542fa62d535b4cc715d69
強い力と弱い力:大栗博司
https://blog.goo.ne.jp/ktonegaw/e/06c3fdc3ed4e0908c75e3d7f20dd7177
大栗先生の超弦理論入門:大栗博司
https://blog.goo.ne.jp/ktonegaw/e/75dfba6307d01a5d522d174ea3e13863
「9次元からきた男」ブロガー特別試写会の感想
https://blog.goo.ne.jp/ktonegaw/e/7d229570736d1e0a174a5aca8e209f88
素粒子論のランドスケープ:大栗博司
https://blog.goo.ne.jp/ktonegaw/e/5201583450c82ac59cb4d71efe52b3d9
素粒子論のランドスケープ2:大栗博司
https://blog.goo.ne.jp/ktonegaw/e/dda75ff673f068509d46027305389ee2
Strings 2018 (6月25日~6月29日)
https://blog.goo.ne.jp/ktonegaw/e/3126bf3d2ce59f1422e00e32391d3c2c
メルマガを始めました。(目次一覧)

応援クリックをお願いします。



























>対称性が「破れる」のではなく、「ない」のである。
>Kavli IPMUのページには「対称性に関しても、どのように破られるかを定量的に示すには至っていないことから、研究グループは今後更に研究を進めていく予定です。」と書かれている。
ないのに、破れるかを示すってどうゆうことでしょうね?
ひゃまもブログはじめて、論文アップしました、内容は丁度、非対称な
「本論は、このような古典論的相対性原理(相対論的力学)からのアプローチでなく、前期量子論に立ち返って非対称世界における量子論的相対性原理から、エネルギー密度が時間変化しない宇宙モデルの是非を議論する。」
暇があればコメントくださいw
こんにちは。今回の発表は驚きましたね。論文自体は先月公開されていたようですが、Kavli IPMUの発表は昨日になりました。
> ないのに、破れるかを示すってどうゆうことでしょうね?
そうですね。これはまだまったくわかっていないと思います。棒が倒れるような対称性の破れとは違うでしょうし。
ひゃまさんのお書きになった論文、読んでみますね。
後の方では大域的対称性の否定なんですね。
これなら超対称性には関係ないし、超重力理論はとっくに否定されているから元々関係ない。(M理論に吸収されたと言った方がいいのかな?)
そして重力子は全部の基礎である場の量子論で必然だから否定されるわけもない。
一般相対論でも大域的対称性が無くてエネルギー保存則すら導けないのに今更ですね。
と言う事で、結局は量子重力理論が難しいと言う事しか分からないなー。
はい、今回のは「大域的」対称性を否定したものです。
超対称性や超重力理論、重力子については、そのように考えればよいわけですね。教えていただき、ありがとうございました。
ひゃま的には背負うものがないので、大域的対称がない場合、それによってどのように対称性が現れるかを示したら、いいような気がします。
実際、その条件を満たすミクロな運動に限った場合にのみ、時間に対する特別な対称性が現れることが分かりました。http://www.riken.jp/pr/press/2016/20160427_2/
今後、大栗先生がどのようなアプローチで、定量的な研究をされるか興味がでてきました。
紹介いただいた理研の「乱雑さを決める時間の対称性を発見-100年前の物理と数学の融合が築くミクロとマクロの架け橋-」は実に興味深いですね。自然法則の根源にかかわることが地上で実験できてしまうところが、装置が単純に見えるところがなんとも不思議です。
そのよーな可能性は無いでしょーか?
はい、重力がゲージ場でない可能性も出てきたと思います。だとしたらどうなるの?ということは何もわかっていません。これからどのような理論が出てくるか、楽しみにしています。
そういうことになるわけですね。教えていただき、ありがとうございます。