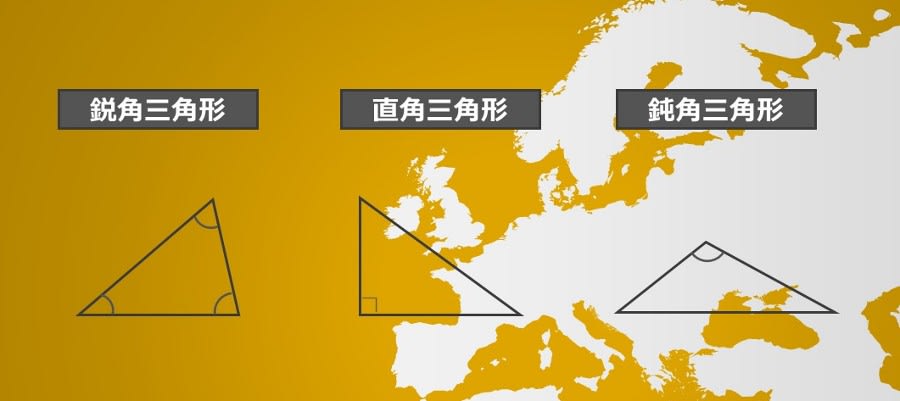
高校入試と「いろいろな三角形の定義と定理について」
数学において、
「定義」とは 「○○とは△△というもの(こと)である」 という物や事柄に与えられた意味であり、
絶対的な「決まりごと」になります。一方、
「定理」とは与えられた「決まりごと」ではなく、正しいことがすでに説明(証明)されたことがらになります。
したがって、「定理」として使用するには、はじめに正しいかどうかを説明(証明)しなければなりません。
◎ 二等辺三角形: 2辺の長さが等しい三角形(定 義)
「定 理1」: 二等辺三角形の底角は等しい
これを証明するには、 「ある三角形において、2辺が等しければ、底角は等しい」
という文章をつくります。

「定 理2」: 二等辺三角形の頂角の二等分線は底辺を垂直に2等分する
これを証明するには、 「ある三角形において、2辺が等しければ、頂角の二等分線は底辺を垂直に二等分する」
という文章を作成します。

「定 理3」: 2角が等しい三角形は二等辺三角形である
これを証明するには、 「ある三角形において、2角が等しければ、二等辺三角形になる」
という文章を作成します。

◎ 正三角形: 3辺の長さが等しい三角形(定 義)
「定 理」: 正三角形の3つの角は等しい
これを証明するには、 「ある三角形において、3辺がすべて等しければ3つの角はすべて等しい」
という文章を作成します。このとき、
3辺がすべて等しいことから、 「正三角形は二等辺三角形の特別な形」 と考え、
二等辺三角形の性質を利用します。

〈演習問題〉
「AD // BCである台形ABCDの対角線ACが∠BCDの二等分線になっているとき、
△ADCが二等辺三角形になることを証明しなさい」

〈前回の入試問題の答え〉
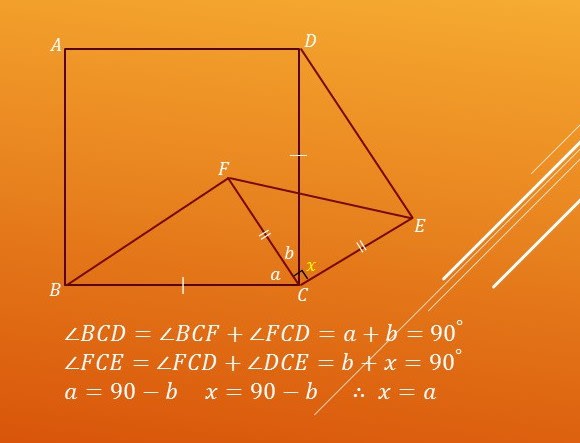
〈証 明〉
手 順1.合同対象を明らかに
△BCF と△DCE において、
手 順2. 仮定や図形の性質による説明
仮定より、 BC=DC ―― ① (正方形の1辺)
また、 CF=CE ―― ② (直角二等辺三角形の2辺)
∠BCD=∠FCE=90° であり、
∠BCD=∠BCF+∠FCD、 ∠FCE=∠FCD+∠DCE
よって、 ∠BEF=∠DCE ―― ③
手 順3.当てはまる合同条件を述べる
①~③より、
2辺の長さとその間の角がそれぞれ等しい2つの三角形は合同である
手 順4.結論づけ
→ △BCF≡△DCE である ・・・ 証明終わり

授業で学習した内容をしっかり身に着ける! ☆ [要点整理]と[演習問題]を一体化した実践学習 〉〉
☆ [要点整理]と[演習問題]を一体化した実践学習 〉〉










![受験対応[英語・数学]講座](https://blogimg.goo.ne.jp/image/upload/f_auto,q_auto,t_image_square_m/v1/user_image/5e/12/a9c129e5a32c4395c32b83e89916aa29.jpg)
![受験対応[英語・数学]講座](https://blogimg.goo.ne.jp/image/upload/f_auto,q_auto,t_image_square_m/v1/user_image/25/85/0c2e05c5f8df43a17fb40ce33cb2b0f8.jpg)
![受験対応[英語・数学]講座](https://blogimg.goo.ne.jp/image/upload/f_auto,q_auto,t_image_square_m/v1/user_image/7c/f2/14193d4d7d414be9a8950b3ef112c724.jpg)
![受験対応[英語・数学]講座](https://blogimg.goo.ne.jp/image/upload/f_auto,q_auto,t_image_square_m/v1/user_image/37/34/0476b484f16612363ad960ff05eecb95.jpg)


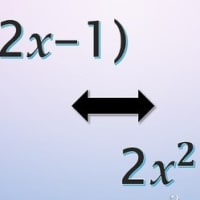

※コメント投稿者のブログIDはブログ作成者のみに通知されます