
夏休み特別講座:数学
一般公立校の高校入試、数学の問題では、第1問目に各学習項目から1問ずつ基本的な内容のもの
が出題されてきました。今年度も同様に 10 問 程度構成されています。数学は合計 5 問出題されますから、
1問当たり 6 分以内で解く必要があります。1問目のような基本問題は、日頃からいくつもこなして、
どのようなものでも確実に解答できるようにしておきましょう。
1. 次の各問いに答えなさい。
(1) 次の計算をしなさい。
ア -12 + 3 ÷ 6
イ 3/5 - 8/7
* 四則計算のルールを思い出します
ウ 48a2b2 ÷ 3ab2
* 累乗計算のルール ambn = a m+n, (a m)n = a m×n
を利用
エ 8√3 + √108
* √a2b = a√b を利用
(2) (x+2)2 - (x+3)(x-5) を計算しなさい。
* 展開して式を整理します
(3) (x+1)2 - 2(x+1) - 24 を因数分解しなさい。
* x+1 = A に置きかえて「たすきがけの因数分解」を行います
(4) 2次方程式 4x2 - 9x + 3 = 0 を解きなさい。
* まず、平方公式が使えるかを確認し、使えなければ「解の公式」を利用
(5) √1440n が自然数となるような、最も小さい自然数 n の値を求めなさい。
* 1440 を素因数分解して、ある数の 2 乗の形にならない素数を見つけます
(6) 関数 y=-1/4x2 について、x の変域が - 6 ≦ x ≦ 4 のとき、y の変域は
a ≦ y ≦ b である。このとき、a, b の値を求めなさい。
* 関数に -6, 4 を代入します
(7) 連続する 2 つの自然数があり、それぞれを 2 乗した数の和が 117 になるとき、
小さい方の自然数を答えなさい。
* 1 ~ 9 までの自然数を 2 乗し、それら 2 数の和のうち、一の位が 7 のものを見つけます
(8) 次の資料は、ある農園で収穫したトマト 20 個のそれぞれの重さ(単位 g)の記録である。
このとき、この資料におけるメジアンを求めなさい。
「142 157 107 188 115 146 173 123 106 139
162 114 135 151 192 174 166 143 135 122」
* 資料を小さい順に並べ替えます
(9) 図のような平行四辺形 ABCD があり、辺 BC の中点を E とする。また、辺 AB 上に
点 F を AF : FB = 4 : 3 となるようにとり、辺 DC 上に点 G を AD // FG となる
ようにとる。線分 AE と線分 FG との交点を H, DE と線分 FG との交点を I とする。
このとき、三角形 AFH と三角形 EHI の面積比を最も簡単な整数の比で表しなさい。
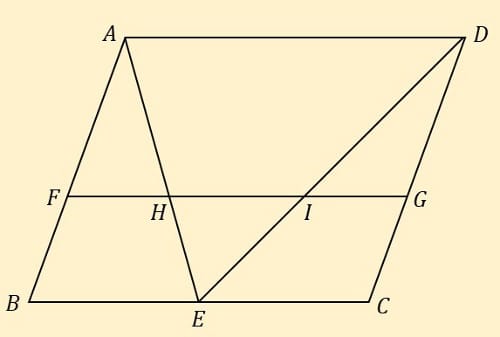
* 平行線と線分の比を利用、各比の値を長さに見立てます

— 答 え —
(1) ア = -12+1/2 = -23/2
イ = 21/35 - 40/35 = -19/35
ウ = 48/3 × a2-1 × b2 - 2 = 16 × a × 1 = 16a
エ = 8√3 + √2×2×3×3×3 = 8√3 + 6√3 = 14√3
(2) = x2+4x+4 - (x2 - 2x - 15) = x2 - x2+4x+2x+15 = 6x+15
(3) A2 - 2A - 24 = (A+4)(A - 6) = (x+1+4)(x+1-6) = (x+5)(x - 5)
(4)
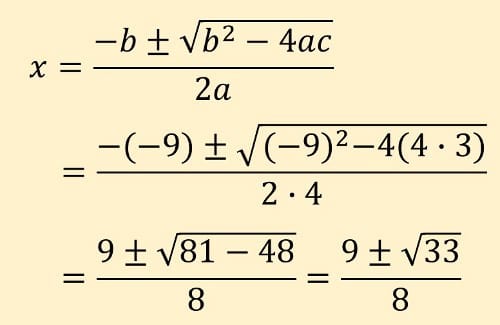
(5) 1440 = 2×720 = 2×2×360 = 2×2×2×180 = 2×2×2×2×90
= 2×2×2×2×2×45 = 2×2×2×2×2×3×15
= 2×2×2×2×2×3×3×5= 25×32×5
25×32×5×2×5 = 26×32×52 = (8×3×5)2 = 1202 = 14400
∴ n = 10
(6) y = -1/4x2 において、
x = -6 のとき y = -1/4×(-6)2 = -1/4×36 = -9
x = 4 のとき y = -1/4×(4)2 = -1/4×16 = -4
よって、
x の変域が - 6 ≦ x ≦ 4 のとき、y の変域は -9 ≦ y ≦ -4
∴ a = -9, b = -4
(7) 1 ~ 9 までの自然数を 2 乗は、 1, 4, 9, 16, 25, 36, 49, 64, 81
これらのうち、一の位が 7 のものは、36+81 = 117
よって、6 と 9 の2乗の和になります
∴ 6
(8) 資料を小さい順に並べると、
106 107 114 115 122 123 135 135 139 142
143 146 151 157 162 166 173 174 188 192
偶数個の資料の中央値は真ん中の 2 数 の平均なので、
(142 + 143) ÷ 2 = 142.5
∴ 142.5 g
(9) △AFH = 2×3 ÷ 2=3, △EHI = 3×3 ÷ 2=9/2
△AFH : △EHI = 3 : 9/2 = 6 : 9 = 2 : 3
∴ 2 : 3









