@http://blog.goo.ne.jp/bonsai-chat/e/58a7d944c688bfbe530afac1e955ae7f
=G7B%1:中1の数学
/現行学習指導要領からの引用です.
%1: 目標
- (1) 数を正の数と負の数まで拡張し,数の概念についての理解を深める。また,文字を用いることや方程式の必要性と意味を理解するとともに,数量の関係や法則などを一般的にかつ簡潔に表現して処理したり,一元一次方程式を用いたりする能力を培う。
- (2) 平面図形や空間図形についての観察,操作や実験などの活動を通して,図形に対する直観的な見方や考え方を深めるとともに,論理的に考察し表現する能力を培う。
- (3) 具体的な事象を調べることを通して,比例,反比例についての理解を深めるとともに,関数関係を見いだし表現し考察する能力を培う。
- (4) 目的に応じて資料を収集して整理し,その資料の傾向を読み取る能力を培う。
%2:2 内容
%21A: 数と式
- %21A1:(1)具体的な場面を通して正の数と負の数について理解し,その四則計算ができるようにするとともに,正の数と負の数を用いて表現し考察することができるようにする。
- ア 正の数と負の数の必要性と意味を理解すること。
- イ 小学校で学習した数の四則計算と関連付けて,正の数と負の数の四則計算の意味を理解すること。
- ウ 正の数と負の数の四則計算をすること。
- エ 具体的な場面で正の数と負の数を用いて表したり処理したりすること。
%21A11:負の数の計算
[?G7B:負の数の掛け算],[?G6E:「0」の扱い]参照.
- %21A2:(2)文字を用いて数量の関係や法則などを式に表現したり式の意味を読み取ったりする能力を培うとともに,文字を用いた式の計算ができるようにする。
- ア 文字を用いることの必要性と意味を理解すること。
- イ 文字を用いた式における乗法と除法の表し方を知ること。
- ウ 簡単な一次式の加法と減法の計算をすること。
- エ 数量の関係や法則などを文字を用いた式に表すことができることを理解し,式を用いて表したり読み取ったりすること。
%21A21:乗法と除法の式表現
[?G5R:分数の計算]の([%2]:掛け算と割り算)参照.
・「÷」は使いません.
- %21A3:(3)方程式について理解し,一元一次方程式を用いて考察することができるようにする。
- ア 方程式の必要性と意味及び方程式の中の文字や解の意味を理解すること。
- イ 等式の性質を基にして,方程式が解けることを知ること。
- ウ 簡単な一元一次方程式を解くこと及びそれを具体的な場面で活用すること。
%21A31:一元一次方程式
[1]【中学数学】1次方程式(xの方程式)の解き方の3つの手順?基礎編 ...
http://media.qikeru.me/x-equation/
・分り易く説明されています.
[2]一元一次方程式と連立方程式の共通点と相違点を教えてください ...
http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1265325452
[3]一次方程式の解き方 : 方程式・関数ほか数学の問題の解き方
http://blog.livedoor.jp/suugaku_tokikata/archives/51429064.html
- %21A:〔用語・記号〕
- 自然数 符号 絶対値 項 係数 移項
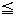
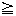
- 自然数 符号 絶対値 項 係数 移項
%21B:B 図形
- %21B1:(1)観察,操作や実験などの活動を通して,見通しをもって作図したり図形の関係について調べたりして平面図形についての理解を深めるとともに,論理的に考察し表現する能力を培う。
- ア 角の二等分線,線分の垂直二等分線,垂線などの基本的な作図の方法を理解し,それを具体的な場面で活用すること。
- イ 平行移動,対称移動及び回転移動について理解し,二つの図形の関係について調べること。
%21B11:[GCH:小学校で学ぶ図形] 参照.
%21B111:定規とコンパスによる作図
/[1]二等分線 - Wikipedia
http://ja.wikipedia.org/wiki/%E4%BA%8C%E7%AD%89%E5%88%86%E7%B7%9A
[2]作図の3種類(垂直二等分線、角の二等分線、垂線)は ... - アメーバブログ
http://ameblo.jp/pipinee/entry-12224656402.html
- %21B2:(2) 観察,操作や実験などの活動を通して,空間図形についての理解を深めるとともに,図形の計量についての能力を伸ばす。
- ア 空間における直線や平面の位置関係を知ること。
- イ 空間図形を直線や平面図形の運動によって構成されるものととらえたり,空間図形を平面上に表現して平面上の表現から空間図形の性質を読み取ったりすること。
- ウ 扇形の弧の長さと面積並びに基本的な柱体,錐(すい)体及び球の表面積と体積を求めること。
%21B:〔用語・記号〕 -
- 弧 弦 回転体 ねじれの位置 π ∥ ⊥ ∠ Δ
%21B21:[?GCR:面積と体積の計算]参照.
%21B22:空間図形
[1]立体を分類して,その成り立ちを探ろう
http://shinko-keirin.co.jp/keirinkan/j-kadaimath/0807_2/index.htm
[2]中学1年生 数学 【空間図形】立体の表し方 練習プリント 無料ダウンロード
http://happylilac.net/jhs-math1_06-02.html
- 弧 弦 回転体 ねじれの位置 π ∥ ⊥ ∠ Δ
%21C:C関数
- %21C1:(1)具体的な事象の中から二つの数量を取り出し,それらの変化や対応を調べることを通して,比例,反比例の関係についての理解を深めるとともに,関数関係を見いだし表現し考察する能力を培う。
- ア 関数関係の意味を理解すること。
- イ 比例,反比例の意味を理解すること。
- ウ 座標の意味を理解すること。
- エ 比例,反比例を表,式,グラフなどで表し,それらの特徴を理解すること。
- オ 比例,反比例を用いて具体的な事象をとらえ説明すること。
%21C11:比例,反比例
[1][?GCT:小学校で学ぶ測定と数量関係 ]の([%G7A%6].[%21D21])
[2]「比例のグラフ」が、すぐにかけるコツ! | 中1生の「数学」アップ法
http://www.all5.jp/subject/114.html
%21C12:関数
%21C121:参考資料
[1]関数とは何か、の中学生への噛み砕いた説明の仕方を教えて下さい ...
http://oshiete.goo.ne.jp/qa/5940727.html
[2]中1 関数 - 数学 解決済 | 教えて!goo
http://oshiete.goo.ne.jp/qa/8885913.html
[1]【中学数学】関数とは何ものなのか???
http://media.qikeru.me/function-is/
[3]中1 4章 変化と関数① ~関数とは?
http://naokorone.hatenablog.com/entry/2015/11/01/190608
[4]関数(中1)
http://www.tcp-ip.or.jp/~endou/sisaku2/22.htm
[5]合成関数と逆関数を馬鹿でもわかるくらいわかりやすく
http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1116364326
[6]逆関数とは何か - 数学 締切済 | 教えて!goo
http://oshiete.goo.ne.jp/qa/4915132.html
[7]逆関数の3つの定義と使い分け | 高校数学の美しい物語
http://mathtrain.jp/inverse
[8]逆関数
http://www.sist.ac.jp/~kanakubo/research/hosoku/gyakukansuu.html
[9]逆関数
http://www.geisya.or.jp/~mwm48961/kou3/inverse_fun1.htm
[10]逆関数の意味|数学|苦手解決Q&A|進研ゼミプラス高校講座 ...
http://kou.benesse.co.jp/nigate/math/a14m2102.html
[11]数学で出てくる用語「変域」とは具体的に何を表...
http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1421924619
[12]【中学数学】関数の「変域」ってなんだろう??
http://media.qikeru.me/heniki/
[13]変域
http://www.geisya.or.jp/~mwm48961/math2/m3range1.htm
・関数 y=x2 において,xの変域が -1≦x≦2のとき,yの変域を求めなさい
%21C122:関数の使用例
[?GCR:面積と体積の計算]の([%11]:鋭角三角形「△ABC」)で関数の例を説明する.直角三角形「△ABH」の底辺の長さ『BH』を「3」cm,高さ『AH』を「4」cmとすると,面積『△ABH』は「6」cm2である.
%21C1221:関数の記号
「△ABH」を「x」倍に拡大した直角三角形の底辺の長さを
「f1(x)」cm,高さを「f2(x)」cm,面積を「f3(x)」cm2で表わすと,「f1(x)=3x」,「f2(x)=4x」,「f3(x)=6x」
・e.g.「f1(10)=30」,「f2(10)=40」,「f3(10)=60」
・「y1=f1(x)」,「y2=f2(x)」,「y3=f3(x)」とすると
「y2=(4/3)y1」(比例),「y3/y1=2y1」(反比例)
・cf.高校の物理では物理量を単位付きの数値で扱う(e.g.「100[V]×5[A]×6[h]=3[kWh]」).
%21C1222:変数
「f(□1)=□2」のとき「□1」を「独立変数」,「□2」を「従属変数」という(「□1」を変化させたとき,これに応じて「□2」が変わる).
・「□1」を変化させたときの「□2」が変化する範囲を考えさせたいようです.
・[%21C121]:参考資料[11]の疑問は当然.範囲全般に「変域」を使うようです(e.g.[12],[13]). - ・通常の授業では「y=3x」と書けば(「x」が独立変数,「y」が従属変数で)「x」の「変域」が「1≦x≦2」のとき「y」の「変域」は「3≦y≦6」であると教えている?
・大学生は「f1:A→A」,「f1(x)=3x」」のようにかく(「A」は正の実数の集合).「f1」の定義域は「A」,値域は「f1(A)」.
・「□1∈B「B⊂A」」とすると「□2∈f1(B)」.
[G6M%1:集合と写像](大学生用)の([%15]:写像)参照.
%21C223:逆関数
「y=f(x)」である「x」が関数「g」を用いて「x=g(y)」と表現できるとき「g」を「f」の逆関数(逆写像)といい,「f-1」で表わす.
・「f-1(x)(x)≠1/f-1(x)」に注意.(e.g.「y=f(x)」,「f(x)=3x」ならば「y=3x」,「x=y/3」だから「f-1(y)=y/3」.
%21C13:座標とグラフ
%21C131:参考資料
[1]【中学数学】関数に必要な「座標」ってなにもの??
http://media.qikeru.me/coordinate/
[2]座標 - 中学校数学・学習サイト 勉強法、練習問題プリント
http://math.005net.com/yoten/zahyo.php
[3]中一/座標 no.1
http://www.geisya.or.jp/~mwm48961/math/zahyo01.htm
[4]xy平面上およびxy平面とはどういう意味、概念ですか?本質もおしえて ...
http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1432133764
[5]直交座標系
http://ja.wikipedia.org/wiki/%E7%9B%B4%E4%BA%A4%E5%BA%A7%E6%A8%99%E7%B3%BB
%21C132:座標とグラフ - xy平面の説明は[%21C131].[5]の「平面上の直交座標系」が分り易い(通常は本文のように「x軸」,「y軸」を描く).関数「y=f(x)」のグラフとはxy平面上に点「(x,f(x))」の位置を図示したものである.
/%21C1321:「y=3x」のグラフMS Excelで「Ak」を「0.1*k」,「Bk」を「=3*Ak」にしてグラフを描くと
/
/ - %21C:〔用語・記号〕
- 関数 変数 変域
%21D:D 資料の活用
- %21D1:(1)目的に応じて資料を収集し,コンピュータを用いたりするなどして表やグラフに整理し,代表値や資料の散らばりに着目してその資料の傾向を読み取ることができるようにする。
- ア ヒストグラムや代表値の必要性と意味を理解すること。
- イ ヒストグラムや代表値を用いて資料の傾向をとらえ説明すること。
- %21D:〔用語・記号〕
- 平均値 中央値 最頻値 相対度数 範囲 階級
%21:〔数学的活動〕
- (1) 「A数と式」,「B図形」,「C関数」及び「D資料の活用」の学習やそれらを相互に関連付けた学習において,次のような数学的活動に取り組む機会を設けるものとする。
- ア 既習の数学を基にして,数や図形の性質などを見いだす活動
- イ 日常生活で数学を利用する活動
- ウ 数学的な表現を用いて,自分なりに説明し伝え合う活動
%3: 内容の取扱い
- (1) 内容の「A数と式」の(1)に関連して,数の集合と四則計算の可能性を取り扱うものとする。
- (2) 内容の「A数と式」の(2)のエに関連して,大小関係を不等式を用いて表すことを取り扱うものとする。
- (3) 内容の「A数と式」の(3)のウに関連して,簡単な比例式を解くことを取り扱うものとする。
- (4) 内容の「B図形」の(1)のアに関連して,円の接線はその接点を通る半径に垂直であることを取り扱うものとする。
- (5) 内容の「B図形」の(2)のイについては,見取図,展開図や投影図を取り扱うものとする。
- (6) 内容の「D資料の活用」の(1)に関連して,誤差や近似値,a×10nの形の表現を取り扱うものとする











