G7A%:1小１の算数（改訂版）

%0:%G7A%1:小１の算数（改訂版）
%01:まえがき
=G7A%1:小１の算数（１）＆（２）だの改訂版です．
・本文を読む前にG8E%0:gooブログでの HTML 対策を見てください．
・番号がシアンのパラグラフは現行学習指導要領のコピー．
・番号が薄茶色のパラグラフは追記事項です．
・よく分らない語句や式は無視してください．
%02:目次{}
%03:補遺{}
%04:訂正{}

　%1:目標

（1）具体物を用いた活動などを通して，数についての感覚を豊かにする。数の意味や表し方について理解できるようにするとともに，加法及び減法の意味について理解し，それらの計算の仕方を考え，用いることができるようにする。
（2）具体物を用いた活動などを通して，量とその測定についての理解の基礎となる経験を重ね，量の大きさについての感覚を豊かにする。
（3）具体物を用いた活動などを通して，図形についての理解の基礎となる経験を重ね，図形についての感覚を豊かにする。
（4）　具体物を用いた活動などを通して，数量やその関係を言葉，数，式，図などに表したり読み取ったりすることができるようにする。

　%2:内容

%21A:数と計算

%21A1:（1）ものの個数を数えることなどの活動を通して，数の意味について理解し，数を用いることができるようにする。

ア　ものとものとを対応させることによって，ものの個数を比べること。
イ　個数や順番を正しく数えたり表したりすること。
ウ　数の大小や順序を考えることによって，数の系列を作ったり，数直線の上に表したりすること。
エ　一つの数をほかの数の和や差としてみるなど，ほかの数と関係付けてみること。
オ　2位数の表し方について理解すること。
カ　簡単な場合について，3位数の表し方を知ること。
キ　数を十を単位としてみること。
%21A11:
(1)黄色の四角の中に「●」と「●」がいくつあるでしょう？
・タブレットでは「ゴシック，14pt」が無視されます．
(2)黄色の四角で左から２番目にある「●」はどれでしょう？

　　●　　　●　　　●　　●　　●　　　●　　　　

%21A111:[%21A11]の黄色の四角に「●」が何個（基数）ありますか？
%21A111:A[%21A11]の黄色の四角にある右端の「●」は左端から数えて何番目（序数）になりますか？
%21A12:「⑩」を「10円硬貨」「①」を「1円硬貨」とします．つぎの黄色の四角にあるお金は全部でいくらでしょう？
・

「⑩⑩ ①①①①① ①①」　　

%21A13:つぎの数直線で数の系列「1」「3」「7」の位置はどこでしょう？数「３」（または「7」）は区間「[３]」（または区間「[7]」）の真ん中にかきます．
・N.B.「[３]」は四捨五入すると「３」になる実数の区間です.
[　][１][２][３][４][５][６][７][８][９]
[　　　　　　　　　　　　　　　　　　 ]

%21A14:「①」が多いと数えにくいのでのほかに「5円硬貨」「⑤」も使って考えましょう．
(1)つぎの図を参考にして「27円」「49円」を図で表わしてください．
「38円」＝「⑩⑩⑩⑤①①①」
%21A15:「38円=(3×10＋8)円」は「10」の位（「十」）が「3」，「1」の位（「一」）が「8」の10進数です．これをつぎのようにかきかえてみましょう．
　　　　　「十　　一」
「38円」＝「⑩　　⑤」
　　　　　「⑩　　①」
　　　　　「⑩　　①」
　　　　　「　　　①」

%21A141:「100円硬貨」，「500円硬貨」，「1000円札」，「5000円札」は１文字で表わし難いのでこれらを「(百)」，「(五)」，「|千|」，「|伍|」で表わします．（「伍」）
・e.g.「123円」＝「{百}⑩⑩①①①」

%21A22:(2）加法及び減法の意味について理解し，それらを用いることができるようにする。
         ア　加法及び減法が用いられる場合について知ること。
         イ　1位数と1位数との加法及びその逆の減法の計算の仕方を考え，それらの計算が確実にできること。
        ウ　簡単な場合について，2位数などの加法及び減法の計算の仕方を考えること。/
%21A221:足し算

・「①①」と「①①①」を足したお金は全部で「①①①①①」になります．これを「①①」＋「①①①」＝「⑤」とかきます．つぎの黄色の四角にあるお金は全部で何円になるでしょう？

「①」＋「①」＝「①①」
「①」＋「①①」＝「①①①」
「①①」＋「①①」＝「①①①①」
「①①」＋「①①①」＝「⑤」
「①①①」＋「①①①」＝「⑤①」
「①①①」＋「①①①①」＝「⑤①①」
「①①①①」＋「①①①①」＝「⑤①①①」
「⑤」＋「⑤」＝「⑤⑤」＝「⑩」
「⑤」＋「⑤①」＝「⑤⑤①」＝「⑩①」
「⑤①」＋「⑤①」＝「⑤⑤①①」＝「⑩⑤①①」
「⑤①」＋「⑤①①」＝「⑤⑤①①①」＝「⑩⑤①①①」
「⑤①①」＋「⑤①①」＝「⑤⑤①①①①」＝「⑩①①①①」
「⑤①①」＋「⑤①①①」＝「⑤⑤⑤」＝「⑩⑤」
「⑤①①①」＋「⑤①①①」＝「⑤⑤⑤①」＝「⑩⑤①」
「⑤①①①」＋「⑤①①①①」＝「⑤⑤⑤①①」＝「⑩⑤①①」
「⑤①①①①」＋「⑤①①①①」＝「⑤⑤⑤①①①」＝「⑩⑤①①①」

%21A2211:足し算の表
つぎの表から[ 5]+[ 8]の答えを探してください．[ 5]の行と[ 8]の列の交点が答.
・表が歪むことの対策はG8F%0:gooブログのエディタ（[G8F%31]参照）
・「[5]」を足される数，「[8]」を足す数といいます．
・同じような表は九九にも使います．

[ 0]: [ 1][ 2][ 3][ 4][ 5][ 6][ 7][ 8][ 9]
[ 1]: [ 2][ 3][ 4][ 5][ 6][ 7][ 8][ 9][10]
[ 2]: [ 3][ 4][ 5][ 6][ 7][ 8][ 9][10][11]
[ 3]: [ 4][ 5][ 6][ 7][ 8][ 9][10][11][12]
[ 4]: [ 5][ 6][ 7][ 8][ 9][10][11][12][13]
[ 5]: [ 6][ 7][ 8][ 9][10][11][12][13][14]
[ 6]: [ 7][ 8][ 9][10][11][12][13][14][15]
[ 7]: [ 8][ 9][10][11][12][13][14][15][16]
[ 8]: [ 9][10][11][12][13][14][15][16][17]
[ 9]: [10][11][12][13][14][15][16][17][18]

%21A2212:足し算の表（暗記用）
[ 0]: [ 1][ 2][ 3][ 4][ 5][ 6][ 7][ 8][ 9]
[ 1]: [ 2][ 3][ 4][ 5][ 6][ 7][ 8][ 9][10]
[ 2]: [ 3][ 4][ 5][ 6][ 7][ 8][ 9][10][11]
[ 3]: [ 4][ 5][ 6][ 7][ 8][ 9][10][11][12]
[ 4]: [ 5][ 6][ 7][ 8][ 9][10][11][12][13]
[ 5]: [ 6][ 7][ 8][ 9][10][11][12][13][14]
[ 6]: [ 7][ 8][ 9][10][11][12][13][14][15]
[ 7]: [ 8][ 9][10][11][12][13][14][15][16]
[ 8]: [ 9][10][11][12][13][14][15][16][17]
[ 9]: [10][11][12][13][14][15][16][17][18]

%21A2213:繰り上がりのある足し算
[%21A15]のように（「一」）の位，（「十」）の位に分けて，「38円」＋「7円」の計算について考えてみましょう．

(1)足される額を「38円」足す額を「7円」とします．
(2)「38円」＝「⑩⑩⑩⑤①①①」，「7円」＝「⑤①①」だから
(3)「38円」＋「7円」を[%21A15]のように表現した「1」の位（「一」）のお金は合わせて「⑤①①①」＋「⑤①①」＝「⑩⑤」＝「15円」で，「10」の位（「十」）のお金は「⑩⑩⑩」＝「30円」です．
(4)「15円」は「10円」より多く，「1」の位（「一」）に「⑤⑤」があるので，これを「⑩」と置き換えて「10」の位（「十」）に移動して（繰り上げて），（「十」）の位のお金を「⑩⑩⑩⑩」＝「40円」，（「一」）の位のお金を「⑤」＝「５円」と考えます．
(5)足した結果（総額）は「⑩⑩⑩⑩⑤」＝「45円」
・（「一」）の位のお金を灰色の色紙に，（「十」）の位のお金を茶色の色紙に置いて並べ替えると考え易い．

%21A2214:足し算の筆算
テストでは[%21A2213]のようにお金を使えないので筆算の仕方を考えましょう．

(1)「45円」ー「7円」の場合も[%21A2214]と同様に「十」の位と「一」の位に分けて次のように書きます．

　「十」　「一」
　「３」　「８」　

＋「　」　「７」　　
(2)「8円」＋「7円」＝「15円」であるから（[%21A2211]），「一」の位のお金は「⑤⑤①①①①①」．「⑤⑤」＝「⑩」を「十」の位に繰り上げて，「一」の位のお金は残った「①①①①①」＝「5円」．「十」の位のお金は繰り上げで「１」が増えて「１＋３」＝「４」
　「十」　「一」
・「１」
　「３」　「８」　

＋「　」　「７」　　
・「４」　「５」

(3)答えは「45円」．

%21A222:引き算
・「⑤①①①」ー「[8]」から「①①」＝「[2]」を引いた残りのお金は「⑤①」＝「[6]」になります．これを「[8]」ー「[2]」＝「[6]」とかきます．つぎの黄色の四角にあるお金は全部で何円になるでしょう？
・「[8]」を引かれる数，「[2]」を引く数といいます．
・繰り下がりのあるひき算には，次のような２つの方法があります。
　教科書では，減加法で指導されています。
http://www.shinko-keirin.co.jp/keirinkan/sansu/WebHelp/01/page1_18.html

「⑤⑤」－「　」＝「⑤①①①①①」
「⑤⑤」－「①」＝「⑤①①①①」
「⑤⑤」－「①①」＝「⑤①①①」
「⑤⑤」－「①①①」＝「⑤①①」
「⑤⑤」－「①①①①」＝「⑤①」
「⑤⑤」－「⑤①」＝「①①①①」
「⑤⑤」－「⑤①①」＝「①①①」
「⑤⑤」－「⑤①①①」＝「①①」
「⑤⑤」－「⑤①①①①」＝「①」

%21A2221:引き算の表
つぎの表から[15]ー[ 8]の答えを探してください．[15]の行と[ 8]の列の交点が答.
（繰り下がりのある引き算で使います）．
・[0]は（「x+0=x」「x*0=0」となる）特別な数です．（「0」の扱い）

[20]: [ 1][ 2][ 3][ 4][ 5][ 6][ 7][ 8][ 9]
[19]: [18][17][16][15][14][13][12][11][10]
[18]: [17][16][15][14][13][12][11][10][ 9]
[17]: [16][15][14][13][12][11][10][ 9][ 8]
[16]: [15][14][13][12][11][10][ 9][ 8][ 7]
[15]: [14][13][12][11][10][ 9][ 8][ 7][ 6]
[14]: [13][12][11][10][ 9][ 8][ 7][ 6][ 5]
[13]: [12][11][10][ 9][ 8][ 7][ 6][ 5][ 4]
[12]: [11][10][ 9][ 8][ 7][ 6][ 5][ 4][ 3]
[11]: [10][ 9][ 8][ 7][ 6][ 5][ 4][ 3][ 2]
[10]: [ 9][ 8][ 7][ 6][ 5][ 4][ 3][ 2][ 1]

[ 9]: [ 8][ 7][ 6][ 5][ 4][ 3][ 2][ 1][ 0]
[ 8]: [ 7][ 6][ 5][ 4][ 3][ 2][ 1][ 0][-1]
[ 7]: [ 6][ 5][ 4][ 3][ 2][ 1][ 0][-1][-2]
[ 6]: [ 5][ 4][ 3][ 2][ 1][ 0][-1][-2][-3]
[ 5]: [ 4][ 3][ 2][ 1][ 0][-1][-2][-3][-4]
[ 4]: [ 3][ 2][ 1][ 0][-1][-2][-3][-4][-5]
[ 3]: [ 2][ 1][ 0][-1][-2][-3][-4][-5][-6]
[ 2]: [ 1][ 0][-1][-2][-3][-4][-5][-6][-7]
[ 1]: [ 0][-1][-2][-3][-4][-5][-6][-7][-8]

%21A2223:繰り下がりのある引き算
[%21A15]のように（「一」）の位，（「十」）の位に分けて，「45円」ー「7円」の計算について考えてみましょう．

(1)引かれるお金を「45円」引くお金を「7円」とします．（[%21A2211]）
・%21A22131:「45円」ー「7円」の場合
(3)（「一」）の位のお金は「⑤」＝「5円」
　　（「十」）の位のお金は「⑩⑩⑩⑩」＝「４０円」　
(4)「⑤」から「⑤①①」は引けないので　（「十」）の位の　「⑩⑩⑩⑩」の
「⑩」を「⑤①①①①①」と置換して「これを（「一」）の位に移動する（繰り下げる）
(5)（「一」）の位のお金は「⑤⑤①①①①①」から「⑤①①」を引いた
「⑤①①①」＝「8円」．
（「十」）の位のお金は「⑩⑩⑩⑩」から繰り下げた「⑩」を引いた「⑩⑩⑩」＝「30円」．（分りにくければお金を並べ替えて考えてください）
(6)答えは「⑩⑩⑩」＋「⑤①①①」＝「38円」．

%21A2224:引き算の筆算
(1)「45円」ー「7円」の場合も[%21A2214]と同様に「十」の位と「一」の位に分けて次のように書きます．
　「十」　「一」
　「４」　「５」　
ー「　」　「７」　　　　　　　　　　　　

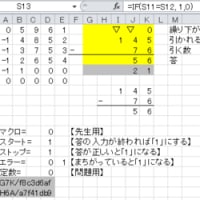
(2)「十」の位の「４」は「10」を「一」の位に繰り下げるので，忘れないように「十」の位に「▽」と書いておきます．
・「▽」は他の文字（e.g.「☆」，「＄」）でもよい．
・他の位から繰り下げる計算（補数による表現）は「小２の算数」で説明します．
　「十」　「一」
　「▽」　「　」　
　「４」　「５」　
ー「　」　「７」　　　

(3)「一」の位に繰り下げた「10」（＝「▽」）から「７」を引いた「3」に引かれる数の「5」と合わせた「8」を「一」の位に書きます．「十」の位の数は「４」から「▽」＝「１」を繰り下げたので「４－１」＝「３」
　「十」　「一」
　「▽」　「　」　
　「４」　「５」　
ー「　」　「７」　
　「３」　「８」　　　　　　　　
(4)答えは「38円」

・旧原稿はG7A%1:小１の算数（２）をご覧ください
aa

	【gooブロガー・先着】dアカウント連携でdポイント2,000pt
	ブログを読むだけ。毎月の訪問日数に応じてポイント進呈
	【コメント募集中】goo blogスタッフの気になったニュース
	gooブロガーの今日のひとこと
	訪問者数に応じてdポイント最大1,000pt当たる！

ぼんさいメモ

介護用ベッドで考えたり、調べたことのメモです。（妻に感謝）
転載：自由（校正・編集不可）。内容：無保証。