垂心四面体ABCDの垂心のベクトルによる重心座標表現で見落としていた大事なこと

「垂心四面体ABCDの[垂心」のベクトルによる重心座標表現で見落としていた大事なこと」　2008.11.03(月)

☆　先に垂心四面体において「内積」に着目して、垂心四面体ABCDの[垂心」の
「ベクトルによる重心座標表現」について述べた。また、別に
三角形の「垂心」の「ベクトルによる重心座標表現」についても、別の
稿で述べた。

◎　もともと、三角形の「垂心・外心」の「ベクトルによる表示」を求めようと
思ったきっかけは、名古屋大学の「栗田　稔」先生が著わされた
数学セミナー増刊　「入門｜現代の数学[７」　具象から幾何学へ」（日本評論社）
を読んでいたら、p54に
「(三角形の）外心や垂心の位置ベクトルを（→OX)＝p(→OA)＋q(→OB)＋r(→OC)
　(p＋q＋r＝１)の形に著わすことは複雑である。」とあったので、
これに触発されて計算したのであった。
計算して割と簡単に「垂心」について「内積」による「ベクトル表示」を得て、これを
「余接」cotを用いて三角関数による表示にし、また「オイラー線の関係」より
「外心」の「ベクトルによる表示」も得ることができ、三角関数の正弦(sin)を用いて表示ができた。
当時「内心」のベクトル表示はしばしば大学入試に出題されていて、「傍心」については、
例えば　石谷　茂　監修　徳峯　良昭　著　「ベクトルとその応用　ー数学ブック6(大阪教育図書)
に載っていて、「内心・傍心」については、知られていたことであった。
それで、「垂心・外心」について発表した。そのとき、「位相幾何学」のホモロジー群の計算に
でてくる「単体の重心座標」の言葉を借用して、「ベクトルによる重心座標表現」の考えの萌芽に
至った。また　名古屋大学の「栗田　稔」先生も同様な研究をされていて、お手紙をいただいた。
「栗田　稔」先生のものは、三辺　a,b,cと角A，B，Cの三角関数の混在したもので、
　同封のコピー用紙に

『任意の点Xの位置ベクトルを
（→OX)＝1/(p＋q＋r)[p(→OA)＋q(→OB)＋r(→OC)]・・・(1)とするとき、

（ア）
　重心G　については、p＝q＝r＝1/3　　　　　　　　　　　　・・・　(1.1.1)
（イ)
　内心　Iについては　p＝a　，q＝b　，r＝c　　　　　　　　・・・(1.1.2)
（ウ
「外心Ｏ」については、p＝acosA，q＝bcosB，ｒ＝ccosC　　・・・(1.1.3)
（イ)
「垂心H」については、ｐ＝asecA、q＝bsecB　、r＝csecC　・・・(1.1.4)
（エ）
　「九点円の中心N」については、
　　p=acos(B－C)　，q=bcos(CーA)　，r＝ccos(A－B)　　・・・(1.1.5)
　
　これらは、次のようにして統一的に導かれる・・・　　　　　　　　　　　　　』
として、図形的に求めておられた。

　さて、私が発表したものを読まれた、「一松　信」先生は、御子息の「明」氏と共に研究されて、
三角形の3辺　a,b,cだけで先の「垂心・外心」を含めて五心について表示され、
「三角形の諸心のベクトル表現」として「一松　明」氏の名前で投稿された。
そのときは、「一松　明」氏のものでは一切、三角関数表示については
触れてはいないので、三角形の「垂心・外心」の「ベクトルによる重心座標表現」の三角関数表示に
ついては、私の方に先行権があるはずである。まあ、そんなことをここで論ずるのではなく、次の

表題の「垂心四面体ABCDの「垂心」のベクトルによる重心座標表現で見落としていた大事なこと」について
触れよう。

☆（１）「(垂心）四面体の「垂心H」のベクトルによる重心座標表現」については、
2008年9月11(木)にBlogに発表したが、
そのとき、
『
四面体ABCDを考える。四面体では一般に、各頂点から対面に引いた４本の垂線は

１点では、交わらない。

この４本の直線が１点で交わるとき、その四面体を「垂心四面体」または

「直辺四面体」といい、その交点Ｈを四面体の「垂心」とよぶ。

　　BC=ａ，CA=b，AB=c，AD=d，BD=e，CD=f　・・・(1.1.7)　とおき、

　　　x=((→AB)，(→AC))=((→AB)，(→AD))=((→AC)，(→AD)) ・・・(1.1.8)　

　　　y=((→BA)，(→BC))=((→BA)，(→BD))=((→BC)，(→BD)) ・・・(1.1.9)

　　　z=((→CA)，(→CB))=((→CA)，(→CD))=((→CB)，(→CD)) ・・・(1.1.10)

　　　w=((→DA)，(→DB))=((→DA)，(→DC))=((→DB)，(→DC)) ・・・(1.1.11）

　　とおく。

このとき、

[命題2]

　　「垂心四面体ABCD」に対して

　　x＋y=c^2，x＋z=b^2,x＋w=d^2，y＋z=a^2，y＋w=e^2，z＋w=f^2　・・・(2.1.1)
　
[定理3]　mをm≧3の自然数、四面体ABCD⊆E^3⊆E^mとし「四面体ABCD」の6辺を

　上の(1.1.7)のように　a，b，ｃ，d，e，fとし、x，y，z，wを上のようにおく。

　PをE^m内の任意の点とすれば、「垂心Ｈ」の「ベクトルによる重心座標表現」は

　(→PＨ)＝1/{detJ(3)}[yzw(→PA)＋xzw(→PB)＋xyw(→PC)＋xyz(→PD)]・・・(3.1.1）
　
　で与えられる。

「命題4.2]　

　「垂心四面体ABCD」に対して6辺を上の(1.1.7)のように

　　　a，b，ｃ，d，e，fとし、　x，y，z，wを(1.1.8)～(1.1.11）のようにおく。

　　　このとき　yzw＋xzw＋xyw＋xyz=detJ(3)　・・・(4.2.1）

　　が成立する。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　』

を発表して、「証明」は後から発表した。

一方　△ABCの「垂心H」については事実を、もっと早く2008.9月の始めに発表して
『
「内積」を用いた表示では、

　　(→ＰＨ)={1/(4・S^2)}×{yz(→ＰＡ)＋xz(→ＰＢ)＋xy(→ＰＣ)}・・・(3)

ここに、
　x=((→ＡＢ)，(→ＡＣ)）,y=((→ＢＡ)，(→ＢＣ)）,z=((→ＣＡ)，(→ＣＢ)）である。


　ただし、((→ＡＢ)，(→ＡＣ)）は(→ＡＢ)と(→ＡＣ)の「内積」を表すものとする。

　　そして　yz＋xz＋xy=4(S^2)　・・・(4)

　　が成立するので、(3)は「ベクトルによる重心座標表現」である。

　また、Sは三角形ＡＢＣの面積である。』　とした。

☆　この、△ABCの「垂心H」の「ベクトルによる重心座標表現」の公式の「証明」が
「まだ現在発表してない」が、容易である。もう少し待っていただきたい。

◎さて、この「垂心四面体」の「垂心」と三角形の「垂心」の２つのことを得た時点で
　次のことに気が付かねばならなかった。

　つまり、「垂心Ｈ」の「ベクトルによる重心座標表現」において、
x=((→AB)，(→AC))=((→AB)，(→AD))=((→AC)，(→AD)) ・・・(1.1.8)　

y=((→BA)，(→BC))=((→BA)，(→BD))=((→BC)，(→BD)) ・・・(1.1.9)

z=((→CA)，(→CB))=((→CA)，(→CD))=((→CB)，(→CD)) ・・・(1.1.10)

w=((→DA)，(→DB))=((→DA)，(→DC))=((→DB)，(→DC)) ・・・(1.1.11）
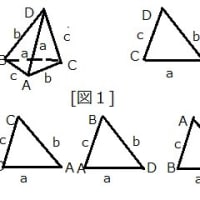
とおいたのだから、△BCD　，△ACD　，△ABD　，△ABCの「垂心」を
それぞれ、H_A　，H_B　，H_C　，H_D、また面積をそれぞれ　S_A　，S_B　，S_C　,S_D
としたとき、例えば
△BCDについては　頂点がB，C,Dであって(1.1.9)から((→BC)，(→BD))＝y ，
(1.1.10)から((→CB)，(→CD))＝z　，(1.1.11）から((→DA)，(→DB))＝wとなっているから、

三角形の「垂心」の表示の公式より、
　(→ＰH_A)=1/{4(S_A)^2}×{zw(→PB)＋yw(PC)＋yz(→PD)}・・・(*)
　かつ、(*)はベクトルによる重心座標表現だから、
　
　4(S_A)^2＝zw＋yw＋yz　・・・(**)　となるわけである。

以上のことより , 次の[定理5.1]が成立するのである。

[定理5.1]
　垂心四面体ABCDにおいて、BC=ａ，CA=b，AB=c，AD=d，BD=e，CD=f　・・・(5.1)　とおき、

　　　x=((→AB)，(→AC))=((→AB)，(→AD))=((→AC)，(→AD)) ・・・(5.1.1)　

　　　y=((→BA)，(→BC))=((→BA)，(→BD))=((→BC)，(→BD)) ・・・(5.1.2)

　　　z=((→CA)，(→CB))=((→CA)，(→CD))=((→CB)，(→CD)) ・・・(5.1.3)

　　　w=((→DA)，(→DB))=((→DA)，(→DC))=((→DB)，(→DC)) ・・・(5.1.4）

　　とおく。
　また、△BCD　，△ACD　，△ABD　，△ABCの「垂心」をそれぞれ、H_A　，H_B　，H_C　，H_D、
　また面積をそれぞれ　S_A　，S_B　，S_C　，S_Dとするとき、
　
(1)　PをE^m内の任意の点とすれば、「垂心四面体ABCD」の「垂心Ｈ」の
　「ベクトルによる重心座標表現」は



　(→PＨ)＝1/{detJ(3)}[yzw(→PA)＋xzw(→PB)＋xyw(→PC)＋xyz(→PD)]　・・・(5.1.5）
　　
　　detJ(3)＝(3!V)^2＝(6V)^2＝yzw＋xzw＋xyw＋xyz　　　　　　・・・(5.1.6)

(2)　PをE^m内の任意の点とすれば、「垂心四面体ABCD」の4つの三角形の面の
　「垂心H_A」,「垂心H_B」，「垂心H_C」　，「垂心H_D」の「ベクトルによる重心座標表現」も
　　求まり、
　 　(→PH_A)＝1/{4(S_A)^2}[zw(→PB)＋yw(→PC)＋yz(→PD)] ・・・(5.2.1)

(→PH_B)＝1/{4(S_B)^2}[zw(→PA)＋xw(→PC)＋xz(→PD)] ・・・(5.2.2)

(→PH_C)＝1/{4(S_C)^2}[yw(→PA)＋xw(→PB)＋xy(→PD)] ・・・(5.2.3)

(→PH_D)＝1/{4(S_D)^2}[yz(→PA)＋xz(→PC)＋xy(→PC)] ・・・(5.2.4)

(3) 面積について

　　4(S_A)^2＝zw＋yw＋yz　・・・(5.3.1)
　　
　　4(S_B)^2＝zw＋xw＋xz　・・・(5.3.2)

4(S_C)^2＝yw＋xw＋xy　・・・(5.3.3)

4(S_D)^2＝yz＋xz＋xy　・・・(5.3.4)

☆　したがって、前に「四面体の垂心・外心の重心座標表現の具体例」をあげたときに、その
　「垂心・外心」またその体積　Vのみなず、
　 側面の「４つの三角形の面積」及び「４つの垂心」もすぐ簡単に計算できたわけであった。