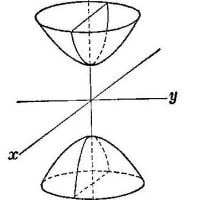
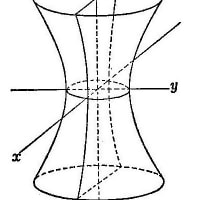
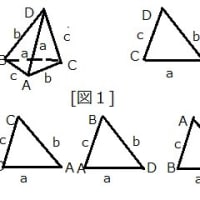
３度の倍数の角の正弦・余弦・正接の真の値と一部のGalois群

３度の倍数の角の正弦・余弦・正接の真の値と一部のGalois群   2021.04.25(日)

　これは at.wikiのホームページ 「もやもやどきどきはらはら」に以前2014年11月2日に掲載したものを

　編集したものです。［少しづつ編集していきます。いろいろあって今は体調が良くないので、

　体調が良くなったら、また少しずつ書き足して行きたいと思います。］

  3°の倍数の角度の正弦、余弦、正接の値は、定規とコンパスにてQ上作図可能ということが知られている。

 これは３６０°の１２０等分ができること、つまり正１２０角形が定規とコンパスで作図できることによる。
 それは120=2³×3×5 であって、3=1+2¹,5=1+2²の奇素数だからである。

 3°の倍数の角の正弦・余弦・正接の真の値のpdfを下のところに載せておきます。

 ここでは、下のpdfに
 sin3° =cos87°,cos3° =sin87°,sin6° =cos84°, cos6°=sin84°,sin9° =cos81°,
 cos9° =sin81°,sin12°=cos78°,cos12°=sin78°,sin15°=cos75°,cos15°=sin75°,
 sin18°=cos72°,cos18°=sin72°,sin21°=cos69°,cos21°=sin69°,
 sin24°=cos66°,cos24°=sin66°,sin27°=cos63°,cos27°=sin63°,sin30°=cos60°,
 cos30°=sin60°,sin33°=cos57°,cos33°=sin57°,sin36°=cos54°,cos36°=sin54°,
 sin39°=cos51°,cos39°=sin51°,sin42°=cos48°,cos42°=sin48°,sin45°=cos45°
 の真の値をまず記す。
 また
 tan(90°-θ)=cotθより、cot(90°-θ) =tanθも出るが、これを使って

 tan3° =cot87°,tan6° =cot84°,tan9° =cot81°,tan12°=cot78°,tan15°=cot75°,
 tan18°=cot72°,tan21°=cot69°,tan24°=cot66°,tan27°=cot63°,tan30°=cot60°,¹
 tan33°=cot57°,tan36°=cot54°,tan39°=cot51°,tan42°=cot48°,tan45°=cot45°,
 tan48°=cot42°,tan51°=cot39°,tan54°=cot36°,tan57°=cot33°,tan60°=cot30°,
 tan63°=cot27°,tan66°=cot24°,tan69°=cot21°,tan72°=cot18°,tan75°=cot15°,
 tan78°=cot12°,tan81°=cot9° ,tan84°=cot6° ,tan87°=cot3°  の
　
 真の値も出てくる。これらの値も下のpdfに書いておいた。計算は2006年までに終了した。

 関数電卓でこれらの値を検算してあるので間違いはないと思う。皆さんも試してください。例えば

 sin6° =[－(√5+1)+√3{√(10－2√5)}]/8 ,

 cos27°=√2{(√5ー1)+√(10+2√5)}/8,

 sin33°=√2{(√3+1)(√5－1)+(√3－1)√(10+2√5)}/16 などと、

 tan9° =(√5+1)－√(5+2√5)…①,   tan27°=(√5－1)－√(5－2√5)…②,

 tan63°=(√5－1)＋√(5－2√5)…③,  tan81°=(√5＋1) ＋√(5+2√5)…④   である。このように、

 ２重根号の組み合わせ、つまり２重根号による逐次拡大の元として表せる。

 これらの形から、ただ、単に計算しただけでなく、Galois群(ガロア群)とその同型対応も、

 考えてみた。

 ただ断っておくが、そのことは一部について計算したのみでその後計算しなかった。

 一例として、xの４次の相反方程式

  x⁴－4x³－14x²－4x＋1=0 ・・・(1) の左辺は有理数体Q上既約で、(1) の

 ４つのQ上の共役解は、

  T={tan81°,－tan27°,tan9°,－tan63°}であり、QにTを添加したQの正規拡大体

 L=Q(tan81°,－tan27°,tan9°,－tan63°)はQ上単純拡大体でガロア拡大となり、

 L=Q(tan81°)=Q(√(5+2√5))となる。また、そのGalois群はZ₄(位数４の巡回群)である。

 そして

 tan27°=－(1/2)tan²81°＋3tan81°＋3/2

 tan63°=－tan³81°＋(9/2)tan²81°＋12tan81°－3/2

 tan9° =－tan³81°＋4tan²81°＋14tan81°＋4

また、方程式(1)の解と係数の関係から、次の一連の等式が成り立つ。

 tan81°－tan27°＋tan9°－tan63°=４…⑤，

 すなわち、tan9°－tan27°－tan63°+tan81°＝４…⑥

  tan81°×(－tan27°)＋tan81°×tan9°＋tan81°×(－tan63°)

 +(－tan27°)×tan9°＋(－tan27°)×(－tan63°)＋tan9°×(－tan63°)

 ＝－１４…⑦　

　つまり、
 
  tan9°×tan27°＋tan9°×tan63°＋tan27°×tan81°＋tan63°×tan81°

 ＝１６…⑧　[　tan81°tan9°＝１，tan27°tan63°＝１　］　

 等が出てくる。

［　あと２つの解と係数の関係式は方程式の相反性などから、⑤と自明なものしか出てこない。］

　また、①～④により、
　
 tan81°＋tan9°＝2(√5＋1)…⑨ ，tan27°＋tan63°＝2(√5－1)…⑩

  ゆえに、tan9°＋tan27°＋tan63°＋tan81°＝4√5 …⑪ ，
　
　tan81°－tan9°＝ 2√(5+2√5)…⑫，tan63°－tan27°＝2√(5－2√5)…⑬
　
 よって、
　
 tan81°－tan9°＋tan63°－tan27°＝2√(5+2√5)＋2√(5－2√5)＝2√(10+2√5)

　すなわち、tan81°－tan9°＋tan63°－tan27°＝2√(10+2√5)…⑭
 
 (∵ pdfの(2.15)式による) も出てくる。

　
 ★ これらについては関数電卓などで検算していただきたい。代数拡大体の理論によれば、

 tan27°,tan63°,tan9°をtan81°の３次以下の多項式として表すときの有理数体Q上の係数は一意的で

 これ以外にはない。これらは大分前に計算したので思い出しながら発表して行きたいと思う。
 
 ☆) pdfの場所→ 3°の倍数の角の正弦・余弦・正接の真の値のpdf  はここからダウンロードしてください。