四面体ABCDの実例で内接球面Iと側面の接点I^Dの重心座標の公式の確認(その1) 2019.05.26(日)
以前、2016.04.25(月)に、blog「物言はぬは腹ふくるる業」で、以下の話題
を扱った。
「四面体の6辺の長さで、二面角の大きさの余弦を表す公式 2016.04.25(月)」
『一般的な四面体の例を挙げ、「重心座標による幾何学」PP225~226の公式を
用いて具体的に、二面角の大きさθ(A,D)を求めよう。なお二面角は内部から測る。
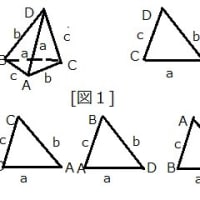
(Ⅰ) 四面体ABCDの6辺を以前のように、BC=a,CA=b,AB=c,AD=d,BD=e,CD=f・・・(1.1)と
おく。[図1参照] また、
△BCD,△ACD,△ABD,△ABCの面積をそれぞれS_A,S_B,S_C,S_D で表す。・・・(1.2)
また便宜上、△BCD,△ACD,△ABD,△ABCそのものも、それぞれS_A,S_B,S_C,S_D で表す。
頂点Aの対面△BCDが S_Aという具合である。二面S_AとS_Dのなす二面角の大きさを
内部から測り、θ(A,D)で表すことにする。内部から測っているから、
0°<θ(A,D)<180°である。もちろん、θ(A,D)=θ(D,A)。そして
四面体ABCDの実例として、
四面体ABCDの6辺を、BC=a=2,CA=b=√7,AB=c=3,AD=d=4,BD=e=√6,CD=f=2√2 ・・・(1.1)
とおく。[図2参照] 』
---という具合だった。
(Ⅱ)このとき、
計算したように、
detJ(3)=149 >0・・・(2.1)。
4S_A=2√23⇔ 2S_A=√23,4S_D=2√27⇔ 2S_D=√27,
4S_C=√5√43=√215 , 4S_B=√223 ・・・(2.2)
また、
cosθ(A,D)=-5/[√23√27]=-0.200643088 位
sinθ(A,D)=2√149/[√23√27] (以前のblog「四面体の正弦定理と応用」より)
θ(A,D) =101.5745676°位 (鈍角!) ・・・(2.3)
また、
cosθ(B,C)=198/[2√223√215]=99/[√223√215]
(blog「物言はぬは腹ふくるる業」による)
sinθ(B,C)=16√149/[√223√215]
θ(B,C) =56.64751355°位 (これらは後の(Ⅲ)の(ア)でも求める)・・・(2.4)である。
次に
(Ⅲ)
cosθ(B,D)を求めよう。「本」のP226の「ややこしい公式(5)」より、
16(S_B)(S_D)cosθ(B,D)
=b^2(f^2+d^2-b^2)+a^2(d^2+b^2-f^2)+c^2(b^2+f^2-d^2)-2b^2e^2 ・・・(3.1)
=f^2(b^2+c^2-a^2)+b^2(c^2+a^2-b^2)+d^2(a^2+b^2-c^2)-2b^2e^2 ・・・(3.2)
(3.1)の右辺は、(1.1)より
=b^2(f^2+d^2-b^2)+a^2(d^2+b^2-f^2)+c^2(b^2+f^2-d^2)-2b^2e^2
=(√7)^2[(2√2)^2+4^2-(√7)^2]+2^2[4^2+(√7)^2-(2√2)^2]+3^2[(√7)^2+(2√2)^2-4^2]
-2×(√7)^2×(√6)^2
=7×(8+16-7)+4×(16+7-8)+9×(7+8-16)-2×7×6
=7×17+4×15+9×(-1)-7×12=119+60-9-84
=86
よって(2.2)を代入して、
cosθ(B,D)=86/[4(S_B)4(S_D)]=86/[√223×2√27]=43/[√223√27] ・・・(3.3)となる。
ついでに sinθ(B,D)を求めよう。「本」のP217の[命題12.25]と同様にして、
sinθ(B,D)=AC√[detJ(3)]/[4(S_B)(S_D)]であるから、
(2.1)(2.2)から、
sinθ(B,D)=AC√[detJ(3)]/[4(S_B)(S_D)]=(√7×√149×2)/[4(S_B)2(S_D)]
=(2√7√149)/[√223×√27] ・・・(3.4)
これらより、θ(B,D)=56.34721356° 位
さて、cosθ(A,D),cosθ(B,D)が求まったので、四面体の第1余弦定理
S_D=(S_A)cosθ(A,D)+(S_B)cosθ(B,D)+(S_C)cosθ(C,D) ・・・(3.5)から、cosθ(C,D)を
求めることが できる。(2.2)及び(2.3)と(3.3)を、(3.5)を4倍したものに代入すれば、
2√(27)=2√23×{-5/[√23√27]}+√223×{43/[√223√27]}
+√215×cosθ(C,D)
√215×cosθ(C,D)=2√27-2×{-5/[√27]}-{43/√27}
=2√27-33/[√27]
この両辺を√27倍して、√27√215×cosθ(C,D)=2×27-33
⇔ cosθ(C,D)=21/[√27√215] ・・・(3.6) となる。こうして、
二面角 、θ(A,D),θ(B,D),θ(C,D)の余弦が求まった。[ Dがみな付いている事に注意]
☆ すると3つの四面体の第3余弦定理から、
cosθ(B,C),cosθ(A,C),cosθ(A,B)が求まるのである。こうして
6つの二面角の余弦 cosθ(A,D),cosθ(B,D),cosθ(C,D),cosθ(B,C),cosθ(A,C),cosθ(A,B)
が全て求まる。これを実行しよう。
(ア) まず第3余弦定理 (S_A)^2+(S_D)^2-2(S_A)(S_D)cosθ(A,D)
=(S_B)^2+(S_C)^2-2(S_B)(S_C)cosθ(B,C)
により、cosθ(A,D)からcosθ(B,C)を求める。
上の式を16倍すると、
(4S_A)^2+(4S_D)^2-2(4S_A)(4S_D)cosθ(A,D)
=(4S_B)^2+(4S_C)^2-2(4S_B)(4S_C)cosθ(B,C)
これに、(2.2)(2.3)を代入して
(2√23)^2+(2√27)^2-2(2√23)(2√27){-5/[√(23)√(27)]}
=(√223)^2+(√215)^2-2(√223)(√215)cosθ(B,C)
⇔ 2(√223)(√215)cosθ(B,C)=223+215-(4×23+4×27+8×5)
=223+215-(92+108+40)
=223+215-200-40=23+175
=198
よって cosθ(B,C)=99/[√223√215] ・・・(3.7)
(イ)
次に第3余弦定理 (S_B)^2+(S_D)^2-2(S_B)(S_D)cosθ(B,D)
=(S_A)^2+(S_C)^2-2(S_A)(S_C)cosθ(A,C)
により、cosθ(B,D)からcosθ(A,C)を求める。これは16倍した
(4S_B)^2+(4S_D)^2-2(4S_B)(4S_D)cosθ(B,D)
=(4S_A)^2+(4S_C)^2-2(4S_A)(4S_C)cosθ(A,C) と同値。
これに、(2.2)(3.3)を代入して
(√223)^2+(2√27)^2-2(√223)(2√27)×{43/[√223√27]}
=(2√23)^2+(√215)^2-2(2√23)(√215)cosθ(A,C)
⇔ 2(2√23)(√215)cosθ(A,C)=4×23+215-(223+4×27-4×43)
=92+215-(223+108-172)
=92+215-223-108+172
=(92-108)+(215-223)+172
=-16-8+172
=-24+172=148
よって cosθ(A,C)=37/[√23√215] ・・・(3.8)
(ウ)
最後に 第3余弦定理 (S_C)^2+(S_D)^2-2(S_C)(S_D)cosθ(C,D)
=(S_A)^2+(S_B)^2-2(S_A)(S_B)cosθ(A,B)
により cosθ(C,D)からcosθ(A,B)を求める。これは16倍した
(4S_C)^2+(4S_D)^2-2(4S_C)(4S_D)cosθ(C,D)
=(4S_A)^2+(4S_B)^2-2(4S_A)(4S_B)cosθ(A,B) と同値。
これに、(2.2)(3.6)を代入して
(√215)^2+(2√27)^2-2(√215)(2√27)×{21/[√215√27]}
=(2√23)^2+(√223)^2-2(2√23)(√223)cosθ(A,B)
⇔ 2(2√23)(√223)cosθ(A,B)=(4×23+223)-(215+4×27-4×21)
=92+223-(215+108-84)
=223-215-108+84+92
=8-108+176=76
よって cosθ(A,B)=19/[√23√223] ・・・(3.8)
以上(ア)(イ)(ウ)により、四面体ABCDの6つの二面角の余弦が全て求まった。
二面角は全て、0°より大きく180°より小さいので、二面角の余弦から、全て
求まるわけである。以上を含めて、二面角の正弦も全て求めて一覧にしてまとめておく。
(Ⅳ)
BC=a=2,CA=b=√7,AB=c=3,AD=d=4,BD=e=√6,CD=f=2√2 のとき、四面体ABCDが
できる。
detJ(3)=149, 4S_A=2√23,4S_B=√223,4S_C=√215,4S_D=2√27
そして四面体ABCDの体積をVとするとき、6V=√detJ(3)=√149 ・・・(4.1)となる。
(1) cosθ(A,D)=-5/[√23√27]=-0.200643088 位 ・・・(4.1.1)
sinθ(A,D)=2√149/[√23√27] ・・・(4.1.2)
θ(A,D) =101.5745676°位 (鈍角!) ・・・(4.1.3)
(2) cosθ(B,D)=43/[√223√27] ・・・(4.2.1)
sinθ(B,D)=2√7√149/[√223×√27] ・・・(4.2.2)
θ(B,D) =56.34721355°位 ・・・(4.2.3)
(3) cosθ(C,D)=21/[√27√215] = ・・・(4.3.1)
sinθ(C,D)=6√149/[√27√215] ・・・(4.3.2)
θ(C,D) =74.00075251° 位 ・・・(4.3.3)
(4) cosθ(B,C)=99/[√223√215] ・・・(4.4.1)
sinθ(B,C)=16√149/[√223√215] ・・・(4.4.2)
θ(B,C) =63.11956117° 位 ・・・(4.4.3)
(5) cosθ(A,C)=37/[√23√215] ・・・(4.5.1)
sinθ(A,C)=2√6√149/[√23√215] ・・・(4.5.2)
θ(A,C) =58.25357225° 位 ・・・(4.5.3)
(6) cosθ(A,B)=19/[√23√223] ・・・(4.6.1)
sinθ(A,B)=4√2√149/[√23√223] ・・・(4.6.2)
θ(A,B) =74.61522034° 位 ・・・(4.6.3)
☆☆
ここで 求め方の注意。
まず、二面角 θ(A,D),θ(B,D),θ(C,D),θ(B,C),θ(A,C),θ(A,B)の中で、
二面角の2つの添え字の内、1つずつ共通な文字の「余弦」を「本」P225からP226
の「ややこしい」公式で、2つ求める。[先ほどの例では,θ(A,D)とθ(B,D)のDが共通]
そのあとは覚えやすい四面体の第1余弦定理で、共通な文字を添え字にもつ
残りの二面角の余弦をまず求める。[先ほどの例では、θ(C,D)の余弦を求める。]
次に、四面体の第3余弦定理を3回使用して、2つの添え字に共通な文字がない
二面角の余弦を3つ求めると良い。[先ほどの例ではcosθ(A,D)→cosθ(B,C)。
cosθ(B,D)→cosθ(A,C)。cosθ(C,D)→cosθ(A,B)。のように求めるということ。]
二面角の正弦については、detJ(3)、言い換えれば四面体ABCDの体積Vが求まって
いれば、「本」の「四面体ABCDの二面角の正弦の公式」P217の[命題12.25]の
sinθ(A,D)=BC√detJ(3)/[4(S_A)(S_D)] などで、求めるのが簡単である。
[なお、四面体の第2余弦定理を使って、θ(A,D),θ(D,B)から、θ(B,A)を求めても
よいが、計算が大変である。ただし、この場合の第2余弦定理とは、
(S_C)^2=(S_A)^2+(S_D)^2+(S_B)^2
-2(S_A)(S_D)cosθ(A,D)-2(S_D)(S_B)cosθ(D,B)-2(S_B)(S_A)cosθ(B,A)
をさす。添え字A,D,Bが巡回的]
☆☆
求め方の注意終わり。
ーーーーーーーーーー四面体ABCDの実例で内接球面Iと側面の接点I^Dの重心座標の公式の確認 (その2)へ続くーーーーー










![四面体ABCDの「内接球面Iの接点」と内心Iとの間のベクトル等式_[その1]](https://blogimg.goo.ne.jp/image/upload/f_auto,q_auto,t_image_square_m/v1/user_image/5e/ac/2ca05906d9b1993ea5acd407785ebac4.jpg)