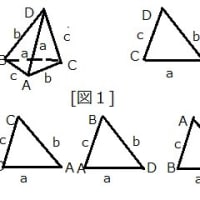
垂心四面体ABCDの各頂点から対面の三角形に下した垂線の足はその三角形の垂心

「垂心四面体ABCD」の各頂点から対面の三角形に下した垂線の足はその「三角形の垂心」2008.11.2(日)

(1)　例によって　、BC＝a　，CA＝b，　AB＝c，BD=e　，CD＝f　とし
　　　x=([→AB]，[→AC])=([→AB]，[→AD])=([→AC]，[→AD]) ・・・(1.1.1)　

　　　y=([→BA]，[→BC])=([→BA]，[→BD])=([→BC]，[→BD]) ・・・(1.1.2)

　　　z=([→CA]，[→CB])=([→CA]，[→CD])=([→CB]，[→CD]) ・・・(1.1.3)

　　　w=([→DA]，[→DB])=([→DA]，[→DC])=([→DB]，[→DC]) ・・・(1.1.4）

　　とおく。detJ(2)は、(→AB)と(→AC)のGramの行列式であり、detJ(3)は
　　(→AB)，(→AC)，(→AD)のGramの行列式とする。detJ(2)>0　，detJ(3)>0　である。

(2)　表題の事実は、「三垂線の定理」を用いて「証明」ができる。
　　
　すなわち　次の「命題1.1」が成立する。
　[命題1.1]
　　「垂心四面体ABCD」において、頂点Dから、対面の△ABCに下した「垂線の足」K_Dは△ABCの
　　「垂心H_D」になる。
　「証明」　　
　　まず、K_D≠Aのときを考える。このとき、　BC⊥A(K_D)　・・・(1.1.5)を示そう。
　　
　　BC⊥D(K_D)　・・・(1.1.6)である。また「垂心四面体ABCD」の条件　BC⊥DA　から
　　BC⊥△DA(K_D)　よって　BC⊥A(K_D)　　　[注意：これが「三垂線の定理」の1つの型である]
　　同様にして、K_D≠B　，K_D≠C　のときは、　
　　CA⊥B(K_D)・・・(1.1.7)，　AB⊥C(K_D)・・・(1.1.8)
　　(a)　ゆえに、K_Dが△ABCの頂点　A,B,Cのどれにも一致しないときは、(1.1.5)と(1.1.7)(1.1.8)
　　　から、点　K_Dは△ABCの「垂心H_A」になる。
　　(b)　K_Dが△ABCの頂点　A,B,Cのどれかに一致するとき、例えばK_D=Aのとき、
　　　　K_D≠B，かつ　K_D≠Cとなるから、上の(a)から　
　　　CA⊥(BK_D)・・・(1.1.8)，　AB⊥(CK_D)・・・(1.1.9がいえている。
　　　K_D=Aだから　これらは、　　　CA⊥BA　　，AB⊥CA　となる。
　　つまりAB⊥AC　　よって△ABCは、∠BAC＝90度の「直角三角形ABC」になる。
　　この「直角三角形ABC」の「垂心H_D」は明らかに、「頂点A」である。
　　　K_D=Aだから、頂点Dから、対面の△ABCに下した「垂線の足」K_Dは△ABCの
　　「垂心H_D」＝「頂点A」になる。
　なお、このとき、DK_D⊥△ABCより、DA⊥△ABCとなる、よって、K_D=Aのときは
　この「垂心四面体ABCD」は「A－3直角四面体」となり、その「四面体」としての
　「垂心H」＝「頂点A」であることも分かる。
　（「命題1.1」の証明終わり）
☆　この「命題1.1」の証明の(b)の部分を
　[命題1.2]として掲げておこう。

　[命題1.2]
　　「垂心四面体ABCD」において、頂点Dから対面の△ABCに下した「垂線」の足が
　　　△ABCの「頂点Aに一致」
　　⇒　この「垂心四面体ABCD」は「A－3直角四面体」である。つまり、
　　　　「垂心四面体ABCD」の「垂心H」は「頂点A」である。

☆　さて、
「命題1.1」は、「頂点D」が「垂心四面体ABCD」の「垂心H」と異なるときには
「ベクトルによる重心座標表現」の公式から、計算によって示すことができる。

まず、次のことに注意しよう。前にBlogの「重心座標表現の具体例_第5(3直角四面体の場合）」で
　述べたことの否定命題を考えて
　[命題1.3]
　「頂点D」が「垂心四面体ABCD」の「垂心H」と異なる　
　　　　⇔　D≠H　　・・・(1.3.1)
　　　　⇔　w≠0　　・・・(1.3.2)　　（ｗは上の(1)の(1.1.4）のものである）
　　　　⇔「垂心四面体ABCD」は「Dー3直角四面体」ではない　　・・・(1.3.3)
◎これを用いて「頂点D」が「垂心四面体ABCD」の「垂心H」と異なるときには、
　計算で「命題1.1]を「証明できる」
　[命題1.4]
　　「頂点D」が「垂心四面体ABCD」の「垂心H」と異なる「垂心四面体ABCD」に
　　おいて、「頂点D」から対面の△ABCに下した垂線の足K_Dは、
　△ABCの「垂心H_D」である。つまり直線DHと△ABCを含む平面との交点は
　　△ABCの「垂心H_D」である。
　「証明」
　「垂心四面体ABCD」の「垂心H」の「ベクトルによる重心座標表現」は
　任意の点P∈E^m　(mは3以上の自然数）に対して
　(→PＨ)＝1/{detJ(3)}[yzw(→PA)＋xzw(→PB)＋xyw(→PC)＋yzw(→PD)]・・・(1.4.1）

　また、△ABCの「垂心H_D」のベクトルによる重心座標表現」は△ABCを
　考えているから、　x，y，zを用いて

　(→PＨ_D)＝1/{detJ(2)}[yz(→PA)＋xz(→PB)＋xy(→PC))]　・・・(1.4.2）

　ここに　detJ(2)は、(→AB)と(→AC)からできるGramの行列式であって、
　S_Dを△ABCの面積としたとき、detJ(2)＝yz+xz＋xy＝4(S_D)^2　・・・(1.4.3）
　であるから、
　
　(→PＨ_D)＝[yz(→PA)＋xz(→PB)＋xy(→PC))]/(yz＋xz＋xy)　・・・(1.4.4)ともなる。

さて、D，H，K_Dは一直線上にあるから、(→DH)＝(1－t)(→DK_D)　・・・(1.4.5)
　となる実数　tがただ一つ存在する。
　
　κ＝(yzw)/{detJ(3)} ，λ＝(xzw)/{detJ(3)}　，
　μ＝(xyw)/{detJ(3)}　，ν＝(xyz)/{detJ(3)}　・・・(1.4.6）として、
　(1.4.1）は(→PH)＝κ(→PA)＋λ(→PB)＋μ(→PC)＋ν(→PD)　・・・(1.4.7）
　かつ　κ＋λ＋μ＋ν＝1　・・・(1.4.8)　となる。よって
　t＝ν　・・・(1.4.9)となり、
（t＝ν　・・このことについてはまた別の機会に示す。垂心Hに限ったことではない。
　　重心座標表現において一般的に成り立つことである　。　　　　　　　　　　　　　　）
　(1.4.5)は　
(→PH)－(→PD)＝(1－ν){(→PK_D)－(→PD)}
⇔　(→PH)＝ν(→PD)＋(1－ν)(→PK_D)　・・・(1.4.10)
　ゆえに　垂心Hは、線分DK_Dを　(1－ν)：νの比に分ける点である。
　
よって　D≠H　⇔　1－ν≠0　⇔　ν≠1　・・・(1.4.11)である。
　(1.4.10)と(1.4.7）から　
(1－ν)(→PK_D)＝(→PH)－ν(→PD)＝κ(→PA)＋λ(→PB)＋μ(→PC)
ここで　D≠H　より、ν≠1　よって
　(→PK_D)＝1/(1－ν)［κ(→PA)＋λ(→PB)＋μ(→PC)]　・・・(1.4.11)
　(1.4.6)から　κ＋λ＋μ＝1－ν≠0　で(1.4.11)は
　(→PK_D)＝[κ(→PA)＋λ(→PB)＋μ(→PC)]/(κ＋λ＋μ)　・・・(1.4.12)
　　となる。(1.4.6)　から

　κ＋λ＋μ＝(yzw＋xzw＋xyw)/{detJ(3)}＝w(yz＋xz＋xy)/{detJ(3)}　・・・(1.4.13)
　また　κ(→PA)＋λ(→PB)＋μ(→PC)
　＝1/{detJ(3)}[yzw(→PA)＋xzw(→PB)＋xyw(→PC)]
　＝w/{detJ(3)}[yz(→PA)＋xz(→PB)＋xy(→PC)]　・・・(1.4.14)
　よって　(1.4.12)は　w≠0　から
　(→PK_D)＝w[yz(→PA)＋xz(→PB)＋xy(→PC)]/｛w(yz＋xz＋xy)}
　　　　　＝[yz(→PA)＋xz(→PB)＋xy(→PC)]/(yz＋xz＋xy) ・・・(1.4.15) となった。
　(1.4.4)と(1.4.15)から
　(→PＨ_D)＝(→PK_D)　⇔　K_D＝H_D
　
ゆえに　「頂点D」が「垂心四面体ABCD」の「垂心H」と異なる「垂心四面体ABCD」
において、「頂点D」から対面の△ABCに下した垂線の足K_Dは
　△ABCの「垂心H_D」であることが、計算で示された。
　（証明終わり）