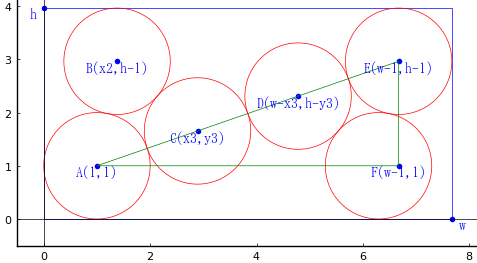
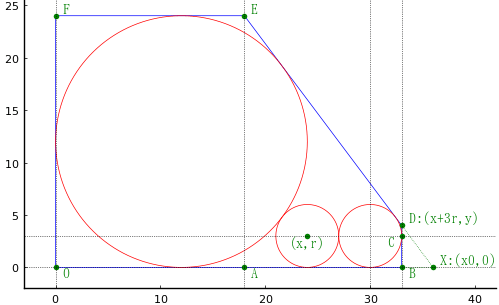
算額(その129)
千葉県市原市 薬王寺 寛政元年(1789)
https://fururen.net/siryoukan/bunkazai/bunkazaisitu.htm
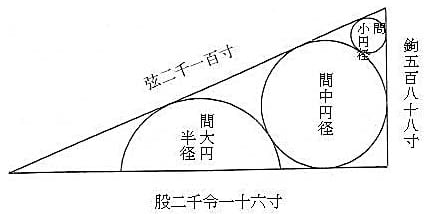
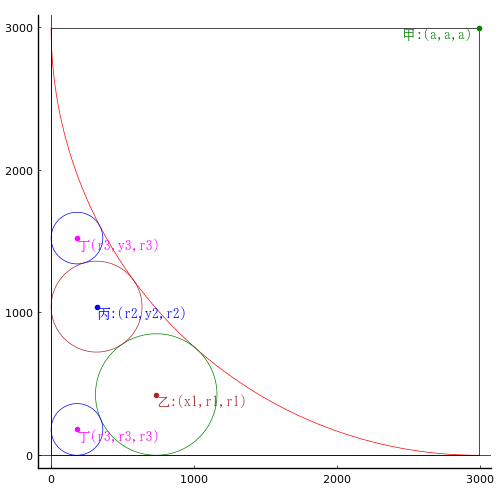
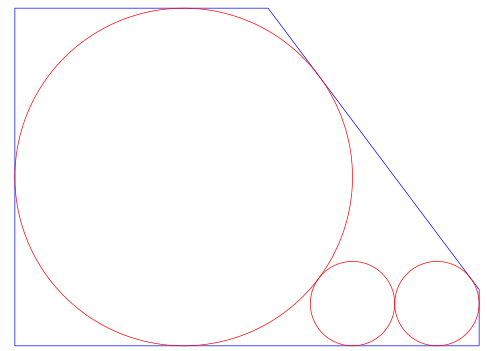
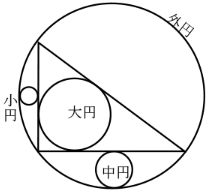
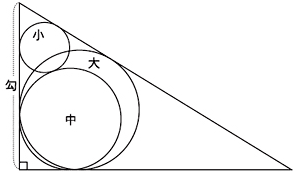
鉤股弦をそれぞれ,588, 2016, 2100 とし,また以下のように記号を定め,方程式を立てて,解く。
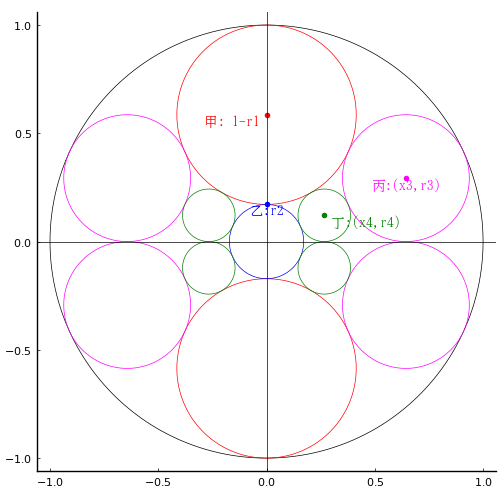
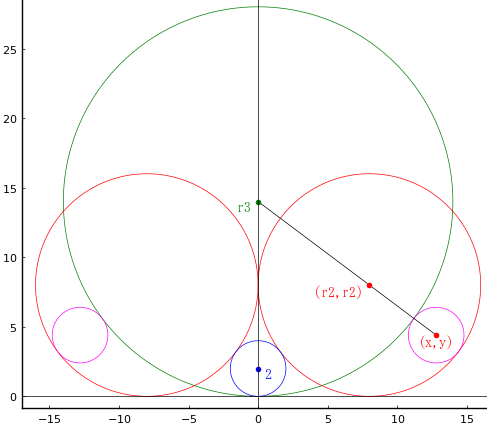
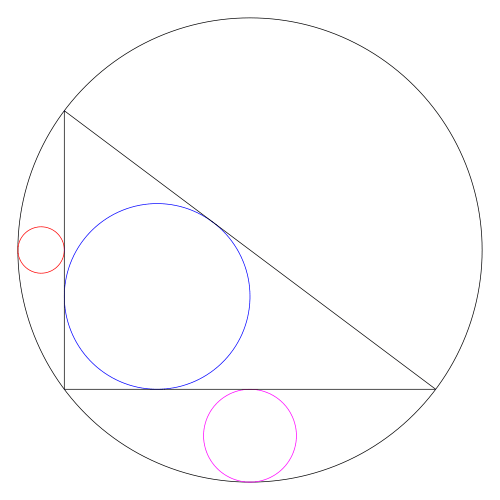
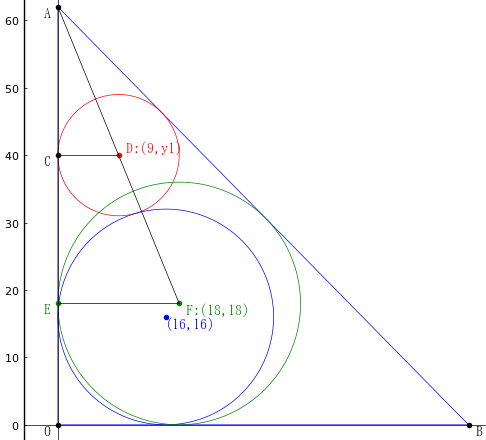
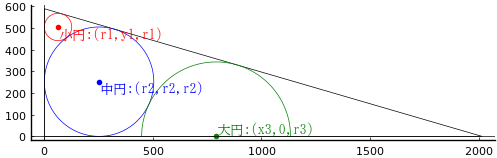
小円の中心座標,半径 r1, y1, r1
中円の中心座標,半径 r2, r2, r2
大円の中心座標,半径 x3, 0, r3
using SymPy
function distance(x1, y1, x2, y2, x0, y0)
p1, p2 = sympy.Point(x1, y1), sympy.Point(x2, y2)
l = sympy.Line(p1, p2)
l.distance(sympy.Point(x0, y0))^2 # 二乗距離を返す!!
end;
@syms r1::positive, y1::positive, r2::positive, x3::positive, r3::positive;
eq1 = (r1-r2)^2 + (y1 - r2)^2 - (r1 + r2)^2 # 小中
eq2 = (r2 - x3)^2 + r2^2 - (r2 + r3)^2 # 中大
eq3 = distance(2016, 0, 0, 588, r1, y1) - r1^2 # 小円の中心から斜辺への距離
eq4 = distance(2016, 0, 0, 588, r2, r2) - r2^2 # 中円の中心から斜辺への距離
eq5 = distance(2016, 0, 0, 588, x3, 0) - r3^2; # 大円の中心から斜辺への距離
res = solve([eq1, eq2, eq3, eq4, eq5], (r1, y1, r2, x3, r3))
8-element Vector{NTuple{5, Sym}}:
(63, 504, 252, 791, 343)
(784/3, 784, 2352, 1666, 98)
(784/3, 784, 2352, 6223/3, 49/3)
(784/3, 784, 2352, 4116, 588)
(448, 924, 252, 791, 343)
(21168, 16464, 2352, 1666, 98)
(21168, 16464, 2352, 6223/3, 49/3)
(21168, 16464, 2352, 4116, 588)
y1 < 588 でなければならないので,1 番目以外の解は不適切である。
for i = 1:8
if res[i][2] < 588
println("\ni = $i")
for j = 1:5
println("$j $(res[i][j].evalf())")
end
end
end
i = 1
1 63.0000000000000
2 504.000000000000
3 252.000000000000
4 791.000000000000
5 343.000000000000
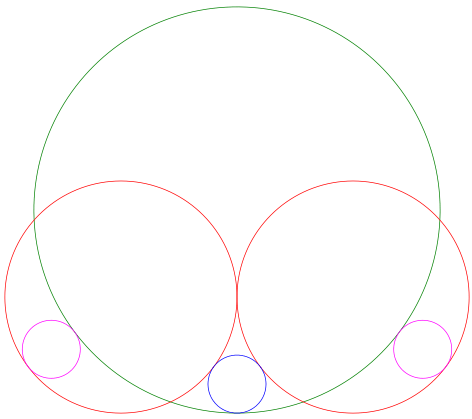
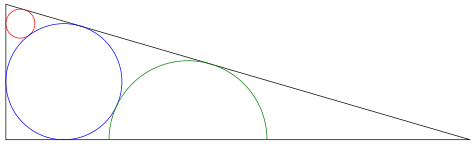
r1 = 63.000; y1 = 504.000; r2 = 252.000; x3 = 791.000; r3 = 343.000 となる。
求められている小円の径は 63*2 = 126寸,中円の径は 252*2 = 504寸,大円の半径はそのまま 343寸である。
using Plots
using Printf
function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
θ = beginangle:0.1:endangle
x = r.*cosd.(θ)
y = r.*sind.(θ)
plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;
function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
mark && scatter!([x], [y], color=color, markerstrokewidth=0)
annotate!(x, y, text(string, 10, position, color, vertical))
end;
function draw(more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r1, y1, r2, x3, r3) = res[1]
@printf("r1 = %.3f; y1 = %.3f; r2 = %.3f; x3 = %.3f; r3 = %.3f\n",
r1.evalf(), y1.evalf(), r2.evalf(), x3.evalf(), r3.evalf())
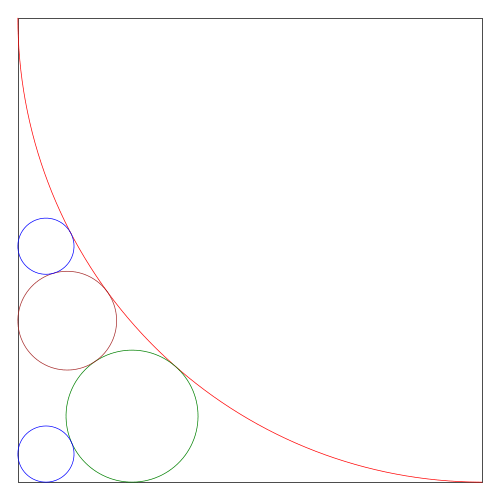
plot([0, 2016, 0, 0], [0, 0, 588, 0], color=:black, lw=0.5)
circle(r1, y1, r1)
circle(r2, r2, r2, :blue)
circle(x3, 0, r3, :green, beginangle=0, endangle=180)
if more == true
point(r1, y1, "小円:(r1,y1,r1)", :red)
point(r2, r2, "中円:(r2,r2,r2)", :blue)
point(x3, 0, "大円:(x3,0,r3)", :green, :left, :bottom)
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;
r1 = 63.000; y1 = 504.000; r2 = 252.000; x3 = 791.000; r3 = 343.000