算額(その122)
一関市博物館 > 和算に挑戦 > 令和元年度出題問題(2) [中級問題](中学・高校生向き)
岩手県一関市舞川の菅原神社に嘉永3年(1850)に奉納された算額
https://www.city.ichinoseki.iwate.jp/museum/wasan/r1/normal.html
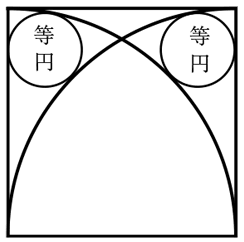
正方形の内部に四分円を配置し等円が 2 個入っている。等円の直径が一寸のとき,黒く塗った部分の面積はいかほどか。
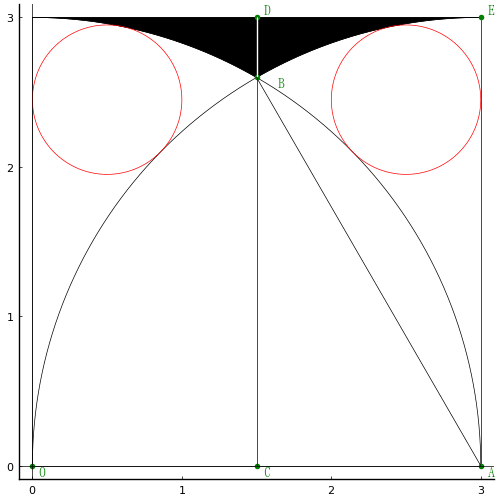
正方形の一辺の長さを a,右の等円の中心座標を (a - 1/2, y) とする。四分円と等円が接することから 2 本の方程式を立て,解く。
using SymPy
@syms a, y;
eq1 = (a - 1//2)^2 + y^2 - (a +1//2)^2
eq2 = (1//2)^2 + y^2 - (a - 1//2)^2
res = solve([eq1, eq2], (a, y))
3-element Vector{Tuple{Sym, Sym}}:
(0, 0)
(3, -sqrt(6))
(3, sqrt(6))
res |> println
Tuple{Sym, Sym}[(0, 0), (3, -sqrt(6)), (3, sqrt(6))]
a = 3, y = sqrt(6) が適切な解である。すなわち,正方形の一辺の長さは元の単位で 3 寸である。
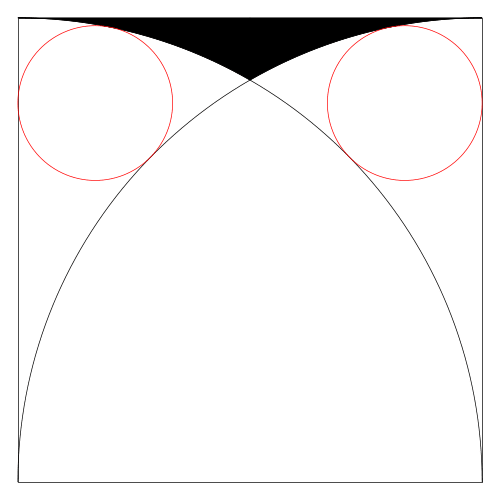
using Plots
using Printf
function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
θ = beginangle:0.1:endangle
x = r.*cosd.(θ)
y = r.*sind.(θ)
plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;
function circle(ox, oy, r, color=:red; beginangle=0, endangle=360, fill=false)
θ = beginangle:0.1:endangle
x = r.*cosd.(θ)
y = r.*sind.(θ)
if fill
plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5, seriestype=:shape, fillcolor=color)
else
plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end
end;
function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
mark && scatter!([x], [y], color=color, markerstrokewidth=0)
annotate!(x, y, text(string, 10, position, color, vertical))
end;
function segment(x1, y1, x2, y2, color=:black; linestyle=:solid, linewidth=0.5)
plot!([x1, x2], [y1, y2], color=color, linestyle=linestyle, linewidth=linewidth)
end;
function blackarea(ox, oy, a, color=:black; beginangle=0, endangle=360)
θ = beginangle:0.1:endangle
x = a * cosd.(θ); append!(x, x[1]); append!(x, x[1])
y = a * sind.(θ); append!(y, y[end]); append!(y, y[1])
plot!(ox .+ x, oy .+ y, color=color, seriestype=:shape, fillcolor=color, lw=0.5)
x = a .- x[end:-1:1]
y = y[end:-1:1]
plot!(ox .+ x, oy .+ y, color=color, seriestype=:shape, fillcolor=color, lw=0.5)
end
function draw(more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(a, y) = (3, sqrt(6))
println("(a, y) = $((a, y))")
plot([0, a, a, 0, 0], [0, 0, a, a, 0], color=:black, lw=0.5)
blackarea(0, 0, a, :black, beginangle=60, endangle=90)
circle(0, 0, a, :black, beginangle=0, endangle=90)
circle(a, 0, a, :black, beginangle=90, endangle=180)
circle(a - 1/2, y, 1/2, :red)
circle(1/2, y, 1/2, :red)
if more == true
point(a/2, a√3/2, " B")
point(0, 0, " O")
point(a/2, 0, " C")
point(a, 0, " A")
point(a/2, a, " D", :green, :left, :bottom)
point(a, a, " E", :green, :left, :bottom)
segment(a/2, a√3/2, a/2, a, :white, linewidth=1)
segment(a/2, a√3/2, a, 0, :black)
segment(a/2, a√3/2, a/2, 0)
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;
(a, y) = (3, 2.449489742783178)
長方形 ACDE の面積 = X = a^2 / 2,扇形 ABE の面積 = Y = a^2 * pi / 12,三角形 ABC の面積 = Z = (a/2)^2 * sqrt(3) / 2
黒く塗った部分の半分 BDE の面積 = X - Y - Z
黒く塗った部分の面積は 2(X - Y - Z) = 0.39049670258533675
2(a^2 / 2 - a^2 * pi / 12 - (a/2)^2 * sqrt(3) / 2)
@syms a
eq = 2(a^2 // 2 - a^2 * PI / 12 - (a/2)^2 * sqrt(Sym(3)) / 2);
simplify(eq) |> println
a^2*(-pi/6 - sqrt(3)/4 + 1)
SymPy の integrate() で解いてみよう。
using SymPy
@syms x
2integrate(3-sqrt(9 - x^2), (x, 0, 1.5))
0.390496702585335


















