算額(その121)
一関市博物館 > 和算に挑戦 > 令和2年度出題問題(2) [中級問題](中学・高校生向き)
岩手県一関市の伊吹神社に明治17年(1884)に奉納された算額より
https://www.city.ichinoseki.iwate.jp/museum/wasan/r2/normal.html
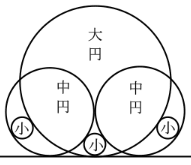
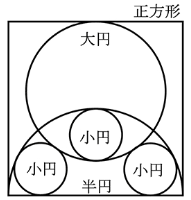
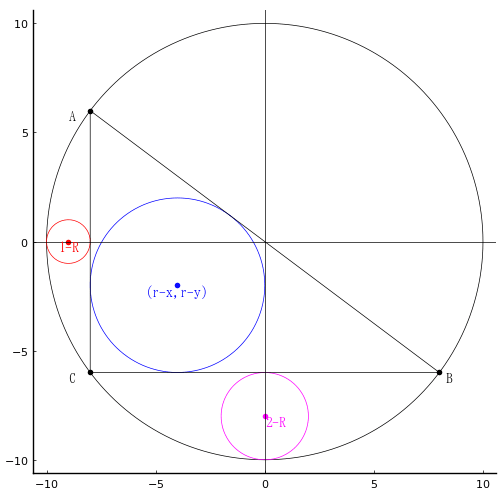
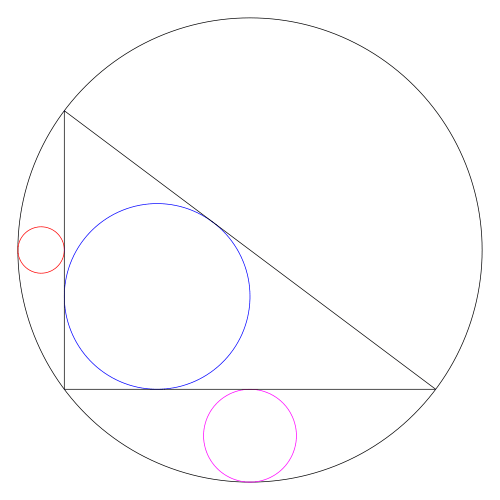
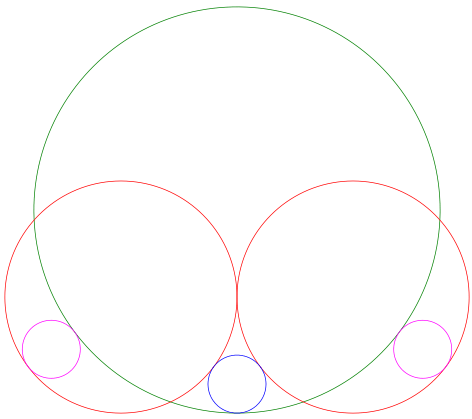
図のように大円,中円,小円が配置されている。大円の中心と右側(左側)の中円,小円の中心は一直線上にある。小円の直径が 2 寸のとき,大円の直径はいかほどか。
出題は円の直径であるが,小数点がつかないように2倍して半径を用いる。また,昨図のために必要な座標をすべて求める。
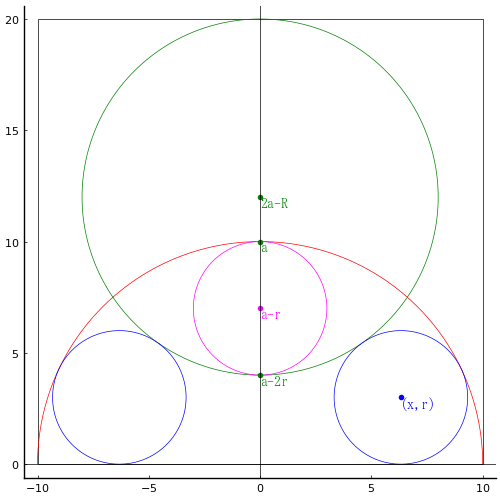
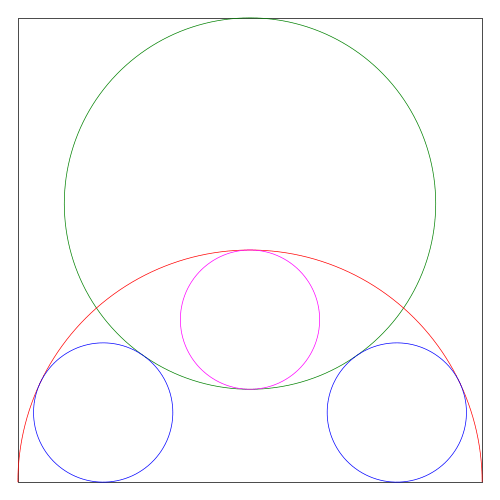
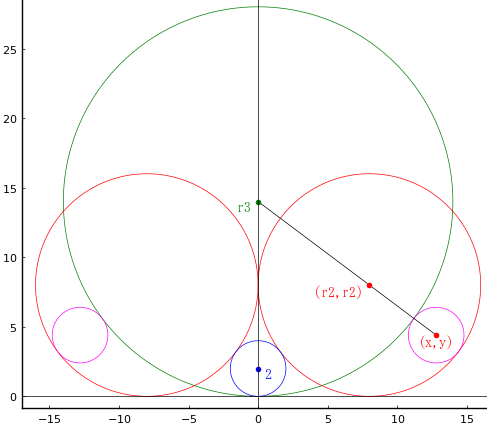
大円の,中円の半径を r3, r2 とする。右の小円の中心座標を (x, y) とする。図のように記号を定め,方程式を解く。
using SymPy
@syms x, y, r1, r2, r3;
eq1 = r2^2 + (r2 - 2)^2 - (2 + r2)^2
eq2 = (x - r2)^2 +(r2 - y)^2 - (r2 - 2)^2
eq3 = x^2 + (r3 - y)^2 - (r3 + 2)^2
eq4 = (r3 - r2)^2 + r2^2 - r3^2
eq5 = (r3 - r2) * (x - r2) - (r2 - y) * r2
res = solve([eq1, eq2, eq3, eq5], (x, y, r2, r3))
2-element Vector{NTuple{4, Sym}}:
(16/5, 22/5, 8, 2)
(64/5, 22/5, 8, 14)
2 組目が適切な解である。
大円の半径が 14 で,元の単位では直径が 14 寸である。
中円の直径が 8 寸,右の小円の中心座標が (64/5, 22/5) である。
using Plots
using Printf
function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
θ = beginangle:0.1:endangle
x = r.*cosd.(θ)
y = r.*sind.(θ)
plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;
function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
mark && scatter!([x], [y], color=color, markerstrokewidth=0)
annotate!(x, y, text(string, 10, position, color, vertical))
end;
function segment(x1, y1, x2, y2, color=:black; linestyle=:solid, linewidth=0.5)
plot!([x1, x2], [y1, y2], color=color, linestyle=linestyle, linewidth=linewidth)
end;
function draw(more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(x, y, r2, r3) = res[2]
println("(x, y, r2, r3) = $((x, y, r2, r3))")
plot()
circle(0, r3, r3, :green)
circle(r2, r2, r2, :red)
circle(-r2, r2, r2, :red)
circle(x, y, 2, :magenta)
circle(-x, y, 2, :magenta)
circle(0, 2, 2, :blue)
if more == true
segment(0, r3, x, y, :black)
point(0, 2, " 2", :blue)
point(0, r3, "r3 ", :green, :right)
point(r2, r2, "(r2,r2) ", :red, :right)
point(x, y, "(x,y)", :red, :top)
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;
(x, y, r2, r3) = (64/5, 22/5, 8, 14)