算額（その587）

算額（その587）

長崎市 鎮西大社諏訪神社 明治20年(1887)
米光丁: 長崎県の和算の概説
http://hyonemitsu.web.fc2.com/Nagasakiwasan.pdf

問題 1. 外円内に正三角形，大円，小円が入っている。大円，小円の直径が 60 寸，48 寸のとき，外円の直径はいかほどか。

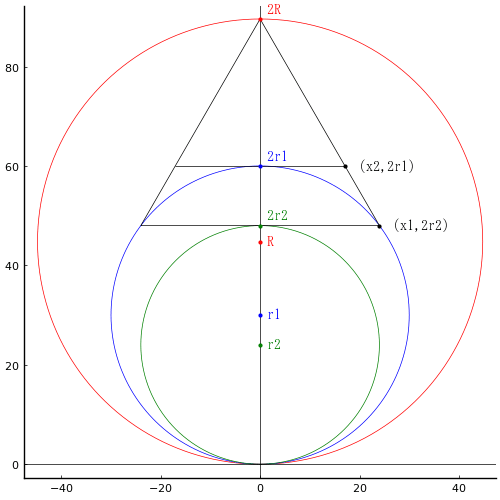
外円の半径と中心座標を R, (0, R)
大円の半径と中心座標を r1, (0, r1)
小円の半径と中心座標を r2, (0, r2)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms R::positive, r1::positive, r2::positive, x::positive

x = 2r2 - r1
eq = sqrt(r1^2 - x^2)/(2R - 2r2) - 1/sqrt(Sym(3))
res = solve(eq, R)
res |> println

   Sym[sqrt(3)*sqrt(r2)*sqrt(r1 - r2) + r2]

外円の半径は，sqrt(3)*sqrt(r2)*sqrt(r1 - r2) + r2 で求められる。
大円，中円の直径が 60 寸，48 寸のとき，外円の半径は 44.7846096908265 寸，直径は 89.5692193816530 寸である。

res[1](r1 => 60/2, r2 => 48/2).evalf() |> println
2res[1](r1 => 60/2, r2 => 48/2).evalf() |> println

   44.7846096908265
   89.5692193816530

算額の答えでは 89.568 寸としているが，外円の半径を小数点以下3桁まで求め（切り捨て）44.784 を 2 倍したのかもしれない。

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r2) = (60, 48) .// 2
   R = sqrt(3)*sqrt(r2)*sqrt(r1 - r2) + r2
   @printf("外円の直径 = %g;  R = %g; r1 = %g;  r2 = %g\n", 2R, R, r1, r2)
   plot()
   circle(0, R, R)
   circle(0, r1, r1, :blue)
   circle(0, r2, r2, :green)
   x1 = sqrt(r1^2 - (2r2 - r1)^2)
   plot!([-x1, x1, 0, -x1], [2r2, 2r2, 2R, 2r2], color=:black, lw=0.5)
   x2 = (2R - 2r1)/√3
   segment(-x2, 2r1, x2, 2r1, :black)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(0, 2R, " 2R", :red, :left, :bottom, delta=delta/2)
       point(0, 2r1, " 2r1", :blue, :left, :bottom, delta=delta/2)
       point(0, 2r2, " 2r2", :green, :left, :bottom, delta=delta/2)
       point(0, R, " R", :red, :left, :vcenter)
       point(0, r1, " r1", :blue, :left, :vcenter)
       point(0, r2, " r2", :green, :left, :vcenter)
       point(x1, 2r2, "  (x1,2r2)", :black, :left, :vcenter)
       point(x2, 2r1, "  (x2,2r1)", :black, :left, :vcenter)
   end
end;