算額（その2）

算額（その2）

問題2
群馬県高崎市 幸宮神社 文政7年(1824)
https://blog.goo.ne.jp/r-de-r/e/95e0d587bc8ce1d15512697ad8ad6102

下図のように大円，中円，小円がそれぞれ接しており，かつ x 軸にも接している。大円，中円，小円の半径にはどのような関係があるか。

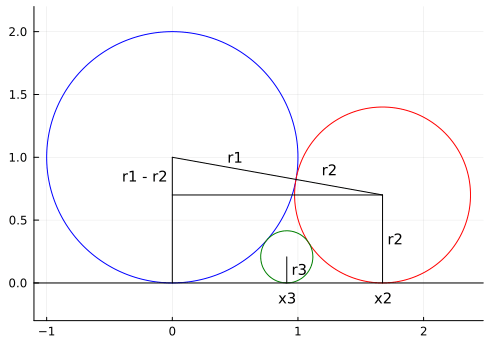
問題は半径　r1，r2，r3 だけを求めているが，図を描くために中円，小円の中心の x 座標 x2，x3 も求める。
なお，大円の中心を (0, r1) とする。

using SymPy

未知数は r1, r2, r3, x2, x3 の 5 個であるが，r1, r2 を与えれば残りの 3 変数が決まる。

@syms r1::positive, r2::positive, r3::positive, x2::positive, x3::positive

   (r1, r2, r3, x2, x3)

大円と中円が接することで，ピタゴラスの定理より，以下の方程式を得る。

eq1 = (r1 - r2)^2 + x2^2 - (r1 + r2)^2
eq1 |> println

   x2^2 + (r1 - r2)^2 - (r1 + r2)^2

x2 について解く。

solve(eq1, x2) |> println

   Sym[2*sqrt(r1)*sqrt(r2)]

中円と小円が接することで，同様にして以下の方程式を得る。

eq2 = (r2 - r3)^2 + (x2 - x3)^2 - (r2 + r3)^2
eq2 |> println

   (r2 - r3)^2 - (r2 + r3)^2 + (x2 - x3)^2

x2 は 2√r1√r2 とわかったので，置き換えて以下の方程式になる。

eq22 = eq2(x2 => 2√r1√r2)
eq22 |> println

   (r2 - r3)^2 - (r2 + r3)^2 + (2*sqrt(r1)*sqrt(r2) - x3)^2

大円と小円について同様に方程式を求める。

eq3 = (r1 - r3)^2 + x3^2 - (r1 + r3)^2
eq3 |> println

   x3^2 + (r1 - r3)^2 - (r1 + r3)^2

連立方程式 eq22, eq3 を x3, r3 について解く。

res = solve([eq22, eq3], (x3, r3));

解は二通り求まる。

3 番目の円が最も小さい場合 と 3 番目の円が最も大きい場合である。後者は，大円，中円，小円の定義から言うと不適切解であるが，一応両方の解を示しておく。

x3, r3 は，かなり長いが r1, r2 のみで表される。

- 第一の解の x3, r3

res[1][1] |> println # x3

   (r1*r2 + (r1 - r2)*(-2*r1^(3/2)*r2^(3/2)/(r1^2 - 2*r1*r2 + r2^2) + r1*r2*(r1 + r2)/(r1 - r2)^2))/(sqrt(r1)*sqrt(r2))

res[1][2] |> println # r3

   -2*r1^(3/2)*r2^(3/2)/(r1^2 - 2*r1*r2 + r2^2) + r1*r2*(r1 + r2)/(r1 - r2)^2

r3 は実は r1*r2/(sqrt(r1) + sqrt(r2))^2 であるが，SymPy では simplify できない。

- 第二の解の x3, r3

res[2][1] |> println # x3

   (r1*r2 + (r1 - r2)*(2*r1^(3/2)*r2^(3/2)/(r1^2 - 2*r1*r2 + r2^2) + r1*r2*(r1 + r2)/(r1 - r2)^2))/(sqrt(r1)*sqrt(r2))

res[2][2] |> println # r3

   2*r1^(3/2)*r2^(3/2)/(r1^2 - 2*r1*r2 + r2^2) + r1*r2*(r1 + r2)/(r1 - r2)^2

r3 は実は r1*r2/(sqrt(r1) - sqrt(r2))^2 であるが，SymPy では simplify できない。

図を描いて，正しいかどうか確かめる。

using Plots

function circle2(ox, oy, r; color=:red)
   theta = 0:0.01:2pi
   x = r.*cos.(theta)
   y = r.*sin.(theta)
   plot!(ox .+ x, oy .+ y, color=color)
end;

function draw(r1, r2)  # r1, r2 を与えれば図を描くことができる
   gr(size=(500, 500), aspectratio=1, label="")
   plot(ylims=(-0.2, 2.3))
   circle2(0, r1, r1, color=:blue)
   # x2 は r1 と r2 だけで決まる
   x2 = 2√r1√r2
   println("x2 = $x2")
   # 3 番目の円が最も小さい場合
   circle2(x2, r2, r2, color=:red)
   x3 = (r1*r2 + (r1 - r2)*(-2*r1^(3/2)*r2^(3/2)/(r1^2 - 2*r1*r2 + r2^2) + r1*r2*(r1 + r2)/(r1 - r2)^2))/(sqrt(r1)*sqrt(r2))
   r3 = -2*r1^(3/2)*r2^(3/2)/(r1^2 - 2*r1*r2 + r2^2) + r1*r2*(r1 + r2)/(r1 - r2)^2
   println("x3 = $x3, r3 = $r3")
   circle2(2√r3, r3, r3, color=:green)
   # 3 番目の円が最も大きい場合（r1 ≧ r2 ≧ r3 という条件をつけるなら，不適解になる）
   x3 = (r1*r2 + (r1 - r2)*(2*r1^(3/2)*r2^(3/2)/(r1^2 - 2*r1*r2 + r2^2) + r1*r2*(r1 + r2)/(r1 - r2)^2))/(sqrt(r1)*sqrt(r2))
   r3 =  2*r1^(3/2)*r2^(3/2)/(r1^2 - 2*r1*r2 + r2^2) + r1*r2*(r1 + r2)/(r1 - r2)^2
   println("x3 = $x3, r3 = $r3")
   circle2(2√r3, r3, r3, color=:brown)
   hline!([0], color=:black)
end;

draw(1, 0.26)

   x2 = 1.019803902718557
   x3 = 0.6754106793494012, r3 = 0.11404489644480492
   x3 = 2.0808160847548067, r3 = 1.0824488946435809