算額(その696)
神壁算法 關流神谷幸吉定令門人 本田帶刀家士 佐久間常右衛門久豊
藤田貞資(1789):神壁算法巻上
http://www.wasan.jp/jinpeki/jinpekisanpo1.pdf
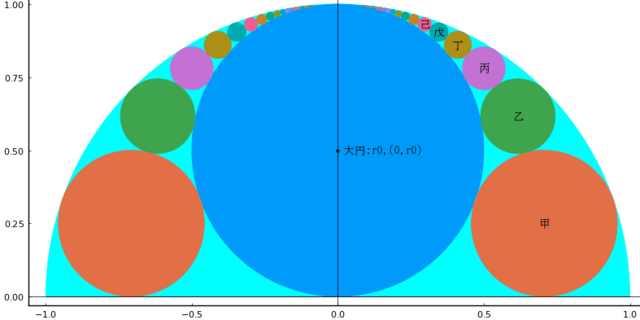
半円の中に大円および甲円から始まる累円が左右に位置している。大円の直径が与えられ,末円の径がわかったときに累円の個数はいくつあるか。
まず,累円の開始点として,甲円の半径と中心座標を求める。
大円の半径と中心座標を r0, (0, r0)
甲円の半径と中心座標を r1, (x1, y1); y1 = r1
include("julia-source.txt");
using SymPy
@syms r0::positive, r1::positive, x1::positive
eq1 = x1^2 + r1^2 - (2r0 - r1)^2
eq2 = x1^2 + (r0 - r1)^2 - (r0 + r1)^2
res2 = solve([eq1, eq2], (r1, x1))
1-element Vector{Tuple{Sym, Sym}}:
(r0/2, sqrt(2)*r0)
甲円の半径は大円の半径を r0 とすると r0/2,中心座標は (√2r0, r0/2) である。
甲円に外接する乙円のパラメータ(半径,中心座標)は,以下のようになる。
@syms y1::positive, r2::positive, x2::positive, y2::positive
eq3 = (x1 - x2)^2 + (y1 - y2)^2 - (r1 + r2)^2
eq4 = x2^2 + (r0 - y2)^2 - (r0 + r2)^2
eq5 = x2^2 + y2^2 - (2r0 - r2)^2
res3 = solve([eq3, eq4, eq5], (r2, x2, y2))
2-element Vector{Tuple{Sym, Sym, Sym}}:
((8*r0^3 + 4*r0^2*r1 - 20*r0^2*y1 - 2*r0*r1^2 - 4*r0*r1*y1 + 10*r0*x1^2 + 14*r0*y1^2 - r1^3 + 3*r1^2*y1 + r1*x1^2 + r1*y1^2 - 3*x1^2*y1 - 2*sqrt(2)*x1*sqrt(8*r0^3*r1 - 8*r0^3*y1 + 4*r0^2*r1^2 - 8*r0^2*r1*y1 + 4*r0^2*x1^2 + 4*r0^2*y1^2 - 2*r0*r1^3 - 2*r0*r1^2*y1 + 2*r0*r1*x1^2 + 2*r0*r1*y1^2 + 2*r0*x1^2*y1 + 2*r0*y1^3 - r1^4 + 2*r1^2*x1^2 + 2*r1^2*y1^2 - x1^4 - 2*x1^2*y1^2 - y1^4) - 3*y1^3)/(2*(4*r0^2 + 4*r0*r1 - 12*r0*y1 + r1^2 - 6*r1*y1 + 8*x1^2 + 9*y1^2)), (8*r0^2*x1 - 4*r0*r1*x1 - 4*r0*x1*y1 + 2*sqrt(2)*r0*sqrt(8*r0^3*r1 - 8*r0^3*y1 + 4*r0^2*r1^2 - 8*r0^2*r1*y1 + 4*r0^2*x1^2 + 4*r0^2*y1^2 - 2*r0*r1^3 - 2*r0*r1^2*y1 + 2*r0*r1*x1^2 + 2*r0*r1*y1^2 + 2*r0*x1^2*y1 + 2*r0*y1^3 - r1^4 + 2*r1^2*x1^2 + 2*r1^2*y1^2 - x1^4 - 2*x1^2*y1^2 - y1^4) - 4*r1^2*x1 + sqrt(2)*r1*sqrt(8*r0^3*r1 - 8*r0^3*y1 + 4*r0^2*r1^2 - 8*r0^2*r1*y1 + 4*r0^2*x1^2 + 4*r0^2*y1^2 - 2*r0*r1^3 - 2*r0*r1^2*y1 + 2*r0*r1*x1^2 + 2*r0*r1*y1^2 + 2*r0*x1^2*y1 + 2*r0*y1^3 - r1^4 + 2*r1^2*x1^2 + 2*r1^2*y1^2 - x1^4 - 2*x1^2*y1^2 - y1^4) + 4*x1^3 + 4*x1*y1^2 - 3*sqrt(2)*y1*sqrt(8*r0^3*r1 - 8*r0^3*y1 + 4*r0^2*r1^2 - 8*r0^2*r1*y1 + 4*r0^2*x1^2 + 4*r0^2*y1^2 - 2*r0*r1^3 - 2*r0*r1^2*y1 + 2*r0*r1*x1^2 + 2*r0*r1*y1^2 + 2*r0*x1^2*y1 + 2*r0*y1^3 - r1^4 + 2*r1^2*x1^2 + 2*r1^2*y1^2 - x1^4 - 2*x1^2*y1^2 - y1^4))/(4*r0^2 + 4*r0*r1 - 12*r0*y1 + r1^2 - 6*r1*y1 + 8*x1^2 + 9*y1^2), 3*sqrt(2)*x1*sqrt(-(-4*r0^2 - 4*r0*r1 - r1^2 + x1^2 + y1^2)*(2*r0*r1 - 2*r0*y1 - r1^2 + x1^2 + y1^2))/(4*r0^2 + 4*r0*r1 - 12*r0*y1 + r1^2 - 6*r1*y1 + 8*x1^2 + 9*y1^2) + (-8*r0^3 + 4*r0^2*r1 + 12*r0^2*y1 + 10*r0*r1^2 - 12*r0*r1*y1 + 2*r0*x1^2 - 6*r0*y1^2 + 3*r1^3 - 9*r1^2*y1 - 3*r1*x1^2 - 3*r1*y1^2 + 9*x1^2*y1 + 9*y1^3)/(2*(4*r0^2 + 4*r0*r1 - 12*r0*y1 + r1^2 - 6*r1*y1 + 8*x1^2 + 9*y1^2)))
((8*r0^3 + 4*r0^2*r1 - 20*r0^2*y1 - 2*r0*r1^2 - 4*r0*r1*y1 + 10*r0*x1^2 + 14*r0*y1^2 - r1^3 + 3*r1^2*y1 + r1*x1^2 + r1*y1^2 - 3*x1^2*y1 + 2*sqrt(2)*x1*sqrt(8*r0^3*r1 - 8*r0^3*y1 + 4*r0^2*r1^2 - 8*r0^2*r1*y1 + 4*r0^2*x1^2 + 4*r0^2*y1^2 - 2*r0*r1^3 - 2*r0*r1^2*y1 + 2*r0*r1*x1^2 + 2*r0*r1*y1^2 + 2*r0*x1^2*y1 + 2*r0*y1^3 - r1^4 + 2*r1^2*x1^2 + 2*r1^2*y1^2 - x1^4 - 2*x1^2*y1^2 - y1^4) - 3*y1^3)/(2*(4*r0^2 + 4*r0*r1 - 12*r0*y1 + r1^2 - 6*r1*y1 + 8*x1^2 + 9*y1^2)), (8*r0^2*x1 - 4*r0*r1*x1 - 4*r0*x1*y1 - 2*sqrt(2)*r0*sqrt(8*r0^3*r1 - 8*r0^3*y1 + 4*r0^2*r1^2 - 8*r0^2*r1*y1 + 4*r0^2*x1^2 + 4*r0^2*y1^2 - 2*r0*r1^3 - 2*r0*r1^2*y1 + 2*r0*r1*x1^2 + 2*r0*r1*y1^2 + 2*r0*x1^2*y1 + 2*r0*y1^3 - r1^4 + 2*r1^2*x1^2 + 2*r1^2*y1^2 - x1^4 - 2*x1^2*y1^2 - y1^4) - 4*r1^2*x1 - sqrt(2)*r1*sqrt(8*r0^3*r1 - 8*r0^3*y1 + 4*r0^2*r1^2 - 8*r0^2*r1*y1 + 4*r0^2*x1^2 + 4*r0^2*y1^2 - 2*r0*r1^3 - 2*r0*r1^2*y1 + 2*r0*r1*x1^2 + 2*r0*r1*y1^2 + 2*r0*x1^2*y1 + 2*r0*y1^3 - r1^4 + 2*r1^2*x1^2 + 2*r1^2*y1^2 - x1^4 - 2*x1^2*y1^2 - y1^4) + 4*x1^3 + 4*x1*y1^2 + 3*sqrt(2)*y1*sqrt(8*r0^3*r1 - 8*r0^3*y1 + 4*r0^2*r1^2 - 8*r0^2*r1*y1 + 4*r0^2*x1^2 + 4*r0^2*y1^2 - 2*r0*r1^3 - 2*r0*r1^2*y1 + 2*r0*r1*x1^2 + 2*r0*r1*y1^2 + 2*r0*x1^2*y1 + 2*r0*y1^3 - r1^4 + 2*r1^2*x1^2 + 2*r1^2*y1^2 - x1^4 - 2*x1^2*y1^2 - y1^4))/(4*r0^2 + 4*r0*r1 - 12*r0*y1 + r1^2 - 6*r1*y1 + 8*x1^2 + 9*y1^2), -3*sqrt(2)*x1*sqrt(-(-4*r0^2 - 4*r0*r1 - r1^2 + x1^2 + y1^2)*(2*r0*r1 - 2*r0*y1 - r1^2 + x1^2 + y1^2))/(4*r0^2 + 4*r0*r1 - 12*r0*y1 + r1^2 - 6*r1*y1 + 8*x1^2 + 9*y1^2) + (-8*r0^3 + 4*r0^2*r1 + 12*r0^2*y1 + 10*r0*r1^2 - 12*r0*r1*y1 + 2*r0*x1^2 - 6*r0*y1^2 + 3*r1^3 - 9*r1^2*y1 - 3*r1*x1^2 - 3*r1*y1^2 + 9*x1^2*y1 + 9*y1^3)/(2*(4*r0^2 + 4*r0*r1 - 12*r0*y1 + r1^2 - 6*r1*y1 + 8*x1^2 + 9*y1^2)))
2 組の解が得られるが,最初のものが適解である。
乙円の半径はかなり長い式になり,これ以上簡約化もできないが,この式は,「一つ前の累円のパラメータから,それに外接する累円のパラメータを得る」漸化式である。
これを関数にすると,以下のようになる。
現在の累円の半径,中心座標を与えると,次の累円の半径,中心座標を返す。
nextcircle(r0, r1, x1, y1) = ((8*r0^3 + 4*r0^2*r1 - 20*r0^2*y1 - 2*r0*r1^2 - 4*r0*r1*y1 + 10*r0*x1^2 + 14*r0*y1^2 - r1^3 + 3*r1^2*y1 + r1*x1^2 + r1*y1^2 - 3*x1^2*y1 - 2*sqrt(2)*x1*sqrt(8*r0^3*r1 - 8*r0^3*y1 + 4*r0^2*r1^2 - 8*r0^2*r1*y1 + 4*r0^2*x1^2 + 4*r0^2*y1^2 - 2*r0*r1^3 - 2*r0*r1^2*y1 + 2*r0*r1*x1^2 + 2*r0*r1*y1^2 + 2*r0*x1^2*y1 + 2*r0*y1^3 - r1^4 + 2*r1^2*x1^2 + 2*r1^2*y1^2 - x1^4 - 2*x1^2*y1^2 - y1^4) - 3*y1^3)/(2*(4*r0^2 + 4*r0*r1 - 12*r0*y1 + r1^2 - 6*r1*y1 + 8*x1^2 + 9*y1^2)), (8*r0^2*x1 - 4*r0*r1*x1 - 4*r0*x1*y1 + 2*sqrt(2)*r0*sqrt(8*r0^3*r1 - 8*r0^3*y1 + 4*r0^2*r1^2 - 8*r0^2*r1*y1 + 4*r0^2*x1^2 + 4*r0^2*y1^2 - 2*r0*r1^3 - 2*r0*r1^2*y1 + 2*r0*r1*x1^2 + 2*r0*r1*y1^2 + 2*r0*x1^2*y1 + 2*r0*y1^3 - r1^4 + 2*r1^2*x1^2 + 2*r1^2*y1^2 - x1^4 - 2*x1^2*y1^2 - y1^4) - 4*r1^2*x1 + sqrt(2)*r1*sqrt(8*r0^3*r1 - 8*r0^3*y1 + 4*r0^2*r1^2 - 8*r0^2*r1*y1 + 4*r0^2*x1^2 + 4*r0^2*y1^2 - 2*r0*r1^3 - 2*r0*r1^2*y1 + 2*r0*r1*x1^2 + 2*r0*r1*y1^2 + 2*r0*x1^2*y1 + 2*r0*y1^3 - r1^4 + 2*r1^2*x1^2 + 2*r1^2*y1^2 - x1^4 - 2*x1^2*y1^2 - y1^4) + 4*x1^3 + 4*x1*y1^2 - 3*sqrt(2)*y1*sqrt(8*r0^3*r1 - 8*r0^3*y1 + 4*r0^2*r1^2 - 8*r0^2*r1*y1 + 4*r0^2*x1^2 + 4*r0^2*y1^2 - 2*r0*r1^3 - 2*r0*r1^2*y1 + 2*r0*r1*x1^2 + 2*r0*r1*y1^2 + 2*r0*x1^2*y1 + 2*r0*y1^3 - r1^4 + 2*r1^2*x1^2 + 2*r1^2*y1^2 - x1^4 - 2*x1^2*y1^2 - y1^4))/(4*r0^2 + 4*r0*r1 - 12*r0*y1 + r1^2 - 6*r1*y1 + 8*x1^2 + 9*y1^2), 3*sqrt(2)*x1*sqrt(-(-4*r0^2 - 4*r0*r1 - r1^2 + x1^2 + y1^2)*(2*r0*r1 - 2*r0*y1 - r1^2 + x1^2 + y1^2))/(4*r0^2 + 4*r0*r1 - 12*r0*y1 + r1^2 - 6*r1*y1 + 8*x1^2 + 9*y1^2) + (-8*r0^3 + 4*r0^2*r1 + 12*r0^2*y1 + 10*r0*r1^2 - 12*r0*r1*y1 + 2*r0*x1^2 - 6*r0*y1^2 + 3*r1^3 - 9*r1^2*y1 - 3*r1*x1^2 - 3*r1*y1^2 + 9*x1^2*y1 + 9*y1^3)/(2*(4*r0^2 + 4*r0*r1 - 12*r0*y1 + r1^2 - 6*r1*y1 + 8*x1^2 + 9*y1^2)));
nextcircle(0.5, 0.25, 0.7071067811865476, 0.25)
(0.12773958089728293, 0.6167812573081513, 0.6167812573081511)
nextcircle(0.5, 0.12773958089728296, 0.6167812573081511, 0.6167812573081513)
(0.07322330470336305, 0.4999999999999999, 0.7803300858899107)
この関数を用いて,甲円を初期値として,乙円,丙円のパラメータを求める。
各行の後半 4 項目,r0/rn, f(n), n については後に説明する。
r0 = 1/2
r, x, y = nextcircle(r0, r0/2, sqrt(2)*r0, r0/2) # 2
for i = 2:10
println(i, ",", r, ",", x, ",", y, ", r0/rn = ", r0/r, ", f(n) = ", 0.5*i^2 + 0.414213562374*i + 1.08578643763, ", n = ", round(Int, sqrt(2*r0/r - 2) - sqrt(2) + 1))
r, x, y = nextcircle(r0, r, x, y)
end
2,0.12773958089728293,0.6167812573081513,0.6167812573081511, r0/rn = 3.914213562373095, f(n) = 3.914213562378, n = 2
3,0.07322330470336313,0.5,0.7803300858899105, r0/rn = 6.828427124746189, f(n) = 6.828427124752, n = 3
4,0.04654349098723124,0.41090581831205225,0.8603695270383063, r0/rn = 10.742640687119284, f(n) = 10.742640687126, n = 4
5,0.03193489522432071,0.34580468567296235,0.9041953143270376, r0/rn = 15.65685424949239, f(n) = 15.6568542495, n = 5
6,0.023179195594803567,0.2973526214981749,0.9304624132155892, r0/rn = 21.571067811865422, f(n) = 21.571067811874, n = 6
7,0.017552924734392517,0.26028226525009357,0.9473412257968229, r0/rn = 28.48528137423842, f(n) = 28.485281374247997, n = 7
8,0.013736454334619978,0.23116292072255745,0.95879063699614, r0/rn = 36.399494936611866, f(n) = 36.399494936622, n = 8
9,0.011034188473256403,0.20775641354942292,0.9668974345802309, r0/rn = 45.31370849898491, f(n) = 45.313708498996, n = 9
10,0.009053391497230267,0.18856790503185952,0.9728398255083086, r0/rn = 55.22792206135862, f(n) = 55.22792206137, n = 10
甲円を1番目として,n 番目の累円の半径を rn として,r0/rn を n の多項式で表すことを考える。
多項式回帰分析により,r0/rn = f(n) = 0.5*n^2 + 0.414213562374*n + 1.08578643763 が得られる。
この多項式の逆関数を得れば,r0/rn から n を求めることができる。
逆関数は以下のようになる。
@syms n, r0_by_rn
eq = 0.5*n^2 + 0.414213562374*n + 1.08578643763 - r0_by_rn
solve(eq, n)[2] |> println
1.41421356237502*sqrt(0.99999999999728*r0_by_rn - 1) - 0.414213562374
1.41421356237502 は √2, 0.99999999999728 は 1, 0.414213562374 は √2 - 1 なので,以下のように書ける。
sqrt(Sym(2))*sqrt(r0_by_rn - 1) + 1 - sqrt(Sym(2))|> simplify |> println
sqrt(2*r0_by_rn - 2) - sqrt(2) + 1
何番目の累円かを知るには,「大円の半径を n 番目の累円の半径で割ったものを 2 倍して,2 を引いて,平方根を求め,1 を加えて,2 の平方根を引く」
これを関数にすると以下のようになる。累円の半径を与えるとそれが何番目のものかを返す。
nth(rn) = round(Int, sqrt(2r0/rn - 2) + 1 - sqrt(2));
たとえば,10 番目の累円の半径は上の実行結果から,0.009053391497230267 なので,何番目かは nth(0.009053391497230267) = 10 になる。
nth(0.009053391497230267)
10
function draw(more=false)
pyplot(size=(800, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
names = Char["甲乙丙丁戊己庚辛壬癸"...]
s2 = sqrt(2)
plot()
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
r0 = 1/2
circlef(0, 0, 2r0, :cyan, beginangle=0, endangle=180)
segment(-2r0, 0, 2r0, 0)
circlef(0, r0, r0, 1)
(r1, x1, y1) = (r0/2, sqrt(2)*r0, r0/2)
for i in 2:25
circlef(x1, y1, r1, i)
circlef(-x1, y1, r1, i)
i < 8 && point(x1, y1, names[i - 1], :black, :center, :vcenter, mark=false)
(r1, x1, y1) = nextcircle(r0, r1, x1, y1)
end
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
point(0, r0, " 大円:r0,(0,r0)", :black, :left, :vcenter)
end
end;



















