算額（その680）

算額（その680）

長野県信州新町日名 日置神社 明治44年(1911)
中村信弥「改訂増補 長野県の算額」県内の算額(270)
http://www.wasan.jp/zoho/zoho.html

第7問　正方形内に大円と小円がある正方形の面積が 235平方寸，外積（正方形と二円の間の面積）が 132.45平方寸，大小の円の直径の差が 2 寸のとき，小円の直径を求めよ。ただし円積率を 0.7 とする（円周率を 4*0.7 とするということ）。

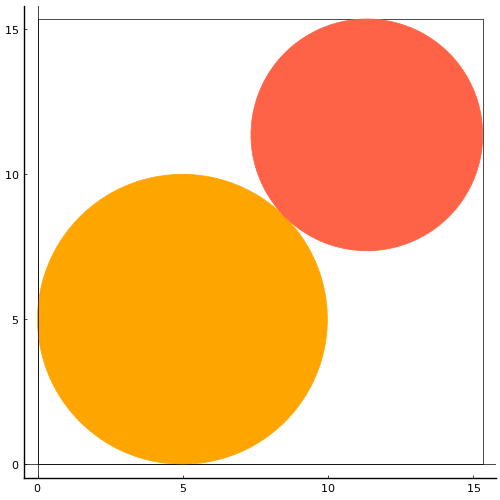
正方形の一辺の長さを a, 二円の半径を r1, r2 とし，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms r1::positive, r2::positive, 円周率::positive,
     a::positive
円周率 = 4 * 0.7
a = √235
eq2 = a^2 - 円周率*(r1^2 + r2^2) - 132.45
eq3 = 2r1 - 2r2 - 2;
res = solve([eq2, eq3], (r1, r2))

   1-element Vector{Tuple{Sym, Sym}}:
    (4.75000000000000, 3.75000000000000)

小円の直径は 2*3.75 = 7.5 寸である。
この設定で図を描いても，2 つの円は外接しない。

---

円周率として π を使い，正方形内の2円が外接するとして，外積がいくつになるか計算してみる。

using SymPy
@syms r1::positive, r2::positive, 円周率::positive,
     a::positive
円周率 = PI
a = √Sym(235)
eq2 = √Sym(2)*(a - r2 - r1) - (r1 + r2) 
eq3 = 2r1 - 2r2 - 2;
res = solve([eq2, eq3], (r1, r2))

   Dict{Any, Any} with 2 entries:
     r2 => -sqrt(470)/2 - 1/2 + sqrt(235)
     r1 => -sqrt(470)/2 + 1/2 + sqrt(235)

r1 = -sqrt(470)/2 + 1/2 + sqrt(235)
r2 = -sqrt(470)/2 - 1/2 + sqrt(235)
外積 = (a^2 - 円周率*(r1^2 + r2^2))
(r1, r2, 外積.evalf())

   (4.989968022416491, 3.989968022416491, 106.761363826833)

外積はほぼ 106.76 である。この結果だと，ちゃんと二円は外接する。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (a, r1, r2) = (√235, -sqrt(470)/2 + 1/2 + sqrt(235), -sqrt(470)/2 - 1/2 + sqrt(235))
   @printf("a = %g;  r1 = %g;  r2 = %g\n", a, r1, r2)
   plot([0, a, a, 0, 0], [0, 0, a, a, 0], color=:black, lw=0.5)
   circlef(r1, r1, r1, :orange)
   circlef(a - r2, a - r2, r2, :tomato)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
   end
end;

算額（その679）

算額（その679）

長野県飯山市下木島 鳥出神社 天保14年(1843)
中村信弥「改訂増補 長野県の算額」県内の算額（166）
http://www.wasan.jp/zoho/zoho.html

三角形内に三辺に接する全円と，中鈎（頂点から底辺への垂線）と二辺に接する中円と小円が入っている。全円，中円，小円の直径がそれぞれ 7寸，6寸，4寸のとき，中鈎の長さ（三角形の高さ）はいかほどか。

中鈎と底辺の交点を原点と定め，右の頂点と左の頂点の座標を (a, 0), (-b, 0)，高さを h とする。
全円の半径と中心座標を r1, (x1, r1)
中円の半径と中心座標を r2, (r2, r2)
小円の半径と中心座標を r3, (-r3, r3)
とおき，以下の連立方程式を解く。
4 元連立方程式として解くと不適切な解になるので，eq1, eq2, eq3 から a, b, h を求め，そのあと eq4 から x1 を求める。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms a::positive, b::negative, h::positive,
     r1::positive, x1::positive,
     r2::positive, r3::positive, l1::positive, l2::positive
(r1, r2, r3) = (7, 6, 4) .// 2
l1 = sqrt(a^2 + h^2)
l2 = sqrt(b^2 + h^2)
eq1 = (a - b + l1 + l2)*r1 - (a - b)*h
eq2 = a + h - l1 - 2r2
eq3 = -b + h - l2 - 2r3;
res1 = solve([eq1, eq2, eq3], (a, b, h))

   1-element Vector{Tuple{Sym, Sym, Sym}}:
    (15, -6, 8)

中鈎の長さ（三角形の高さ）は 8 寸である。

@syms a::positive, b::negative, h::positive,
     r1::positive, x1::positive, y1::positive,
     r2::positive, r3::positive, l1::positive, l2::positive
(r1, r2, r3) = (7, 6, 4) .// 2
(a, b, h) = (15, -6, 8)
eq4 = dist(a, 0, 0, h, x1, r1) - r1^2
res2 = solve(eq4, x1)
res2 |> println

   Sym[0.999999999999994, 15.8750000000000]

x1 = 1 が適解である。

その他のパラメータは以下の通りである。

   r1 = 3.5;  r2 = 3;  r3 = 2;  a = 15;  b = -6;  h = 8;  x1 = 1

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r2, r3) = (7, 6, 4) .// 2
   (a, b, h) = res1[1]
   x1 = res2[1]
   @printf("r1 = %g;  r2 = %g;  r3 = %g;  a = %g;  b = %g;  h = %g;  x1 = %g\n",
       r1, r2, r3, a, b, h, x1)
   plot([a, 0, b, a], [0, h, 0, 0], color=:black, lw=0.5)
   circle(x1, r1, r1)
   circle(r2, r2, r2, :blue)
   circle(-r3, r3, r3, :green)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(a, 0, " a", :black, :left, :bottom, delta=delta)
       point(b, 0, "b", :black, :right, :bottom, delta=delta)
       point(0, h, " h", :black, :left, :bottom, delta=delta)
       point(x1, r1, "    全円:r1\n    (x1,r1)", :red, :center, :bottom, delta=delta)
       point(r2, r2, "中円:r2\n(r2,r2)", :blue, :center, :top, delta=-delta)
       point(-r3, r3, "小円:r3\n(-r3,r3)", :green, :center, :top, delta=-delta)
   end
end;

 

算額（その678）

算額（その678）

長野県小諸市諸 金毘羅社 文政7年(1824)
中村信弥「改訂増補 長野県の算額」県内の算額（106）
http://www.wasan.jp/zoho/zoho.html

円内に等楕円が 3 個入っている。円の直径が 99 寸のとき，楕円の面積が最大になるときの楕円の長径を求めよ。

円の半径と中心座標を R, (0, 0)
楕円の長径，短径と中心座標を a, b, (0, y)
円と楕円の共通接点を (x1, y1)
上と右の楕円の共通接点を (x2, y2)
とおき，以下の連立方程式を解く。

eq1, eq2, eq3 は円と楕円が共通接点 (x1, y1) を持つこと，
eq4, eq5 は 2 つの楕円が共通接点 (x2, y2) を持つことを意味している。
これらの方程式群から，楕円の中心の y 座標を求める。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms x1::positive, y1::positive, x2::positive, y2::positive, y::positive, a::positive, b::positive, R::positive
y2 = x2/sqrt(Sym(3))
eq1 = x1^2/a^2 + (y1 - y)^2/b^2 - 1
eq2 = b^2*x1/(a^2*(y - y1)) + x1/y1
eq3 = x1^2 + y1^2 - R^2
eq4 = x2^2/a^2 + (y2 - y)^2/b^2 - 1
eq5 = b^2*x2/(a^2*(y - y2))- 1/sqrt(Sym(3));

res1 = solve([eq1, eq2, eq3], (x1, y1, y))

   2-element Vector{Tuple{Sym, Sym, Sym}}:
    (sqrt((-R^2*b^2 + a^4)/(a - b))/sqrt(a + b), a*sqrt(R^2*a^2 - R^2*b^2 - a^4 + a^2*b^2)/(a^2 - b^2), sqrt(R^2*a^2 - R^2*b^2 - a^4 + a^2*b^2)/a)
    (-sqrt(-(R^2*b^2 - a^4)/(a - b))/sqrt(a + b), a*sqrt(R^2*a^2 - R^2*b^2 - a^4 + a^2*b^2)/(a^2 - b^2), sqrt(R^2*a^2 - R^2*b^2 - a^4 + a^2*b^2)/a)

res2 = solve([eq4, eq5], (x2, y))

   1-element Vector{Tuple{Sym, Sym}}:
    (a^2/sqrt(a^2 + 3*b^2), sqrt(3*a^2 + 9*b^2)/3)

両方の解 y が等しいとすると以下のようになる。

eq = res1[1][3] - res2[1][2]
eq |> println

   -sqrt(3*a^2 + 9*b^2)/3 + sqrt(R^2*a^2 - R^2*b^2 - a^4 + a^2*b^2)/a

方程式を b について解く。

res3 = solve(eq,  b)
res3[1] |> println

   a*sqrt(9*R^2 - 12*a^2)/(3*R)

楕円の面積 S は長軸の長さ a の関数になり，以下のような外形である。

S = PI * a * a*sqrt(9*R^2 - 12*a^2)/(3*R);

円の半径を R = 99/2 として，図を描いてみる。
a が 30〜40 の間で面積が最大になることがわかる。

pyplot(size=(300, 200), grid=false, aspectratio=:none, label="", fontfamily="IPAMincho")
plot(S(R => 99/2), xlims=(0, 43), xlabel="長径 a", ylabel="楕円の面積 S")

S の導関数を求め，接線の傾きが 0 になるときの a を求める。

max_at_a = solve(diff(S, a), a)
max_at_a[1] |> println

   sqrt(2)*R/2

a の値が 35.0017856687341 のとき，面積が最大値 8888.52378442978 になる。

max_at_a[1](R => 99/2).evalf() |> println

   35.0017856687341

S(R => 99/2, a => 35.0017856687341).evalf() |> println

   2222.13094610745

そのときの短径 b は 20.2082903779612 である。

(a*sqrt(9*R^2 - 12*a^2)/(3*R))(R => 99/2, a => 35.0017856687341).evalf() |> println

   20.2082903779612

算額において，長径，短径は差渡し径なので，現代の用語で表すものの 2 倍である。
よって，算額の答えとしては「長径は 70.0035713374682，短径は 40.4165807559224」である。

その他のパラメータは以下の通り。

   x1 = 24.75;  y1 = 42.8683;  x2 = 24.75; y2 = 14.2894;  y = 28.5788;  a = 35.0018;  b = 20.2083

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   R = 99/2
   a = √2R/2
   b = a*sqrt(9*R^2 - 12*a^2)/(3*R)
   (x1, y1, y) = (sqrt((-R^2*b^2 + a^4)/(a - b))/sqrt(a + b),
       a*sqrt(R^2*a^2 - R^2*b^2 - a^4 + a^2*b^2)/(a^2 - b^2),
       sqrt(R^2*a^2 - R^2*b^2 - a^4 + a^2*b^2)/a)
   x2 = a^2/sqrt(a^2 + 3*b^2)
   y2 = x2/sqrt(3)
   @printf("x1 = %g;  y1 = %g;  x2 = %g; y2 = %g;  y = %g;  a = %g;  b = %g\n", x1, y1, x2, y2, y, a, b)
   plot()
   circle(0, 0, R)
   ellipse(0, y, a, b, color=:blue)
   ellipse(√3y/2, -y/2, a, b, φ=240, color=:blue)
   ellipse(-√3y/2, -y/2, a, b, φ=300, color=:blue)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(x1, y1, " (x1,y1)", :blue, :left, :bottom)
       point(x2, y2, " (x2,y2)", :blue, :left)
       point(0, y, " y", :blue, :left, :vcenter)
   end
end;