算額(その306)
「三重県に現存する算額の研究」福島完(2007/2/13)
https://mie-u.repo.nii.ac.jp/?action=repository_uri&item_id=7216
三重県伊賀市 永保寺 天保15年(1844)
問題文2
三辺のの和が 26.14 丈となる鉤股弦(直角三角形)がある。鉤股の差は分からないが,弦は鉤より 4.44 丈長い。この直角三角形に内接するように正三角形を入れるとき,正三角形の一辺,中句,三角面を求めよ。
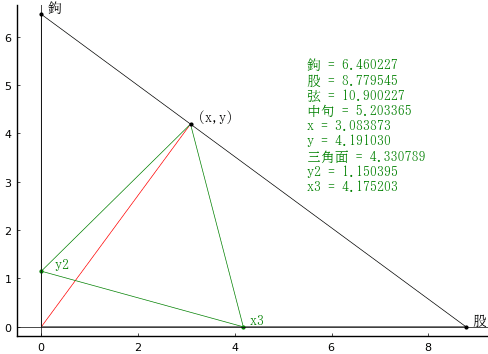
中句と弦の交点を (x, y),正三角形の他の 2 点を (x, y2), (x3, 0) とおき,以下の連立方程式を解く。
まず,鉤, 股, 弦, 中句 を求める。
include("julia-source.txt");
using SymPy
@syms 鉤::positive, 股::positive, 弦::positive,
中句::positive, 三角面::positive;
eq1 = 弦 - 鉤 - 4.44
eq2 = 鉤 + 股 + 弦 - 26.14
eq3 = 鉤^2 + 股^2 - 弦^2
eq4 = 中句 * 弦 - 鉤 * 股 # 鉤股弦の面積算出法が2通りある
solve([eq1, eq2, eq3, eq4], (鉤, 股, 弦, 中句))
1-element Vector{NTuple{4, Sym}}:
(6.46022727742318, 8.77954544515363, 10.9002272774232, 5.20336480374436)
正確な数値はともかく,出題文を勘案すれば小数点以下3桁目で四捨五入すべきであろう。
(鉤, 股, 弦) = (6.46, 8.78, 10.90)
鉤 + 股 + 弦 |> println
弦 - 鉤 |> println
sqrt(6.46^2 + 8.78^2) |> println
26.14
4.44
10.900458705944443
(鉤, 股, 弦, 中句) = (6.46, 8.78, 10.90, 5.20) とするのが妥当。
ちなみに,算額の「答」は記述間違い(6.46 を 6.64 とするなど),計算自体の間違い(弦を 11.1 とするなど)があり信頼性がない。
なお,以上の解法では図を描くことはできない(中句の長さだけでは図を描けない)ので,以下のような別解を探る。
まず,鉤,股,弦,中句の他に中句と弦の交点座標 (x, y) を求める。
using SymPy
@syms 鉤::positive, 股::positive, 弦::positive,
中句::positive, x::positive, y::positive;
eq1 = 弦 - 鉤 - 4.44
eq2 = 鉤 + 股 + 弦 - 26.14
eq3 = 鉤^2 + 股^2 - 弦^2
eq4 = 中句 * 弦 - 鉤 * 股 # 鉤股弦の面積算出法が2通りある
eq5 = y - (股 - x)*鉤/股
eq6 = x^2 + y^2 - 中句^2
res = solve([eq1, eq2, eq3, eq4, eq5, eq6], (鉤, 股, 弦, x, y, 中句))
1-element Vector{NTuple{6, Sym}}:
(6.46022727742318, 8.77954544515363, 10.9002272774232, 3.08387324263936, 4.19102983813985, 5.20336480374436)
弦の上にある (x, y) を頂点の一つとして,鉤,股の上に他の2つの頂点 (0, y2),(x3, 0) がある正三角形の x3, y2 を求めるが,上述の eq1〜eq6 に2条件を加えて一挙に8元連立方程式を解くのは solve() では無理なので,
(鉤, 股, 弦, x, y, 中句) = (6.46022727742318, 8.77954544515363, 10.9002272774232, 3.08387324263936, 4.19102983813985, 5.20336480374436) が既知であるとして,以下の二元連立方程式を解く。
@syms x3::positive, y2::positive
(鉤, 股, 弦, x, y, 中句) = (6.46022727742318, 8.77954544515363, 10.9002272774232, 3.08387324263936, 4.19102983813985, 5.20336480374436)
eq7 = (x^2 + (y - y2)^2) - (x3^2 + y2^2)
eq8 = ((x - x3)^2 + y^2) - (x3^2 + y2^2)
res = solve([eq7, eq8], (x3, y2))
1-element Vector{Tuple{Sym, Sym}}:
(4.17520337305602, 1.15039530221371)
算額の三角面の答えは 3.939986... とあり,「三重県に現存する算額の研究」福島完では 3.809101139 と不一致を見せている。しかし,後者も現代的解法の 60 ページに,BD = DG + GB = √3/2 DF + 1/2 DF としているところがあるが,GB は DF/2 ではない。掲載している図も実際の位置関係を表すものではない。GB = GF としているがそれは成り立たない。他の算額も同じであるが,図を描くための全てのパラメータを求めて,実際に図を描いてみれば,得られたパラメータが妥当なものかどうか明らかになる。想定していた図と全く異なる図になることもすぐに分かるはず。三角面が 3.809101139 の正三角形は描けない。
鉤 = 6.460227
股 = 8.779545
弦 = 10.900227
中句 = 5.203365
x = 3.083873
y = 4.191030
三角面 = 4.330789
y2 = 1.150395
x3 = 4.175203
using Plots
function draw(zoomin=false, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(鉤, 股, 弦, x, y, 中句) = (6.46022727742318, 8.77954544515363,
10.9002272774232, 3.08387324263936, 4.19102983813985,
5.20336480374436)
(x3, y2) = (4.17520337305602, 1.15039530221371)
三角面 = sqrt(x3^2 + y2^2)
txt = @sprintf("鉤 = %.6f\n", 鉤) * @sprintf("股 = %.6f\n", 股) *
@sprintf("弦 = %.6f\n", 弦) * @sprintf("中句 = %.6f\n", 中句) *
@sprintf("x = %.6f\n", x) * @sprintf("y = %.6f\n", y) *
@sprintf("三角面 = %.6f\n", 三角面) * @sprintf("y2 = %.6f\n", y2) *
@sprintf("x3 = %.6f\n", x3)
println(txt)
plot([0, 0, 股, 0], [0, 鉤, 0, 0], color=:black, lw=0.5)
segment(0, 0, x, y, :red)
plot!([x, 0, x3, x], [y, y2, 0, y], color=:green, lw=0.5)
if more
point(0, 鉤, " 鉤", :black, :left, :bottom)
point(股, 0, " 股", :black, :left, :bottom)
point(x, y, " (x,y)", :black, :left, :bottom)
point(0, y2, " y2", :green, :left, :bottom)
point(x3, 0, " x3", :green, :left, :bottom)
annotate!(5.5, 4.0, text(txt, :left, :green, 10))
vline!([0], color=:black, lw=0.5)
hline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;


















