算額（その293）

算額（その293）

中村信弥「算額への招待 追補1」
http://www.wasan.jp/syotai/syotai.html
長野県飯山市滝澤家所蔵
http://www.wasan.jp/nagano/takizawa.html

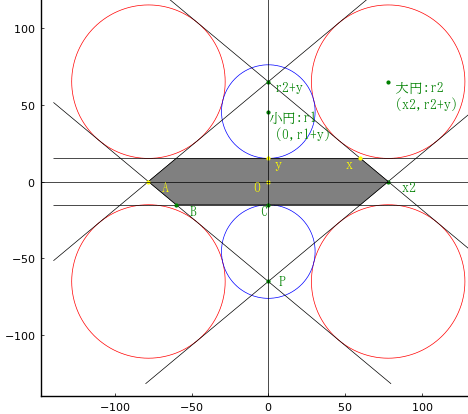
長方形内に 3 個の円が内接している。円の直径が 5 寸のとき，長方形の短辺の長さを求めよ。

問では3個の円について述べており，右上，左上の2個の円についての記述はない。意図は良くわからないがここではこの円についても半径を求めておく。

長方形の短辺の長さを y とする。
半径，中心座標を以下のように決める。
円　 r1, (r1, r1), (0, y - r1)
小円 r2, (r2, y - r2)

以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms r1::positive, r2::positive, y::positive;

eq1 = r1^2 + (y - 2r1)^2 - 4r1^2
eq2 = (2r1 - r2)^2 + (r1 - r2)^2 - (r1 + r2)^2
res = solve(eq1, y)
res |> println

   Sym[r1*(2 - sqrt(3)), r1*(sqrt(3) + 2)]

解が 2 つ求まるが，r1*(sqrt(3) + 2) が適解である。
すなわち短辺の長さは 5/2 * (sqrt(3) + 2) = 9.330127018922193 寸である。

5/2 * (sqrt(3) + 2)

   9.330127018922193

res2 = solve([eq1, eq2], (y, r2))

   4-element Vector{Tuple{Sym, Sym}}:
    (r1*(2 - sqrt(3)), 2*r1*(2 - sqrt(3)))
    (r1*(2 - sqrt(3)), 2*r1*(sqrt(3) + 2))
    (r1*(sqrt(3) + 2), 2*r1*(2 - sqrt(3)))
    (r1*(sqrt(3) + 2), 2*r1*(sqrt(3) + 2))

三番目の組が適解である。

   y = 9.33013;  r2 = 1.33975

小円の半径は 2*r1*(2 - sqrt(3)) = 1.33975 である。

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 5 / 2
   (y, r2) = (r1*(sqrt(3) + 2), 2*r1*(2 - sqrt(3)))
   @printf("y = %.5f;  r2 = %.5f\n", y, r2)
   plot([0, 4r1, 4r1, 0, 0], [0, 0, y, y, 0], color=:black, lw=0.5)
   circle(r1, r1, r1)
   circle(3r1, r1, r1)
   circle(2r1, y - r1, r1)
   circle(r2, y - r2, r2, :blue)
   circle(4r1 - r2, y - r2, r2, :blue)
   if more
       point(r1, r1, "(r1,r1)", :red)
       point(3r1, r1, "(3r1,r1)", :red)
       point(2r1, y - r1, "(0,y-r1)", :red)
       point(r2, y - r2, "(r2,y-r2)", :blue, :center)
       point(4r1-r2, y - r2, "(4r1-r2,y-r2)", :blue, :center)
       point(0, y, " y")
       point(4r1, 0, "4r1 ", :green, :right, :bottom)
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

 

算額（その292）

算額（その292）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額(282)
長野県中野市片塩 大徳寺 天保9年(1838)

大円と小円は互いに外接し，また 2 本の平行線の上下に接している。斜線は大円の共通接線である。
大円と小円の直径がそれぞれ 100 寸，61 寸のとき，黒く塗られた部分の面積（歩）を求めよ。

原点と平行線の距離を y とする。
小円の半径と中心座標 r1, (0, r1 + y)
大円の半径と中心座標 r2, (x2, r2 + y)
共通接線の傾きは ±((r2 + y) / x2)，共通接線と平行線の交点の x 座標は ±x である。

include("julia-source.txt");

using SymPy

@syms r1::positive, r2::positive, x2::positive, y::positive;

(r1, r2) = (61//2, 100//2)
eq1 = x2^2 + (r2 - r1)^2 - (r2 + r1)^2
eq2 = distance(0, r2 + y, x2, 0, x2, r2 + y) - r2^2
res = solve([eq1, eq2], (x2, y))

   1-element Vector{Tuple{Sym, Sym}}:
    (10*sqrt(61), -50 + 25*sqrt(61)/3)

   x2 = 78.10250;  y = 15.08541
   黒い部分の面積 = 4166.666666666663

黒の部分の面積は，⊿PAO - ⊿PBC = 2((r2 + y)\*x2 - r2\*x) = 4166.666666666663 = 4166+2/3 である。

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r2) = (61//2, 100//2)
   (x2, y) = (10*sqrt(61), -50 + 25*sqrt(61)/3)
   @printf("x2 = %.5f;  y = %.5f\n", x2, y)
   plot()
   circle4(x2, r2 + y, r2)
   circle(0, r1 + y, r1, :blue)
   circle(0, -r1 - y, r1, :blue)
   slope = (r2 + y) / x2
   abline(x2, r2 + y, slope, -140, 80, :black)
   abline(x2, r2 + y, -slope, -80, 140, :black)
   abline(-x2, -r2 - y, slope, -80, 140, :black)
   abline(-x2, -r2 - y, -slope, -140, 80, :black)
   segment(-140, y, 140, y, :black)
   segment(-140, -y, 140, -y, :black)
   if more
       point(x2, 0, "  x2")
       point(0, r2 + y, " r2+y")
       point(x2, r2 + y, " 大円:r2\n (x2,r2+y)")
       point(0, r1 + y, "小円:r1\n (0,r1+y)")
       x = r2/slope
       plot!([x2, x, -x, -x2, -x, x, x2], [0, y, y, 0, -y, -y, 0],
           linecolor=:black, linewidth=0.5, seriestype=:shape, fillcolor=:gray)
       point(0, y, " y", :yellow, :left, :top)
       point(r2/slope, y, "x ", :yellow, :right, :top)
       print(2((r2 + y)*x2 - r2*x))
       point(-x2, 0, "  A", :yellow)
       point(0, 0, "O ", :yellow, :right)
       point(-x, -y, "  B", :green, :left, :top)
       point(0, -y, " C", :green, :right, :top)
       point(0, -r2-y, "    P", :green, :left, :center)
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

算額（その291）

算額（その291）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額(281)
長野県中野市片塩 大徳寺 天保9年(1838)

上下の甲円は外接しそれぞれ左右の甲円にも外接している。乙円 2 個は互いに外接し，下の甲円と容円および左右の甲円に外接している。容円は上の甲円に内接している。
甲円の直径が 125 寸のとき，容円の直径を求めよ。

半径，中心座標を以下のように決める。
甲円 r1, (0, r1), (x1, 0)
乙円 r2, (r2, y2)
容円 r3, (0, 2r1 - r3)

r1 = 125/2 であるが，r1 も未知数として以下の連立方程式を解き(x1, r2, y2, r3) を求める（それぞれの式に r1 が含まれる）。

include("julia-source.txt");

using SymPy

@syms r1::positive, x1::positive, r2::positive, y2::positive, r3::positive;

r1 = 125/2
eq1 = x1^2 + r1^2 - 4r1^2
eq2 = r2^2 + (2r1 -r3 -y2)^2 - (r2 + r3)^2
eq3 = r2^2 + (y2 + r1)^2 - (r1 + r2)^2
eq4 = (x1 - r2)^2 + y2^2 - (r1 + r2)^2
res = solve([eq1, eq2, eq3, eq4], (x1, r2, y2, r3))

   1-element Vector{NTuple{4, Sym}}:
    (sqrt(3)*r1, r1*(-92*sqrt(-11013 + 12723*sqrt(3)) - 86*sqrt(-3671 + 4241*sqrt(3)) + 4499 + 8998*sqrt(3))/13497, r1*(-13497 - 4499*sqrt(3) + 86*sqrt(-11013 + 12723*sqrt(3)) + 276*sqrt(-3671 + 4241*sqrt(3)))/13497, r1*(-sqrt(-58736/167281 + 67856*sqrt(3)/167281) - 62*sqrt(3)/409 + 627/409))

   x1 = 108.25318;  r2 = 24.13163;  y2 = 20.70279;  r3 = 42.34994
   容円の直径(2r3) = 84.69989

容円の半径は以下の式に甲円の半径を掛けたものになる。

@syms d
apart(res[1][4](r1 => 1), d) |> simplify

「算額への招待 追補1」 http://www.wasan.jp/syotai/syotai.html では以下の解が示されている。

A = ((1 + 2√Sym(3)) - 2sqrt(1+√Sym(3)))/3
@syms d
eq = ((12+2A+A^2) - 2(A + 2)sqrt(2A + 1))/(8 + 4A + A^2)

簡約化すると以下のようになるが，SymPy で求めた式より若干複雑である。

apart(eq, d) |> expand |> simplify   

いずれにせよ，甲円の直径が 125 寸のとき，容円の直径は 84.69988610132283 寸 である。

2*(125/2 * (-4*sqrt(-3671 + 4241*sqrt(3)) - 62*sqrt(3) + 627)/409)

   84.69988610132283

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 125 / 2
   (x1, r2, y2, r3) = (
       sqrt(3)*r1,
       r1*(-92*sqrt(-11013 + 12723*sqrt(3)) - 86*sqrt(-3671 + 4241*sqrt(3)) + 4499 + 8998*sqrt(3))/13497,
       r1*(-13497 - 4499*sqrt(3) + 86*sqrt(-11013 + 12723*sqrt(3)) + 276*sqrt(-3671 + 4241*sqrt(3)))/13497,
       r1*(-sqrt(-58736/167281 + 67856*sqrt(3)/167281) - 62*sqrt(3)/409 + 627/409)
   )
   @printf("x1 = %.5f;  r2 = %.5f;  y2 = %.5f;  r3 = %.5f\n", x1, r2, y2, r3)
   @printf("容円の直径(2r3) = %.5f\n", 2r3)
   plot()
   circle(0, r1, r1)
   circle(0, -r1, r1)
   circle(x1, 0, r1)
   circle(-x1, 0, r1)
   circle(r2, y2, r2, :blue)
   circle(-r2, y2, r2, :blue)
   circle(0, 2r1 - r3, r3, :orange)
   if more
       point(0, r1, " r1", :red)
       point(0, -r1, " -r1", :red)
       point(x1, 0, " x1", :red)
       point(r2, y2, "(r2,y2)", :blue, :center, :bottom)
       point(0, 2r1 - r3, " 2r1-r3", :orange)
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

Julia の挙動不審

Julia で 2 * *(4 + 6)  を入力すると，エラーなしで  2 * (4 + 6) を計算する。

julia> 2 * *(4 + 6)

20