using CSV, DataFrames, FreqTables, StatsPlots
2021 年度のプロ野球選手のポジション,生年月日,身長,体重のデータ
https://npb.jp/bis/teams/
df = CSV.read("npb.csv", DataFrame);
年齢計算関数(2021/04/01 現在)
function age(y, m, d)
res = 2021 - y
if m > 4 || (m == 4 && d > 1)
res -= 1
end
res
end
年齢の計算と,"支配下選手" をフィルタリング
using Query
df2 = df |> @mutate(年齢 = age(_.生年, _.月, _.日),
BMI = _.体重 / (_.身長 / 100)^2) |>
@filter(_.区分 == "支配下選手") |> DataFrame
年齢の分布
res = freqtable(df2[!, :年齢]);
using Plots
pyplot(grid=false, label="")
bar(names(res), res, xlabel="年齢", ylabel="人", tick_direction=:out)
BMI の分布
histogram(df2[!, :BMI], xlabel="BMI", ylabel="人", tick_direction=:out)
守備範囲でグループ化
gdf = groupby(df2, :守備位置);
using Statistics
身長,体重,BMI の分布
combine(gdf, :身長 => mean, :身長 => std,
:体重 => mean, :体重 => std,
:BMI => mean, :BMI => std,
[:身長, :体重] => cor)
# 4 rows × 8 columns
# 守備位置 身長_mean 身長_std 体重_mean 体重_std BMI_mean BMI_std 身長_体重_cor
# String Float64 Float64 Float64 Float64 Float64 Float64 Float64
# 1 外野手 180.55 5.50386 85.0643 8.93076 26.0627 2.10372 0.640489
# 2 投手 181.998 5.91158 86.0314 8.15001 25.9529 1.86002 0.649159
# 3 内野手 179.062 5.85431 83.7416 10.829 26.0598 2.58367 0.652952
# 4 捕手 177.62 4.09284 84.6962 6.15474 26.8427 1.69953 0.51652
身長と体重の散布図の描画
function correlation(df; group=df[1, 3])
plt = scatter(df[!, :身長], df[!, :体重],
markercolor=:blue, markerstrokecolor=:blue,
markeralpha=0.3, markerstrokealpha=0.3,
markersize=3, smooth=true,
xlabel="身長", xlims=(166, 202),
ylabel="体重", ylims=(64, 121),
tick_direction=:out)
title!("$group r = $(string(round(cor(df[!, :身長], df[!, :体重]), digits=3)))")
plt
end
extrema(df2[!, :身長]) # (167, 201)
extrema(df2[!, :体重]) # (65, 120)
extrema(df2[!, :BMI]) # (20.37037037037037, 36.15702479338843)
plt0 = correlation(df2, group="全選手")
plt1 = correlation(gdf[1]);
plt2 = correlation(gdf[2]);
plt3 = correlation(gdf[3]);
plt4 = correlation(gdf[4]);
plot(plt1, plt2, plt3, plt4)
savefig("fig1.png")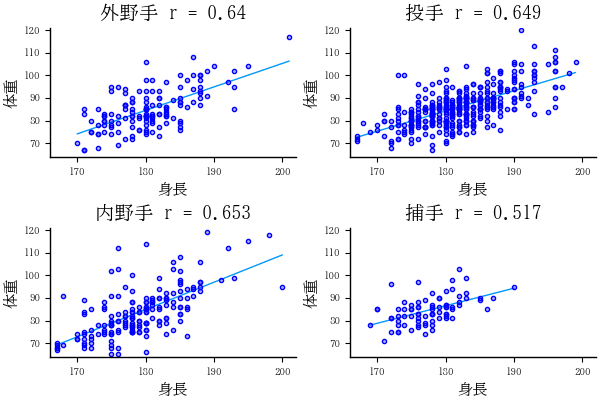
BMI のヒストグラム描画
function distributionofbmi(df; group=df[1, 3])
bmi = floor.(Int, df[!, :BMI] ./ 0.5) .* 0.5
res2 = freqtable(bmi)
plt = histogram(df[!, :BMI], bins=15, alpha=0.8,
xlims=(20, 37), xlabel="BMI",
ylims=(0, 0.35), ylabel="PDF", normalize=:pdf,
tick_direction=:out)
title!("$group Mean = $(string(round(mean(df[!, :BMI]), digits=3)))")
plt
end
plt0 = distributionofbmi(df2, group="全選手")
plt1 = distributionofbmi(gdf[1]);
plt2 = distributionofbmi(gdf[2]);
plt3 = distributionofbmi(gdf[3]);
plt4 = distributionofbmi(gdf[4]);
plot(plt1, plt2, plt3, plt4)
savefig("fig2.png")
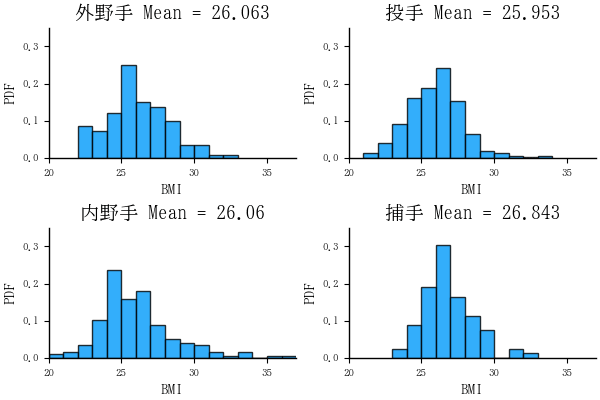
いくつかわかったこと
- 捕手は比較的小柄な選手が多い。身長は 190 センチ未満,体重は 100 キログラム未満。いわゆる漫画のドカベンタイプ(大男)のイメージではない。しかし,BMI の平均値は 26.843 と最も高いので,小さいがずんぐりしているのかもしれない。
- 身長と体重の相関係数は,捕手が 0.517 と一番低い。内野手,投手,外野手では 0.65 程度である。



















