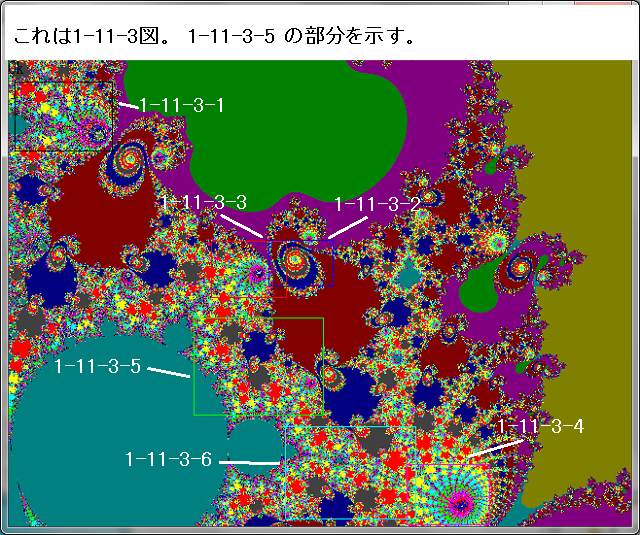
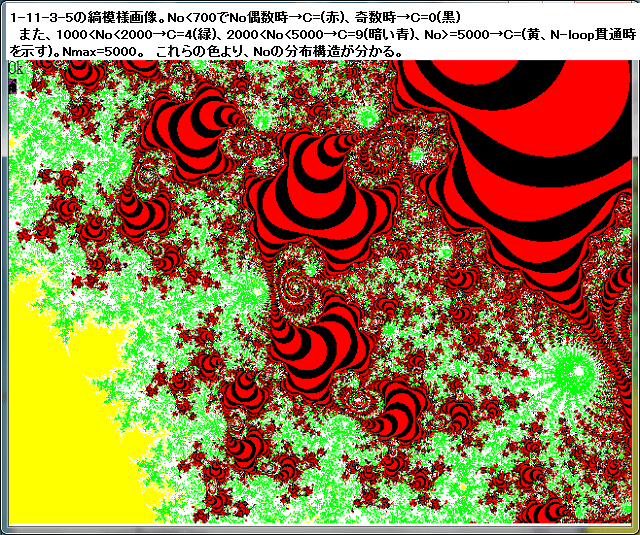
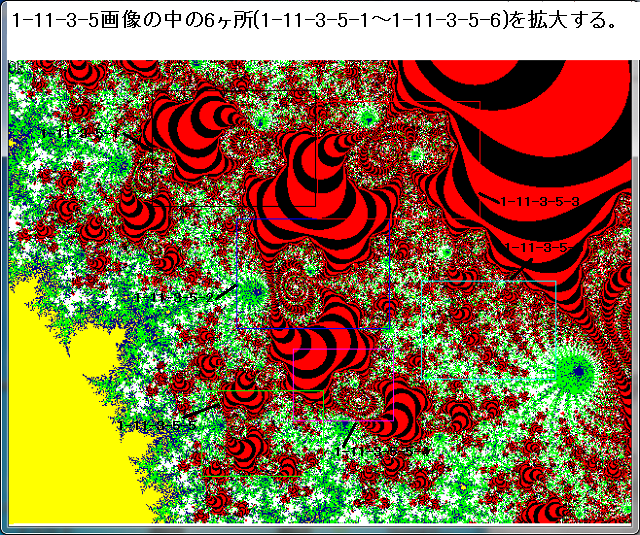
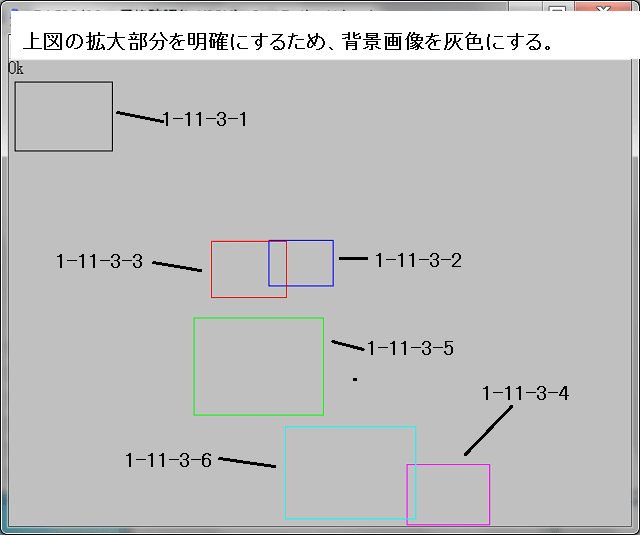
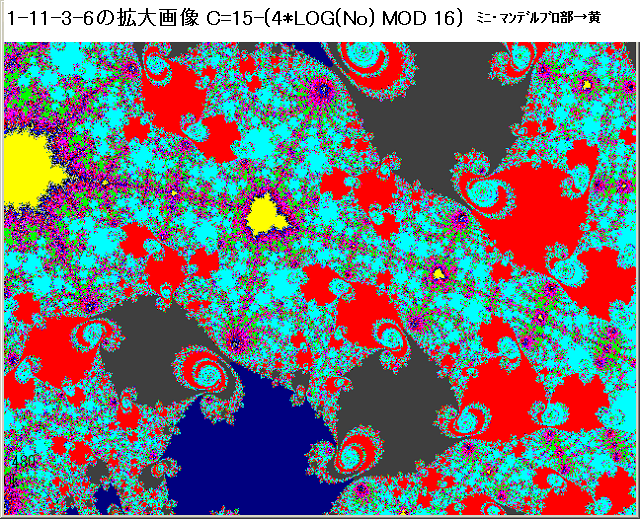
記事344に記載した、1-11-3-5-3画像の中の赤黒縞模様の興味深い個所を2個所、拡大する。
先ず、1-11-3-5-3画像の位置について再確認する。



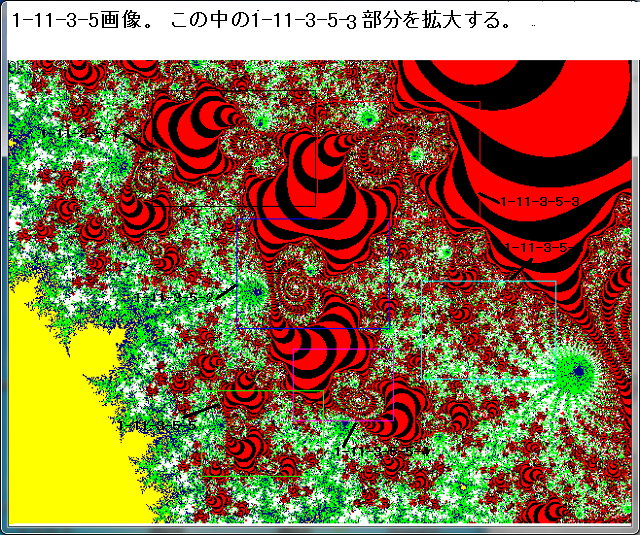



-------------------------------
上図の1-11-3-5-3-12部分、及び、1-11-3-5-3-2部分を拡大する。
また其れらの画像の1画像に対する拡大率表も示す。




----------------------------------------------------------
以下は1-11-3-5-3-12部分画像、及び、1-11-3-5-3-2部分画像についての検討である。
***
1-11-3-5-3-1画像について。
①1-11-3-5-3-1部分は、記事344で記載した、螺旋模様の本体から派生した部分が集まる個所の拡大図である。
この画像は元の1画像から、約110万倍拡大された画像である(上図の表を参照)。この画像の前の画像、即ち1-11-3-5-3画像で見られた赤黒縞模様の赤、黒の規則的反復は、(これは、Noが、1ずつ規則的に増加していくことを意味しているが) 、1-11-3-5-3-1画像では、その赤黒の反復性は無くなっていることが分かる。
②赤黒縞模様の本体から派生した部分が集まる個所(1-11-3-5-3-1画像)は、ギザギザの円状部分(2000<No<5000)から成り、その中央部に、No>5000(C=14:暗い黄)となるN-loop貫通部が存在している。この個所を更に拡大したらミニ・マンデルブロ画像が現れるかも知れない。
このN=loop貫通部(収束部分)の周囲にランダムに黒状の点が散在しているが、色の識別付がつかないので、それらの点のNoは不明。
700<N<1000の場合はプログラム上、C=No MOD 16の点は表示可能であるが、700 MOD 16=10(暗い赤)、1000 MOD 16=12(暗い緑)となり、散在する点は色から見て、No=700~1000の可能性はあるが、はっきりしたことは分からない。
***
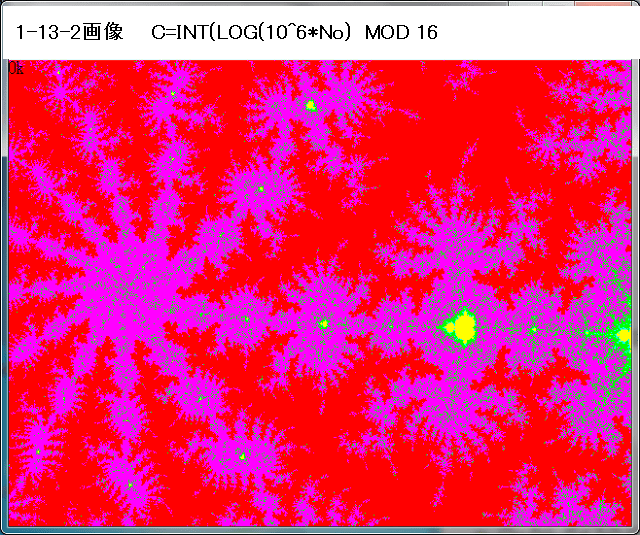
1-11-3-5-3-2画像について。
この画像の拡大率は1画像に対して約110万倍。1-11-3-5-3図での該当拡大部の赤黒縞模様構造が拡大しても同様に続いていることが分かる。
この画像は、No<700の場合、No偶数→赤、奇数→黒。
1000<No<2000→C=4(緑)、2000<No<5000→C=9(青)、N>5000→C=6(黄)としている。
Naを700以上にすれば、この縞模様は、もっと中心部へと続いていくと思われる。
中心部で散在する点があるが、上の1-11-3-5-3-1と同様に、それらの点の色の識別ができず、それらの点のNoは不明。それらの点の動きから見て、この画像の赤黒縞模様が中心部へと向かっているような暗示を受ける。
------------------------------------------------------
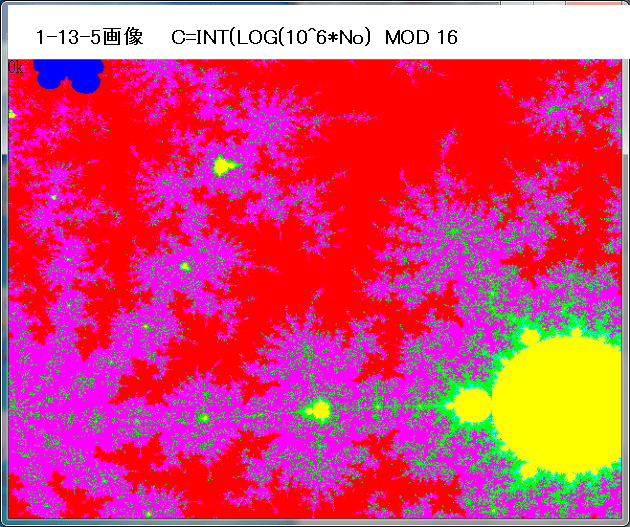
追記: 下図は、1-11-3-5-3-1画像の全てのNoに対して、Noが偶数→C=2(赤)、奇数→C=0(黒)とした場合の画像である。赤黒縞模様パターンは、上の1-11-3-5-3-1画像の黄色部分(ギザギザ部分は除く)では、縞模様パターンは認識できない。ギザギザ部分までは認識できる(オリジナル画像において)。上の1-11-3-5-3-1画像の黄色部分(ギザギザ部分は除く)では、もしかしたら、Noの「偶数・奇数」性はランダム化しているのかも知れない。