どもども。
今回は今年の京大入試理系数学の第4問をやります。
問題はこちら
http://www.yozemi.ac.jp/nyushi/sokuho/recent/kyoto/zenki/sugaku_ri/mon4.html
2の3乗根に関する問題です
(2)は大学数学で言うところの体論のカテゴリにあたるような話です。
√2が無理数であることの証明は背理法を使ってやるとうまくいく
ということは多くの人は知っているはずなので,
きっと同じ方法で上手くいくはずだ というわけで(1)は解法の方針を立てるのは
というわけで(1)は解法の方針を立てるのは
決して難儀ではないでしょう。(2)も背理法を使えばよいのですが,矛盾を導く過程が多少面倒であるようです。
 (1)
(1)
まずは一番定番であると思われる手法で証明しましょう
もしも2^(1/3)が2^(1/3)=q/pと既約分数で表現できると仮定したら
矛盾が生じてしまう,だから2^(1/3)は無理数だ

という発想ですね。
両辺を3乗することで立方根を含まない関係式が得られます。

2^(1/3)=q/p と,分数で表現するというところまでは覚えていたけれど
互いに素という条件を入れるのを忘れた!
みたいな部分で躓くことは考えられますね。
忘れてたとしても議論を進めてると,矛盾を導くところで気付くはずなんですが~
無意識的にpとqは互いに素なんだっていう前提で話を進めてると気づかないこともあるかもです
たとえば対偶をとって証明するとか,多少表現の仕方や式変形などに差異はあったとしても,
基本的に背理法を用いるのと同等の作業を行うことになるかと思います。
上の解法ではqは偶数だということでq=2Qと置いていました。
素因数分解を意識してq=(2^k)Q (k:自然数,Q:奇数)とおいてみたのが
次の解法(途中から)です。
2p^3=q^3の両辺の素因数分解に現われる因数2の指数を比較します。

次も素因数分解を利用した解法パターン。
1<2^(1/3)<2より2^(1/3)は整数ではありません。よってp>1としてよいです。
ここでpが持つ素因数aに着目します

次は今までの解法とは大きく違う部分があります。
pとqが互いに素であることを仮定しなくてもOKです
いわゆる無限降下法ってやつです。

{P_k}も{Q_k}も,構成の手順によれば無限列になるはずなのですが
実際はどんどん1/2倍されていくので有限回で整数でなくなってしまうんですね
 (2)
(2)
基本的には,有理数A,B,Cが A4^(1/3)+B2^(1/3)+C=0 を満たしていれば,A=B=C=0であることを証明することがメインになる問題です
整式P(x)をx^3-2で割った商をQ(x),余りをr(x)とおくと
r(x)は高々2次の多項式です。x^3-2で割り切れるということはr(x)=0を意味します。
r(x)=ax^2+bx+c (a,b,cは有理数)とおきましょう。
ここでa,b,cは有理数になることもきちんと証明しておくととても親切ですが,そこまで要求はされないでしょう
P(x)=(x^3-2)Q(x)+r(x)にx=2^(1/3)を代入することで
r(2^(1/3))=4^(1/3)a+2^(1/3)b+c=0が得られます。
あとはa=b=c=0を示せばいいっていうわけです
(1)のように,適当に移項して何乗かすれば両辺が有理数になればいいのですが,
なかなか厄介のようです。 4^(1/3)があるから上手くいかないのですが,これを消去するとうまくいきます


要は,A4^(1/3)+B2^(1/3)+C=0 型の式が2本あればいいんですね
1番の式に2^(1/3)を掛けて2番の式を得ていますが,他の方法でも勿論OKです。
2^(1/3)で割るとか,4^(1/3)を掛けるとか。
下の解法では両辺を2乗して2本目の式を得ています。

次は,まず冒頭で有理数A,B,Cが A4^(1/3)+B2^(1/3)+C=0 を満たしていれば,A=B=C=0であることを上記の方法などで証明してあるものとして,それを利用するという方針です。
まず整式P(x)を3つの整式の和 P(x)=P_1(x)+P_2(x)+P_3(x) に分けます。
P_1(x)は次数が3の倍数である項だけを集めてきた整式,
P_2(x)は次数が(3の倍数)+1の形である項だけを集めてきた整式,
P_3(x)は次数が(3の倍数)+2の形である項だけを集めてきた整式とします。
このように分けるのは,P_1(2^(1/3))は有理数,P_2(2^(1/3))は有理数×(2^(1/3)),
P_3(2^(1/3))は有理数×(4^(1/3))という形になるからです

ここで, A^k-B^k の因数分解を利用すると x^(3k)-2^k が x^3-2 で割り切れることに着目します。

これを利用してP(x)が x^3-2 を因数に持つことを直接導きます

次も似たような解法です。同じようにP(x)をP_1(x),P_2(x),P_3(x)に分けて,
それぞれを x^3-2 で割ったときの商と余りを直接求めます。
このときの余りがP(2^(1/3))=0の条件の下では必ず0になってしまうことを示すというやり方です
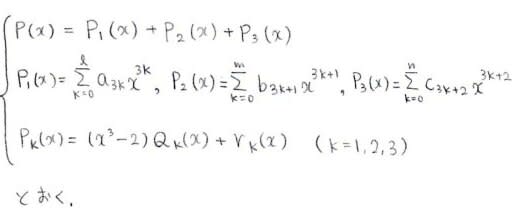

実際に筆算してみることで商と余りの形は類推することができます。
ここでは直接掛け算してその類推が正しいことを確かめてます。


後半の式の証明はメンドクサイので割愛しました
ケアレスミスが混じってたらスンマセン
あとはこれら3つの余りが0であることを言いましょう。

最後に,A4^(1/3)+B2^(1/3)+C=0 型の式の解析を用いない方法で
証明して終わります


今回は今年の京大入試理系数学の第4問をやります。
問題はこちら
http://www.yozemi.ac.jp/nyushi/sokuho/recent/kyoto/zenki/sugaku_ri/mon4.html
2の3乗根に関する問題です

(2)は大学数学で言うところの体論のカテゴリにあたるような話です。
√2が無理数であることの証明は背理法を使ってやるとうまくいく

ということは多くの人は知っているはずなので,
きっと同じ方法で上手くいくはずだ
 というわけで(1)は解法の方針を立てるのは
というわけで(1)は解法の方針を立てるのは決して難儀ではないでしょう。(2)も背理法を使えばよいのですが,矛盾を導く過程が多少面倒であるようです。
 (1)
(1)まずは一番定番であると思われる手法で証明しましょう

もしも2^(1/3)が2^(1/3)=q/pと既約分数で表現できると仮定したら
矛盾が生じてしまう,だから2^(1/3)は無理数だ


という発想ですね。
両辺を3乗することで立方根を含まない関係式が得られます。

2^(1/3)=q/p と,分数で表現するというところまでは覚えていたけれど
互いに素という条件を入れるのを忘れた!
みたいな部分で躓くことは考えられますね。
忘れてたとしても議論を進めてると,矛盾を導くところで気付くはずなんですが~

無意識的にpとqは互いに素なんだっていう前提で話を進めてると気づかないこともあるかもです

たとえば対偶をとって証明するとか,多少表現の仕方や式変形などに差異はあったとしても,
基本的に背理法を用いるのと同等の作業を行うことになるかと思います。
上の解法ではqは偶数だということでq=2Qと置いていました。
素因数分解を意識してq=(2^k)Q (k:自然数,Q:奇数)とおいてみたのが
次の解法(途中から)です。
2p^3=q^3の両辺の素因数分解に現われる因数2の指数を比較します。

次も素因数分解を利用した解法パターン。
1<2^(1/3)<2より2^(1/3)は整数ではありません。よってp>1としてよいです。
ここでpが持つ素因数aに着目します


次は今までの解法とは大きく違う部分があります。
pとqが互いに素であることを仮定しなくてもOKです
いわゆる無限降下法ってやつです。

{P_k}も{Q_k}も,構成の手順によれば無限列になるはずなのですが
実際はどんどん1/2倍されていくので有限回で整数でなくなってしまうんですね

 (2)
(2)基本的には,有理数A,B,Cが A4^(1/3)+B2^(1/3)+C=0 を満たしていれば,A=B=C=0であることを証明することがメインになる問題です

整式P(x)をx^3-2で割った商をQ(x),余りをr(x)とおくと
r(x)は高々2次の多項式です。x^3-2で割り切れるということはr(x)=0を意味します。
r(x)=ax^2+bx+c (a,b,cは有理数)とおきましょう。
ここでa,b,cは有理数になることもきちんと証明しておくととても親切ですが,そこまで要求はされないでしょう

P(x)=(x^3-2)Q(x)+r(x)にx=2^(1/3)を代入することで
r(2^(1/3))=4^(1/3)a+2^(1/3)b+c=0が得られます。
あとはa=b=c=0を示せばいいっていうわけです

(1)のように,適当に移項して何乗かすれば両辺が有理数になればいいのですが,
なかなか厄介のようです。 4^(1/3)があるから上手くいかないのですが,これを消去するとうまくいきます



要は,A4^(1/3)+B2^(1/3)+C=0 型の式が2本あればいいんですね

1番の式に2^(1/3)を掛けて2番の式を得ていますが,他の方法でも勿論OKです。
2^(1/3)で割るとか,4^(1/3)を掛けるとか。
下の解法では両辺を2乗して2本目の式を得ています。

次は,まず冒頭で有理数A,B,Cが A4^(1/3)+B2^(1/3)+C=0 を満たしていれば,A=B=C=0であることを上記の方法などで証明してあるものとして,それを利用するという方針です。
まず整式P(x)を3つの整式の和 P(x)=P_1(x)+P_2(x)+P_3(x) に分けます。
P_1(x)は次数が3の倍数である項だけを集めてきた整式,
P_2(x)は次数が(3の倍数)+1の形である項だけを集めてきた整式,
P_3(x)は次数が(3の倍数)+2の形である項だけを集めてきた整式とします。
このように分けるのは,P_1(2^(1/3))は有理数,P_2(2^(1/3))は有理数×(2^(1/3)),
P_3(2^(1/3))は有理数×(4^(1/3))という形になるからです


ここで, A^k-B^k の因数分解を利用すると x^(3k)-2^k が x^3-2 で割り切れることに着目します。

これを利用してP(x)が x^3-2 を因数に持つことを直接導きます


次も似たような解法です。同じようにP(x)をP_1(x),P_2(x),P_3(x)に分けて,
それぞれを x^3-2 で割ったときの商と余りを直接求めます。
このときの余りがP(2^(1/3))=0の条件の下では必ず0になってしまうことを示すというやり方です

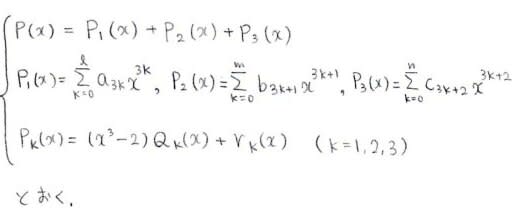

実際に筆算してみることで商と余りの形は類推することができます。
ここでは直接掛け算してその類推が正しいことを確かめてます。


後半の式の証明はメンドクサイので割愛しました

ケアレスミスが混じってたらスンマセン

あとはこれら3つの余りが0であることを言いましょう。

最後に,A4^(1/3)+B2^(1/3)+C=0 型の式の解析を用いない方法で
証明して終わります


















※コメント投稿者のブログIDはブログ作成者のみに通知されます