多次元空間へのお誘い（１５）：４次元空間で絡まる面と面の状況は？

３次元空間では絡まらない面と面

４次元空間で絡まる面と面の状況は？

第３回の記事で書いたように４次元空間では面と面、あるいは面がそれ自身で絡まりやすいのです。

ウィキペディアの「結び目理論」の項目にも「4次元空間では1次元の閉多様体である結び目はほどけてしまって役に立ちませんが、2次元の多様体である閉曲面を使ってやれば目的を果たすことができます。これを4次元結び目理論、曲面結び目理論などと呼んで結び目理論に含めることもある。」と書かれています。

また「曲面結び目理論：鎌田聖一」という本が2012年に刊行されているのを見つけました。これは４次元空間で絡まる曲面の結び目の理論を解説した本です。

４次元空間で絡まる面の姿など私たちに想像できないのはわかっていますが、僕はどうしてもあきらめきれません。その状況を３次元空間から垣間見るだけでもいいから見てみたいのです。３次元空間から見たらそれは絡まっているのでしょうか？それとも絡まっていないのでしょうか？

とりあえずひとつ次元を落として３次元空間で絡まっているひもとひもを２次元空間（平面）から見てみましょう。それはこのような状況です。



平面の世界の住人からは、このように観察されるはずですね。



平面を上にずらして絡まっている位置まで移動させると、点の位置や個数は正確ではありませんが、だいたいこのように見えます。




３次元空間を平面で切る方向はX-Y平面、Y-Z平面、Z-X平面の３通り考えられますが、どれであっても同じように赤と青の点々になることは容易に想像できます。そしてこれは３次元空間の物体を３方向にスライスして物体の一部を「立体視」したことになります。

点と点は絡まりようがないので「４次元空間で絡まる面どうしが３次元空間で観測されるひもとして見えるとき、それは絡まっているか？」の答の参考にはなりませんが、これと同じことをひとつ上の次元で試してみようというのが、今回挑戦しようとしていることです。果たしてうまくいくでしょうか？


第７回の記事で僕は４次元空間（X-Y-Z-U空間）の中にある私たちの３次元空間（X-Y-Z空間）と、もうひとつの３次元空間（X-Y-U空間）を紹介し、この２つが互いに垂直空間であることを説明しました。２つの空間はこのようなものでした。

X-Y-Z空間


X-Y-U空間


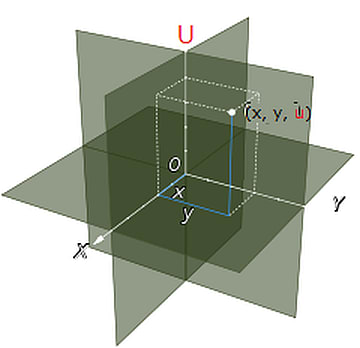
４次元空間（X-Y-Z-U空間）から３つの座標を選び出す方法はあと２つありますね。それはX-Z-U空間とY-Z-U空間という２つの３次元空間です。

つまり４次元空間にはX-Y-Z空間、X-Y-U空間、X-Z-U空間、Y-Z-U空間という４つの３次元空間が含まれていて、それらは互いに垂直空間になっているわけです。そして４次元空間をスライスしてできる「切り口」は２次元の面ではなく３次元の立体ですので、これら４つの３次元空間は４次元空間の４方向から切ったときの切り口となるのです。

４次元空間の中にある面は、３次元空間ではひも、線、点のいずれかとして観測され、そして一般的にはひもとして観測される確率が高いことは第１０回までの記事で説明しました。

４次元空間で絡まり合う面と面の姿を４つの３次元空間に映る「切り口」から観測する、いわば「超立体視」を試みるわけです。なんだかワクワクしてきます。


その状況は「３次元空間では絡まっているひもとひもとして観測されるのだろう。」という想定のもとで、僕は思考実験を始めました。

つまり４次元空間でいちばんシンプルな形で絡まっている面と面を４つの３次元空間の切り口で見た場合は、この写真の状況がどの３次元空間でも（見る角度は違っているかもしれませんが）再現されているのだと想定するわけです。



４次元空間にある赤い面と青い面を絡ませるために４つの３次元空間にある赤と青のひもを動かしながら解いていく高度な「４次元空間パズル」です。

手始めにまずX-Y-Z空間の中のX-Y平面に、次のように赤い布を置きます。X-Y平面はX-Y-U空間でも共有されていますから、X-Y-U空間で見ても赤い布が置かれている状況は同じです。



X-Y-U空間の彼に赤い布をこのように持ち上げてもらいます。私たちには認識できないU軸方向に持ち上げてもらうのです。



するとX-Y-Z空間にいる私たちには、赤い布は右端から消えていき、次の写真のようなひもとして観測されるようになります。（撮影場所が変わっていることは気にしないでください。）



ここまでは第７回の記事で解説したのと同じです。

私たちにとってこれは普通のひもですから、上下、左右の方向に曲げられるはずです。つまり曲りの自由度は２のはずですから。

とりあえず上に曲げてみます。赤いひものループを作るために必要になる曲げ方です。



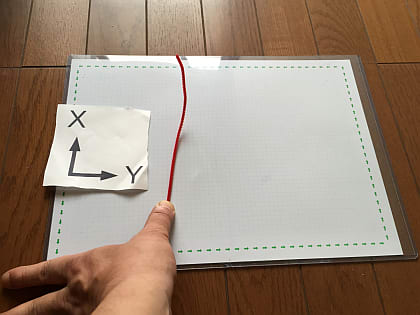
そのときX-Y-U空間にいる彼が見ている次のように斜めに立っている赤い布は、写真の向う側から消えていくように見えるはずです。

つまりこの状態から



この状態に赤い布はひもに変化していくのです。それは彼にとってZ軸方向は見えない方向だからです。（もう少し急傾斜でひもを立てて撮ったほうがよかったですね。）




次に私たちは赤いひもがX-Y平面に横たわった状態から右に曲げてみます。赤いひもはループするだけでなく、青いひもと交差するために右方向へ曲げることも必要になるからです。



そのときX-Y-U空間にいる彼には次のような赤い布がどのように変化していくかを考えたとき問題がでてきてしまうことに僕は気がついたのです。

つまりこの状態の赤い布はX-Y平面を２つの３次元空間で共有していますから、彼が見ている赤い布がX-Y平面と接している部分（線）も、私たちがひもを右に曲げると同じ方向に曲っていくわけです。



この写真でわかるように、彼にとって赤い布は６０度くらいの角度で傾斜していますから、平面に接している状態を保ちながら接している部分を右に曲げると、どうしても赤い布に「しわ」がよってしまいます。しわが寄るのは赤い布の面が伸びている方向に「押しの力」が働くからです。

「平面に接している状態を保ちながら」の理由は、２つの３次元空間で共有されているX-Y平面上でひもを右に曲げているので、彼にとっては布の下の辺を平面から離してはいけないからです。

もしこれが布ではなく下敷きのようなプラスチックの板だったらどうでしょうか？そのように曲げることができないのは明らかですよね？

つまり、私たちの３次元空間ではひもに見えるこの物体は、上方向には曲げられるものの、右方向には曲げることができない、曲りの自由度が１の「変な物体」になってしまいました。それは３次元空間にあるひもに見えていても、４次元方向につながっている物体としてひもが存在しているからだと考えられます。

これでは先に進めません。

このような困難がおきてしまう原因は何でしょうか？そしてこれを解決することはできるのでしょうか？


次回の記事では「物理的な問題」というタイトルで、問題の本質が何であるかを解説し、その次の回の記事で「問題を解決するためのアイデア」を紹介したいと思います。


応援クリックをお願いします！