多次元空間へのお誘い（７）：モノはどのように曲がる？そしてどう見える？

４次元空間にある２枚の曲面

モノはどのように曲がる？そしてどう見える？

まず、みなさんに質問させていただきます。

次の写真は４次元空間内にある１次元のひもをあらわしたものです。下の居住空間（透明プラスチックの平面）が３次元空間であることに注意してください。ひもは居住空間に突き刺さっています。居住空間は私たちが住んでいる空間という意味です。



このとき３次元の居住空間内では、このひもはどのように見えるでしょうか？１次元のひもとして観測されるでしょうか？それとも０次元の点として観測されるでしょうか？

また記事トップの写真は４次元空間内に２次元の面が２枚浮いている状況をあらわした写真です。面は両方とも下の３次元の居住空間に突き刺さっています。

さて、下の３次元の居住空間ではこれらの面はどのように見えるでしょうか？あいかわらず面として観測されるでしょうか？それとも１次元のひもとして観測されるでしょうか？

この問題が難しく思えるのは４次元空間をあらわすために用いているこのモデルが不完全であるためです。３次元空間内で４次元空間を正確にあらわすモデルは作ることができません。

今回の記事をお読みいただければ、この問題の答とどのように考えればよいのかが、わかるようになるでしょう。


まずこの写真は２次元空間にあるひもをあらわしています。平面内で１次元の物体として見えることは簡単にわかりますね。また全空間は３次元ですから、３次元空間から見ても１次元の物体です。



次は３次元空間にあるひもをあらわしています。２次元空間からは０次元の点として見えることもおわかりだと思います。線と面の交わりは「点」になるからです。



だから、２次元空間から３次元空間にあるひもを観測した場合は、０次元の点として見えるか、１次元の線として見えるかのどちらかです。一般的には前者のケースが多いでしょうから０次元の点として観測されると言ってよいでしょう。「一般的には」とはランダムにひもを３次元空間に置いた場合という意味です。


次に２次元空間に置いた２次元の面を考えてみましょう。この写真だと２次元空間から観測しても、写真全体の３次元空間から見ても２次元の面に見えます。



そして布の右端から少しずつ持ち上げてみましょう。



３次元空間から見ると布は曲面になっていますが、２次元空間から見ると正方形の面の右半分は消滅してしまい、全体として２次元空間と布の面が接触している長方形の部分だけ見えるようになったことがおわかりでしょうか？

そしてさらに布を持ち上げていくとこうなります。



２次元空間にとって、布は１次元の線になってしまいました。さらに持ち上げると布は２次元空間を離れるので、この線も消滅してしまいます。

あ、そうそう。２次元空間から布が点として見えることもあります。最初に布をこのように置けばよいのです。



布の右端の角をつまんで持ち上げていけば、最後は左端の角が点として２次元空間から見えるようになりますよね？

これまでのことをまとめると、３次元空間に置かれた２次元の面は２次元空間からは０次元の点、１次元の線、２次元の面として見えることになります。そして一般的には１次元の線として観測されると言ってよいでしょう。「一般的には」とはランダムに面を３次元空間に置いた場合という意味です。


ところで、私たちはX軸、Y軸、Z軸の方向に伸びている３次元空間に住んでいます。たとえば私たちの「部屋」はこの図の直方体のようなものです。この部屋の「床」はX軸とY軸が伸びている平面ということになります。



私たちの３次元空間はそのまわりに存在する４次元空間に含まれています。４次元空間はX軸、Y軸、Z軸、U軸の方向に伸びている空間です。そして４次元空間にとってその４つの軸は「公平」です。ですのでこの４次元空間には「X軸、Y軸、U軸の方向に伸びている３次元空間」もあるはずです。それはこのような空間のことです。



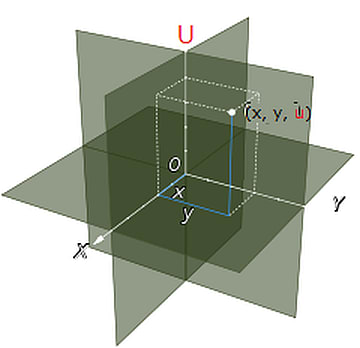
この空間は私たちにとってパラレルワールド（並行空間）ではありません。名前を付けるとすれば「バーティカルワールド（垂直空間）」という呼び方がふさわしいでしょう。この３次元空間は私たちの３次元空間と直交しているのです。

線と線が直交したり、面と面が直交することは小学校で学びますが、空間と空間が直交するというのは面白いですよね。そしてこの２つの３次元空間はX-Y方向に広がる「床」を共有していることにも気付きます。

つまり２つの部屋の中は別々の空間なので、それぞれの空間にいる生物はお互い相手の存在が見えないわけですが、私たちが床に落書きをすると垂直空間に住んでいる人は床に急に落書きがあらわれるのでびっくりするわけです。また彼が床に落書きをすると、今度は私たちがびっくりすることになります。（数学としての話です。現実にそうなると言っているわけではありません。）彼は４次元方向（U軸の方向）を認識しているので、私たちにとって彼は４次元方向の空間にいることになります。


では、なぜ彼の住んでいる３次元空間を「垂直空間」と呼ぶのでしょうか？それは次のように１つ次元数を減らして考えるとわかります。

まず、ふつうの３次元空間を考えます。３次元空間はX-Y-Z軸の方向に伸びています。３次元空間にとってはX軸、Y軸、Z軸はどれも「公平」です。

３次元空間には２次元の空間が含まれています。たとえばX-Y軸の方向に伸びている２次元空間（面）とY-Z軸の方向に伸びている２次元空間（面）がありますよね。これをそれぞれ私たちは「床」と「壁」と呼んでいるわけです。



床と壁は直角に交わっています。２次元の平面と平面が直交している状況です。だから床に対して壁はバーティカルワールド（垂直空間）に相当します。直交する平面（床）と平面（壁）は１本の直線（床と壁が交差している直線）を共有しています。

４次元空間にとって私たちの３次元空間（X-Y-Z空間）と、もうひとつの３次元空間（X-Y-U空間）は（３次元ではありますが）床と壁のようなものです。ですから３次元空間どうしが直交していると考えるわけです。

同様にして５次元空間にはお互いに直交する４次元空間がありますし、６次元空間にはお互いに直交する５次元空間があります。次の組み合わせはその例です。

- ５次元空間（X-Y-Z-U-V空間）では４次元空間（X-Y-Z-U空間）と（X-Y-Z-V空間）が直交している。

- ６次元空間（X-Y-Z-U-V-W空間では５次元空間（X-Y-Z-U-V空間）と(X-Y-Z-U-W空間）が直交している。

さらに部屋の床（２次元）と柱（１次元）も直交することができますよね？次元の異なる空間どうしも直交できるのです。

たとえば６次元空間と４次元空間から直交する空間の組合せを選び出すことができるのです。そして２つの空間が共有する空間も多次元になり、その次元数は組み合わせる空間の軸をどのように選ぶかによって異なってきます。

直交するのはこれまで直線や平面だけでしたが、このようにして直交の概念を大幅に拡張（一般化）することができました。


さて、垂直空間に住んでいる彼に私たちが行なった「布の引き上げ」の実験をしてもらうことにしましょう。

同じ写真を使いますが、今度は持ち上げる方向は彼にとっての上方向（U軸方向）、つまり私たちから見れば４次元の方向です。まず、垂直空間の彼は布をこのように置きます。



私たちと彼は「床」を共有しているので、私たちから見ても平面（２次元）に布が置かれているように見えます。

そして彼は布の右端から少しずつ持ち上げていきます。



すると私たちにはどう見えるでしょうか？

U軸方向は私たちには見えない世界ですので、布は右から少しずつ消えていくように見えるはずです。布はまったく持ち上がるようには見えません。なぜなら持ち上げる方向はU軸方向であってZ軸方向ではないからです。

布が消えていく様子はもやもやと煙のように消えるのではなく、消えている部分と残っている部分がはっきりわかれて見える感じになります。

正方形の布はだんだんと細長い長方形になり、やがて１本の線になってしまうことがおわかりでしょうか？



そして彼がさらに布を持ち上げると、私たちの世界から布は完全に見えなくなってしまいます。

これが４次元空間に置かれた２次元の物体（面）を３次元空間で私たちが見る状況なのです。一般に４次元空間に置かれた２次元の物体は３次元空間では線として観測されます。

４次元空間に置かれた２次元物体が曲面の場合、私たちは３次元空間に赤いひもがふわふわ漂っているように見えます。不思議な感じですね。

ところで２次元の布が私たちに点として見えることもあります。垂直空間の彼が最初に布をこのように置けばよいのです。彼は正方形の右側の角をつまんでU軸方向に持ち上げていくわけです。



垂直空間の彼にとって、これらの実験は私たちがX-Y-Z空間で行なっているのと全く同じになので、彼は何の不思議も感じないわけです。


次に３次元空間に３次元の物体（立方体）を置いた状況で同じことをしてみましょう。といっても３次元空間で立方体を曲げることができませんから、私たちにはこれ以上どうすることもできません。



そこで３次元の垂直空間にいる彼にお願いして、４次元方向（U軸）方向に持ち上げてもらうことにします。私たちの３次元空間は４次元空間に含まれているので、曲がりの自由度が１つあるのです。これがU軸方向に持ち上げるということになります。

３次元の垂直空間にいる彼とは床だけを共有しているので、彼にとってこの物体は２次元（正方形）に見えます。その端を持って彼が引き上げると立体が現れるので彼は驚きます。けれども彼は気を取り直して持ち上げ続けます。

私たちに見える立方体の変化はどのようなものでしょうか？右のほうから垂直にスライスしたように、どんどん消えていくはずです。４次元方向（U軸方向）は私たちには見えないのですから。

そして立方体は直方体に変化しながらどんどん薄くなっていきます。残っている部分と消えてしまった部分の境ははっきりしていることでしょう。

そして最後に直方体は完全に薄くなり、最初にあった立方体の左側の面だけが「正方形」として残ることになります。彼がU軸方向への引き上げ操作を続けると、しまいに立方体は完全に私たちの空間から消滅します。

私たちにとって立方体は３次元空間に置かれていると同時に全体空間として４次元空間の中に置かれています。最初は私たちの３次元空間に立方体は完全に含まれていましたが、４次元方向へ曲げることは、４次元空間に一般的な配置で立方体を置くことに相当します。つまり４次元空間に一般的な配置で置かれた３次元の物体は２次元物体（面）として３次元空間から観測されることになります。

一般に４次元空間にある物体は、３次元空間には空中を浮遊する曲面のように見えます。これもやはり不思議な感じがしますね。

ところで４次元空間に置かれた立方体が、私たちの３次元空間から１次元物体（直線）に見えることもありえます。それは垂直空間の彼が次のように立方体を置いて、U軸方向への引き上げをする場合です。スライスするように物体は右から消えていきます。最後に残るのは左端の直線だけですよね。



また４次元空間に置かれた立方体が、私たちの３次元空間から０次元物体（点）に見えることもあります。それは垂直空間の彼が次のように立方体を置いて、U軸方向への引き上げをする場合です。スライスするように物体は右から消えていきます。最後に残るのは左端の角の点だけです。





さて、この記事の冒頭でみなさんに質問させていただいた件ですが、もう答はおわかりでしょうか？

４次元空間に次のように置かれた１次元物体（線）が、３次元空間からどのように見えるか？という質問です。



これは次のように考えるとわかります。この写真のように布の一部が線だと考えればよいのです。



上の例で、この布を右端を持って４次元方向（U軸方向）に持ち上げれば、最後に残るのは布の左側の端の１次元の線でした。そして布の上に置いたひもだけに注目すれば、最後に残るのが０次元の点であることがわかります。

ですので、正解は「０次元の点に見える。」です。


また記事トップに掲載した写真の問題はもうおわかりですよね。４次元空間に浮かんだ２枚の２次元物体（面）が３次元空間からどう見えるかという問題です。



正解は「１次元の線に見える。」です。この写真のような状況では、３次元空間にふわふわと青い線と赤い線が１本ずつ浮遊しているように見えることになります。


ここまでのことをまとめると次のようになります。結果としてはシンプルですね。

- ４次元空間に１次元物体を置くと一般的に３次元空間からは０次元の点として観測される。

- ４次元空間に２次元物体を置くと一般的に３次元空間からは１次元の曲線として観測される。

- ４次元空間に３次元物体を置くと一般的に３次元空間からは２次元の曲面として観測される。


ところで私たちはすでに３次元以下の空間で次のことを経験的事実として知っています。これらは一般常識ですよね。（注意: 現実の物体どうしはぶつかってしまうので交われません。以下の例はあくまで幾何学の対象としての点、線、面、立体のことなので交わってもよいのです。）

- 線と線の交わりは点、線と面の交わりは点

- 面と面の交わりは線、線と立体の交わりは線

- 面と立体の交わりは面

- 立体と立体の交わりは立体

これらはそもそも物体どうしの関係にすぎませんから、物体を取り巻いている空間の次元数とは無関係です。だから４次元以上の空間でも成り立っているはずです。

赤文字にした箇所を物体、青文字にした箇所を空間と考えれば、次のようになりますよね。

４次元空間では「線と立体の交わりは線」、言い換えると「１次元物体を３次元空間で見ると１次元物体として観測される。」となり、当たり前のことを言っているわけですが、今回求めた結果と矛盾します。

そして４次元空間では「面と立体の交わりは面」、言い換えると「２次元物体を３次元空間で見ると２次元物体として観測される。」となり、当たり前のことを言っているわけですが、今回求めた結果と矛盾します。

さらに４次元空間では「立体と立体の交わりは立体」、言い換えると「３次元物体を３次元空間で見ると３次元物体として観測される。」となり、当たり前のことを言っているわけですが、今回求めた結果と矛盾します。

この矛盾はどのように解釈したらよいでしょうか？

せっかく説明をすべて理解したと思ったのに、振り出しに戻された気分になってしまいますよね。でもこの矛盾を解決することは、理解を確実なものにするためにはとても大切なことなのです。

この謎解きはみなさんへの宿題とさせていただきます。

なにせイメージしにくい多次元空間でのことですから、論理的にどうなるのか注意して一歩ずつ考えを進めることが大切です。


実をいうと今回の記事には重大な２つの問題がひそんでいます。それはまだ明かさず、この連載記事の最終回に近いところで明らかにし、解決するためのアイデアを紹介させていただくことにします。申し訳ありませんが、それまでお待ちください。


次回の記事では、今回の記事で宿題とさせていただいた件について解説いたします。


応援クリックをお願いします！