大人の数学教室132(三角比⑦)

【第7章】

(7)特別な角の三角比

①θ=0° P(1,0), OP=1

sin0°=0,cos0°=1, tan0°=0

②θ=90° P(0,1) OP=1

sin90°=1,cos90°=0, tan90°はなし

③θ=180° P(-1,0) OP=1

sin180°=0, cos180°=0, tan180°=0

❲180°-θ の三角比❳

0°<θ<90° のとき、

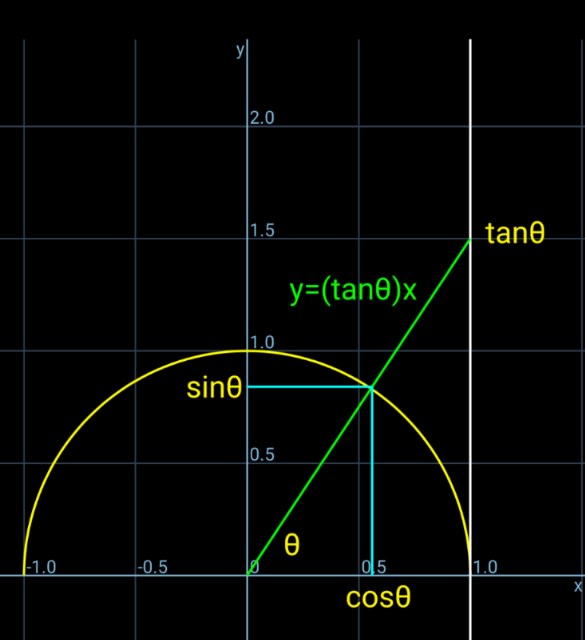
点P は第1象限の点でP(b,a) とする。

sinθ=a/OP, cosθ=b/OP, tanθ=b/a

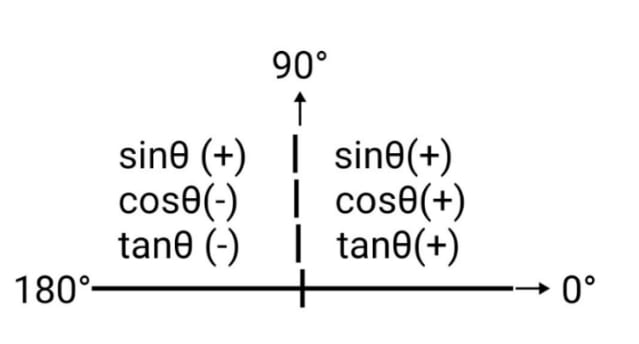
90°<180°-θ<180° だから、

点P’ は第2象限の点で、x軸に垂線を引いてx 軸との交点をQ’ とすれば、△OPQ≡△OP’Q’ なので、P’(-b,a)

sin(180°-θ)=b/OP, cos(180°-θ)=-a/OP

tan(180°-θ)=-a/b

したがって、

sin(180°-θ)=sinθ

cos(180°-θ)=-cosθ

tan(180°-θ)=-tanθ

90°<θ<180° のとき、

α=180°-θ とおくと、0<α<90° で、

90°<180°-α<180° だから、上の結果より

sin(180°-α)=sinα

→ sinθ=sin(180°-θ)

→sin(180°-θ)=sinθ

cos(180°-α)=-cosα

→ cosθ=-cos(180°-θ)

→cos(180°-θ)=-cosθ

tan(180°-α)=-tanα

→ tanθ=-tan(180°-θ)

→ tan(180°-θ)=-tanθ

180°-θ の三角比

sin(180°-θ)=sinθ

cos(180°-θ)=-cosθ

tan(180°-θ)=-tanθ

この式を利用すると、鈍角の三角比を鋭角の三角比で表すことができる。三角比の表を利用すれば、値が分かる。

例)sin126°=sin(180°-54°)=sin54°

④ θ=120°=180°-60°

sin120°=√3/2, cos120°=-½,

tan120° =-√3

⑤ θ=135°=180°-45°

sin135°=1/√2, cos135°=-1/√2,

tan135°=-1

⑥ θ=150°=180°-30°

sin150°=½, cos150°=-√3/2,

tan150°=-1/√3

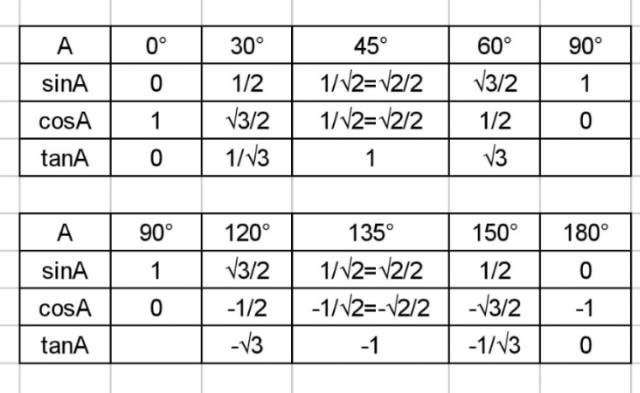
特別な角を表にすると、

大人の数学教室131(三角比⑥)

【第6章】

(6)角の拡張

一般の三角形で利用できるようにしたい。

以下△ABC と表すときは、一般の三角形とする。(直角三角形とは限らない。)

90°より小さい角を「鋭角」という。

90°より大きい角を「鈍角」という。

❲座標を利用した三角比の定義❳

点P(b,a) を第1 象限の点とする。点Pからx 軸に垂線を引き、x軸との交点をQ とする。△OPQ は、角Qが直角な直角三角形になる。r=OP, ∠POQ=θ とすると、

sinθ=a/r, cosθ=b/r, tanθ=b/a

ここで、(※)

sinθ=(Pのy座標)/OP

cosθ=(Pのx座標)/OP

tanθ=(Pのy座標)/(Pのx座標)

となっている。

原点O を中心に半径rの半円を考える。

x軸上の正の部分の交点をS とする。

点Pが半円上にあるとし、∠SOP=θ とすると、(※)によって定義する。直角三角形のできないときも三角比を考えることができる。

直線OP の傾きが tanθ である。

半径1 の半円で考えると、

点Pの座標は、P(cosθ,sinθ) となる。

❲三角比の符号と値の範囲❳

0°≦θ≦180°のとき、

0≦sinθ≦1

-1≦cosθ≦1

tanθはすべての値

大人の数学教室130(三角比⑤)

【第5章】

(5)三角比の相互関係①

tanA=BC/AC=sinA/cosA …①

三平方の定理より、(AC)^2+(BC)^2=12

(sinA)^2+(cosA)^2=1 …②

② の両辺を(cosA)^2 で割ると、

(sinA)^2/(cosA)^2+1=1/(cosA)^2

① より、

(tanA)^2+1=1/(cosA)^2 …③

三角比の相互関係

① tanA=sinA/cosA

② (sinA)^2+(cosA)^2=1

③ 1+(tanA)^2=1/(cosA)^2

三角比の1つから他の2つを求めることができる。

(i) sinA →②→ cosA →①→ tanA

(ii) cosA →②→ sinA →①→ tanA

(iii) tanA→③→ cosA →①→ sinA

例)cosA=4/5のとき、sinA, tanAの値を求めよ。

(sinA)^2+(cosA)^2=1より、

(sinA)^2=1-(4/5)^2=9/25

0＜sinA＜1より、sinA=3/5

tanA=sinA/cosA=(3/5)/(4/5)=3/4

例)tanA=2のとき、sinA, cosAの値を求めよ。

1/(cosA)^2=1+(tanA)^2=1+2^2=5

(cosA)^2=1/5

0＜cosA＜1より、cosA=1/√5=√5/5

sinA/cosA=tanAより、

sinA=cosA×tanA=(2√5)/5

❲90°-A の三角比❳

△ABC において、B=90°-A

sinB=AC/AB=cosA

cosB=BC/AB=sinA

tanB=AC/BC=1/tanA

よって、

sin(90°-A)=cosA

cos(90°-A)=sinA

tan(90°-A)=1/tanA

大人の数学教室129(三角比④)

【第4章】

三角比の値②

特別な角以外の三角比は、角A を1度刻みに考えてまとめたもの「三角比の表」を利用する。

(表を覚えなくてもよいが、活用法は覚えよう！)

表の利用

(i) 角から三角比の値を見つける。

(ii) 三角比の値から角を見つける。

表の特徴

・ 表の角は、0°から90°までである。

・ sinAは0→1の範囲で、増えている。

・ cosAは1→0の範囲で、減っている。

・ tanAは0→ の範囲で、増えている。

・ tan90° はない。

・ sinAの並びとcosAの並びは逆になっている。

具体例

(i) Aから三角比の値を見つける。

sin13°

Aの列で13を探す

その横の3つの数から探す

(sin,cos,tanの順に並んでいる)

sin13°=0.2250

(ii) 三角比の値から角を見つける。

cosA=0.3907

cosAの列で0.3907を探す

その横のAを探す

A=67°

大人の数学教室128(三角比③)

【第3章】

(3)三角比の値①

特別な角の三角比の値

①正三角形ABCで、辺BC の中点をM とする。三角形ABM は、角M が直角の直角三角形になる。それぞれの角は、90°, 30°, 60° で、辺の長さは、2,1,√3 である。

sin30°=½, cos30°=√3/2, tan30°=1/√3

また、

sin60°=√3/2, cos60°=½, tan60°=√3

② 正方形ABCD で、三角形ABD は、角Aが直角である直角三角形になる。それぞれの角は、90°, 45°, 45°で、長さは、1,1,√2 である。

sin45°=1/√2, cos45°=1/√2, tan45°=1

(三角定規は2種類あるが、正三角形と正方形を半分に割った直角三角形で、

角が(90°,60°,30°),(90°,45°,45°)である。)

表にすれば、

この表はしっかり覚えよう！