麻雀戦略 目次

・当blogでの麻雀を打つ目的

・ペンチャンvs浮き牌　その1
・ペンチャンvs浮き牌　その2
・ペンチャンvs浮き牌　その3
・ペンチャンvs浮き牌　その4　

・ツモ山読みの効果　その1　
・ツモ山読みの効果　その2
・ツモ山読みの効果　その3　

　赤入り麻雀での押し引き
1.序論
1.1　麻雀での押し引き研究の歴史　
1.2　期待値の導入　
1.3　統計データの扱い　
2.方法
2.1　方法
3.結果と考察
3.1　他家先制リーチでの押し引き　
3.2　追いかけリーチ　安い両面か高い愚形か？　
3.3　他家先制リーチのドラ別あがり点数　
3.4　他家追いかけリーチ平均点数 　　
3.5　通常鳴き手に対する押し引き　

3.5 通常鳴き手に対する押し引き

3.5.1　はじめに
今まではリーチに対する押し引きを考えてきましたが
今回から鳴き手に対する押し引きを考えます。
リーチと違い、鳴き手はフーロした情報が増えるので
がむしゃらに統計を基に押し引きの考察をするのは
あまり精緻ではないかもしれませんが、
「リーチと同じように相手の点数の高さが読めない」鳴き手も存在するので
そういうときに使えると思います。

また、鳴き手はリーチと違ってはっきりテンパイしたかどうか分からない事から
あがり率や振込み率などのパラメーターが解明されていないのですが、
とりあえずリーチと同様に
「他家が100％鳴き手をテンパイしているとわかっている」と仮定したうえで
押し引きを考察します。

少なくとも上記仮定のもとで押し引きを計算したときに
押すべきという結果が出た領域については、
現実の麻雀でも押すべきだとわかります。
なぜなら、上記の仮定は現実の麻雀では有り得ないので、
(裸単騎以外は)
相手がテンパイしていないのに降りてしまい
手を進められ、あがられてしまう可能性が
実際には加わるからです。



3.5.2　通常鳴き手とは
「通常鳴き手」とは鳴き手の内、
・タンヤオ
・染め手
・対々和
・ドラポン
以外の鳴き手のことをいいます。
主に、役牌を鳴いたときですね。
他には、喰い三色、喰い一気通貫、鳴きチャンタなどが含まれます。


3.5.3　ドラ別のあがり点数分布
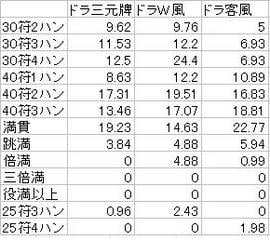
図3.5.1と図3.5.2はドラ別に集計した、通常鳴き手のあがり点数の分布です。
各点数が何％の割合だったかを表しています。


図3.5.1　通常鳴き手あがり点数分布　その1
　　　　サンプル合計数以外の数字の単位は％　
　　　　約14000局の集計結果


図3.5.2　通常鳴き手あがり点数分布　その2

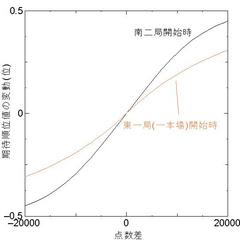
図3.5.3は上記の表をグラフにしたものです。


図3.5.3　通常鳴き手あがり点数分布のグラフ

それぞれのサンプル数は十分とはいえません。
特にドラＷ風のサンプル数は少な過ぎるので
参考程度に見てください。
それでも、この程度のサンプル数で断言できることがあって
「30符3ハンの手はドラが字牌のときよりドラが数牌のときの方が多い」
ということです。
30符3ハンの手は、ドラが数牌のときだと20％オーバーくらい
ドラが字牌のときだと15％弱くらいだと推測できます。
なぜかはわかりません。不思議ですね。

他の数字は、統計揺らぎ程度の違いです。
僕はドラの違いでもっとはっきり分布が違うのかと思っていたのですが、
意外とドラに依らず似たような分布です。

その他の特徴としては、やはり7700点以上の手の数が減ってます。
先制リーチのときが38％くらいだったのですが、
通常鳴き手だと7700以上の手はその半分くらいに減ります。


3.5.4　通常鳴き手平均点数
図3.5.1と図3.5.2から平均得点を求めます。
ドラに依らず得点分布はほぼ変わらないので、全体を平均すると
平均得点は子で3622.138点となりました。
親だと1.5倍で5433.207点です。
もしも「他家の一人が鳴き手で100％テンパイしているのがわかる」と仮定したときに
自分がテンパイしたら押すか引くかですが、

(1)自分が子
鳴いてる他家が子でも親でも結論は同じになりました。
愚形リーチのみで追いかけるかどうかがぎりぎり境界となりますが、
実際には鳴いてる他家が100％テンパイしてるか判断できないので
面前テンパイはすべてリーチでいいでしょう。
自分も鳴いている場合は、
両面は全て、愚形は2000点以上なら全ツッパとなります。
リーチと違って、他家がツモっても面前ツモの1ハンがつかないので
ベタオリの期待値も高めに出ました。

(2)自分が親
自分の手の点数、待ち、面前or鳴いてる状態に依らず、
テンパイしたなら全ツッパです。
親ッパネの影響は、他家が鳴き手のときも大きいようです。


ただし、繰り返しになりますが、上記はあくまで
「他家の鳴き手が100％テンパイしたとわかる」という仮定のもとでの話で、
実際にはテンパイに見えてもノーテンかもしれない可能性を考慮すると、
「他家が通常鳴き手でテンパってそうでも
自分もテンパイしたら、どんな手でも全ツッパ」
が正しい気がします。


　前へ　　　目次へ

3.4 他家追いかけリーチ平均点数

3.4.1　はじめに
ここまでは他家の先制リーチについて考察してきました。
では、他家の追いかけリーチについてはどうなのでしょうか？
正直、他家追いかけリーチに対する押し引きは
あまり実用性がありません。
というのも、三人リーチや四人リーチはそんなに
発生しないからです。
また、他家が二人以上リーチしている状態で
自分が押したときや降りたときの
あがり率や振込み率などの値は、現在判明していません。
(とつげき東北さんが書いたような
　一人リーチに対するシミュレーションプログラムと
　同じようなものを書けばいいのですが、
　具体的なコードが明らかになっていない。)
ただ、他家追いかけリーチの平均点数について調べたので
参考までに掲載します。


3.4.2　方法
自分以外の他家の追いかけリーチの点数を記録しました。
すべてロンしたと仮定したときの得点分布です。
ただし、裏ドラによるハン数の増加は含めていますが、
リーチ一発であった場合は一発を含めず
また、河底やリンシャンであがった場合も
河底やリンシャンは含めない
ハン数で記録しました。



3.4.3　結果
図3.4.1は他家の追いかけリーチで
ずべてロンしたと仮定しときの得点分布です。


図3.4.1　追いかけリーチ得点分布
　　　　　約12000局の集計、主なものを示しました

図3.4.2は他家先制リーチの得点分布と
追いかけリーチの得点分布のそれぞれを
総数で割って、割合で示し比較した図です。


図3.4.2　先制と追いかけ、それぞれの得点分布割合

グラフ化したものが、下の図3.4.3です。


図3.4.3　先制と追いかけ、それぞれの得点分布割合グラフ

確率の揺らぎはそれぞれのサンプル総数から求められて、
先制リーチの方は1％強、追いかけの方は約3%なので
満貫や40符3ハンに関しては
追いかけの方が多くなると、ほとんど言いきってよいでしょう。
また、追いかけ時の平均得点は子で6492.6点となりました。
先制リーチのときは子で5671.0点だったので、
800点ほど高くなります。
とはいえ、点数の増加は1.14倍程度なので大差がありません。
先制リーチの平均が40符3ハンで
追いかけリーチの平均が50符3ハンだと
考えとけばいいでしょう。


3.4.4　まとめ
追いかけリーチは先制リーチに比べ
若干平均点数が高くなるが、
同じくらいとみなして問題ない。


　前へ　　次へ　　目次へ

3.3 他家先制リーチのドラ別あがり点数

3.3.1　仮説
ここまで他家先制リーチのあがり点数に関して
ドラの区別なしの平均を用いてきました。
しかし、実際にはドラの違いによって
ドラの使いやすさが変わることから
リーチのあがり点数も変化すると予想されます。
ひいいさんによると、牌の使いやすさは以下のようになっているそうです。[1]
ひいいの麻雀研究・２－１０－２統計分析
以上のレポートから
「字牌がドラのときは数牌がドラのときよりリーチ点数が下がり、
またドラが数牌のときでも5に近いほどリーチ点数が高くなる」
という仮説を立てました。
では、この仮説は果たして正しいのでしょうか？
ドラの違いによってあがり点数を調べてみました。


3.3.2　方法
ドラの種類は以下のように分けました。

・1、9(6種牌)
・2、8(6種牌)
・3、7(6種牌)
・4、6(6種牌)
・5　 (3種牌)
・三元牌(3種牌)
・Ｗ風(1種牌)
・客風(3種牌)

以上のドラの種類ごとに、他家先制リーチでの
出あがりしたと仮定したときのあがり点数を記録しました。
ただし、裏ドラによるハン数の増加は含めていますが、
リーチ一発であった場合は一発を含めず
また、河底やリンシャンであがった場合も
河底やリンシャンは含めない
ハン数で記録しました。



3.3.3　結果
図3.3.1にドラが数牌のときの結果を
図3.3.2にドラが字牌のときの結果を示します。
調査対象は麻雀格闘倶楽部半荘A1と黄龍闘技場AAA半荘の約6000局です。


図3.3.1　ドラが数牌のときの先制リーチあがり点数の分布
　　　　　数字の単位は％


図3.3.2　ドラが字牌のときの先制リーチあがり点数の分布
　　　　　数字の単位は％

わかりやすくグラフ化したものが、下の図3.3.3です。


図3.3.3　ドラ別の先制リーチあがり点数のグラフ

各ドラにおけるサンプル数は以下の通りです。(右数字)

・1、9(6種牌)　　235
・2、8(6種牌)　　238
・3、7(6種牌)　　211
・4、6(6種牌)　　200
・5　 (3種牌)　　 92
・三元牌(3種牌)　104
・Ｗ風(1種牌)　　 41
・客風(3種牌)　　101

「ドラがW風のとき」はサンプル数が少ないので
他のデータと少し異なる振る舞いを示しています。
また、「ドラがW風のとき」以外でもところどころ
異常値が見られますが、統計学的に自然な範囲に収まっています。
サンプル数が十分ではないので、断定的なことは言えませんが
とりあえず「ドラの違いによってリーチ点数は統計的には変わらないのではないか」と
考えられます。


3.3.4　考察
「字牌がドラのときは数牌がドラのときよりリーチ点数が下がり、
またドラが数牌のときでも5に近いほどリーチ点数が高くなる」という仮説が
否定されるのではないかという結果が出てきましたが、
その原因はなんでしょうか？
考察してみるとこんなところでしょうか。

1.高い手はダマにするから
ドラが何であろうと、高い手になったらダマで待ちます。
ドラだけで役なしの高い手になることは
あまりありません。

2.赤ドラがあるから
ドラが数牌だろうが字牌だろうが
赤ドラの使いやすさは変わりません。
よって、ドラが数牌と字牌のときでのリーチ時の点数差が
あまり変わらなくなると。
もしかしたら、赤なし麻雀ではドラが数牌と字牌のときで
リーチ時の点数差が明確に出るのかもしれません。
(赤なしでのドラ別リーチあがり点数は、まだ報告されていません。)


　参照
[1]ひいい　「ひいいの麻雀研究HP」

　前へ　　　次へ　　目次へ

3.2 追いかけリーチ、安い両面か高い愚形か？

一日遅れの更新ですみません。

3.2.1　先制リーチでの待ち取り
安くても手広い待ちにするか
狭いけれども高い待ちにするか、
テンパイ時での待ち取りに迷うことがあります。
自分以外の他家がテンパイしていない場合、
愚形待ちのあがり確率は
両面待ちのときの半分にはならないので、
(参考：ペンチャンvs浮き牌　その3)
平場では期待値的に考えて、点数が2倍になるならば
広くて安いテンパイより狭くて高いテンパイの方が優秀となります。
では、他家の先制リーチが入っているときではどうでしょうか？
先ほどとは違い、振り込んで点数を失う可能性も考えなくてはいけません。
この場合でも、狭くて高い方が優れているのでしょうか？
計算してみましょう。


3.2.2　両面待ちと点数2倍の愚形待ちでの追いかけ
よくあるパターンとしては下の図3.2.1のケースがあります。

　　ドラ
　　図3.2.1　待ち取りに迷う牌姿

待ち取りの方法は以下の2通りになります。
パターン1　赤五萬切り　裏ドラなしで1300点の両面待ち
パターン2　　 二萬切り　裏ドラなしで2600点の愚形待ち

他家がテンパイしていないならば
先述の通り狭くて高い方の二萬切りが正しいのですが、
今、子の他家が先制リーチしているとしたらどうでしょうか？
自分も子で、他家のリーチの点数は「3.1　他家先制リーチでの押し引き」で
書いたように、ロンで5671.0点ツモで7294.0点とします。
また、祝儀は無しです。

計算結果が下の図3.2.2です。

　　　　　　　
図3.2.2　広くて安い場合と狭くて高い場合での追いかけ期待値

広く安い赤五萬切りがほんの少しだけ期待値が上です。
せいぜい数百点差なので、ほぼ同じと言ってもいいと思います。
なので、両面待ちか点数2倍の愚形かは細かな状況で変化します。

　状況1
今の計算は相手リーチに対し無筋牌を切って追いかけという場合を
計算しているので、
相手のリーチに対し五萬が無筋で二萬が現物ならば
振り込む可能性が減る分、二萬切りが正解となります。
　状況2
ドラ切り三面張とドラを使い切る愚形では
ドラ切り三面張が有利
　状況3
赤に祝儀がつくルールならば、
赤切り両面より赤を使い切る愚形


3.2.3　両面待ちと点数が高くなる愚形の追いかけ
上記の「両面待ちと点数2倍の愚形の追いかけ」から、
点数が2倍でないときについても結論づけられます。

まず、愚形にすると点数が2倍より大きくなるときは
愚形で追いかけるべきです。
例えば、図3.2.3のように愚形にすると
両面のときの点数の約4倍になるときは、
愚形で追いかける方が良いです。

　　ドラ
　　図3.2.3　愚形にすると点数が約4倍になる牌姿
　　　　　　　一萬切りで「リーチのみ」裏無し1300点の両面待ち
　　　　　　　四萬切りで「リーチ、三色」裏無し5200点の愚形待ち

反対に、愚形にしても点数が2倍未満のときは
両面待ちで追いかけるべきです。
例として挙げられるのは、
鳴き混一色に対々和をつけてツッパるかどうかというときです。
例えば「鳴き混一色　役牌2」の両面待ち満貫8000点にするか
「鳴き混一色　対々和　役牌2」の愚形待ち跳満12000点にするかを選べるときは、
愚形にしても点数は1.5倍にしかならず、2倍未満なので
満貫の両面待ちで全ツッパです。

　　前へ　　次へ　　目次へ

3.1 他家先制リーチでの押し引き

他家一人から先制リーチが入ったときに
自分がテンパイしたとしたら、
ツッパるべきか降りるべきかを考えます。


3.1.1　他家先制リーチ平均得点

図3.1.1は他家のリーチした手で
すべてロンしたと仮定したときの、得点分布です。
ただし、裏ドラによるハン数の増加は含めていますが、
リーチ一発であった場合は一発を含めず
また、河底やリンシャンであがった場合も
河底やリンシャンは含めない
ハン数で記録しました。



図3.1.1　先制リーチ得点分布
　約8000局の集計、主なものを図に示しました

集計した先制リーチの全得点を平均した結果、
子に放銃すると平均して5671.0点、
親に放銃すると1.5倍なので、平均8506.5点となります。
また、他家が先制リーチしたものが
すべてツモあがりしたとしたときの平均得点は、
子で7294.0点、親で10941.1点となりました。

赤なしの場合の全リーチ平均放銃得点は、
(追いかけリーチの場合も含まれて居ますが、
　先制に比べてはるかに少ないうえに
　得点分布もあまり変わりません。
　詳しくは後述)
子で5114.29点、親で7074.61点なので、[1]
赤有りの場合は多少放銃点が上がります。

なお、ブロガーが赤有りでの親の平均放銃点を求める際
子の平均放銃点を1.5倍して求めましたが、
統計による赤無しでの結果を見ると
親の点数は子の点数の1.5倍より小さいようです。
なので、ブロガーの求め方は厳密には正しくないのでしょうが
それでも大筋の話は変わらないので
とりあえず、このまま話を先に進めます。


3.1.2　他家先制リーチに対する押し引き

それでは、自分がテンパイしたときに
他家先制リーチに対し、押すか引くかを考えてみましょう。
まず、次の3パターンに状況を分けます。

1.自分が子で先制リーチ者も子
2.自分が親で先制リーチ者は子
3.自分が子で先制リーチ者は親

自分が上がる確率や放銃する確率などは
「科学する麻雀」に載っているシミュレーション結果を用います。[2]
また、先制リーチ者があがったときの得点は
先述の平均得点であるとします。
最期に自分の手の点数の大きさを変化させて、
待ちが両面待ちのときと
愚形のとき(カンチャン、シャボなど)の2つの場合について、
何点が押し引きの境界なのかを求めます。

例えば、自分も先制リーチ者も子で
自分があがればツモ、ロンに関わらず8000点だとすると
全ツッパの場合の期待値とベタオリの期待値は
図3.1.2のようになります。


図3.1.2　自分の手が8000点のときの期待値

どの巡目においても
両面も愚形も期待値がプラスで
ベタオリしたときの期待値はマイナスなので、
子の他家のリーチがあっても
自分が子で8000点の手ならツッパるべきだと言えます。

同様にして期待値を求めていくと
次のような結果が得られました。

1.自分が子で先制リーチ者も子
・追いかけリーチかベタオリか？
自分の手に裏ドラが乗る確率は
統計平均である31.74%[3]で計算します。
(以下、同様です。)
すると、
両面は全て追いかけ
愚形は、リーチのみは降りで、それ以外は追いかけ
という計算結果になりました。
ツモったときに1ハンつくことと
裏ドラが乗る可能性があることが、
追いかけたときの期待値を高くすることに
大きく寄与したようです。

・自分が鳴いているとき
両面は2000点以上で全ツッパ、それ未満はオリ
愚形は3900点以上で全ツッパ、それ未満はオリ
となりました。


2.自分が親で先制リーチ者は子
・追いかけリーチかベタオリか
両面、愚形のどちらも追いかけるべきです。

・自分が鳴いているとき
両面、愚形のどちらも全ツッパです。

ツモたれたときの親ッパネが大きいので、
ベタオリはかなり期待値が下がりました。


3.自分が子で先制リーチ者は親
・追いかけリーチかベタオリか
両面はすべて追いかけです。
愚形の場合は少し複雑で、
押すか引くかの境界は裏無しで2600点のときなのですが
裏無し2600点のときは序盤と終盤は追いかけで
中盤はベタオリという結果でした。

・鳴いているとき
両面なら2000点以上で全ツッパ、それ未満はオリ
愚形では3900点以上で全ツッパ、それ未満はオリ
となりました。


　参照
[1]ひいい　
　「近代麻雀2006年3月1日号P147　数字で語る麻雀第5回」
　　　竹書房　2006年
[2]とつげき東北　「科学する麻雀」　講談社　2004年
[3]ひいい
　「近代麻雀2006年2月15日号P136　数字で語る麻雀第4回」
　　　竹書房　2006年

　前へ　　次へ
　　　目次へ

2.1 方法

2.1.1　前提
2.1.1.1　自分と他家がテンパイかノーテンか
押し引きを論じる際、
大雑把に以下の状況に分けて考える必要があります。

自分　テンパイ　　他家　テンパイ
自分　テンパイ　　他家　ノーテン
自分　ノーテン　　他家　テンパイ
自分　ノーテン　　他家　ノーテン

以上のうち、自分と他家がテンパイしている場合以外は
赤なしと赤ありで大差がありません。
赤なしについての押し引きは既に公表されているので[1]
このブログでは、赤なしとは判断基準が異なってくるであろう
赤ありでの「自分と他家がテンパイしている場合」についてのみ扱います。

2.1.1.2　押し引きの具体的な内容
他家からはっきりとした攻撃を受けたときの対応には、
全ツッパとベタオリ、回し打ちの3種類があります。
しかし、他家の攻撃を回避しかつ自分があがる確率というのはきわめて低く
回し打ちは有効とはいえないと現在では考えられています。
よって、全ツッパとベタオリの2通りを考え、
回し打ちは考慮しません。
但し、ベタオリは100%成功するものと仮定します。


2.1.2　方法
1.他家のあがり点数を以下のあがり方に分けて記録する。
　(バイアスを避けるため、自分のあがり点数は含めていない。)

　先制リーチ
　追いかけリーチ
　面前ダマ
　喰いタンヤオ
　ドラポン
　染め手
　対々和
　以上に挙げたもの以外の鳴き手

　・ドラの種類ごとに場合分けした。

　ドラが1,9のとき
　ドラが2,8のとき
　ドラが3,7のとき
　ドラが4,6のとき
　ドラが5のとき
　ドラが三元牌のとき
　ドラが場風牌のとき
　ドラが客風牌のとき

　・親子の区別はなし
　・局による区別はなし
　・点数状況による区別はなし
　・対戦相手による区別はなし
　・データを取った場所は、
　　麻雀格闘倶楽部3,4の半荘A1リーグと
　　黄龍闘技場AAA半荘である。
　　対戦相手の質は保証されていると考えられる。
　　詳しくはこちら。
　　→戦績公開・目標設定
　・自分がゲームをしながら、対戦相手があがる度に
　　筆記であがり点数を記録した。
　・データ取得対象とした局数は、データ表示の際に付記する。

2.記録した他家のあがり点数を集計し、
　各あがり方ごとに平均点数を求める。

3.他家のあがり点数の平均と
　既に別の人のシミュレーションによって解明されている
　巡目ごとのあがり率、振込み率、ツモられ率、流局率を用いて、
　自分の手牌の点数、待ちの良さの違いごとに
　全ツッパしたときの期待値とベタオリしたときの期待値を計算し、
　押すべきか引くべきかを判断する。

　参照
[1]とつげき東北　「科学する麻雀」　講談社　2004年

　前へ　　次へ
　　　　目次へ

1.3 統計データの扱い

赤ドラ麻雀での押し引きを考察する際
統計データを用います。
ここで、統計データの取り扱いについて
補足しておきます。


1.3.1　統計データに必要なこと
麻雀戦術において統計データを用いる場合、
より多くの局についてデータを取り
その平均値を用いるという方法が一般的です。
しかし、本来平均値を用いる前提として
平均値からどの程度ゆらぐかという情報が必要です。

統計データに必要なもの
・平均値
・ゆらぎ(分散)

ゆらぎが大きい場合、より細かい条件で統計データを取らないと
人間が感覚で打牌するほうがマシになってしまう可能性があります。
(「1.3.2　具体例」を参考のこと)

ただ実際には、平均値を取るのは簡単でも
どのくらいゆらぐのかを定量化するのは
多くの場合難しいことです。
今回のデータは平均値は取りましたが、
どの位ゆらぐかは不明です。
その点を考慮したうえで、読んで下さい。
ただ、自分が何枚ドラを持っていれば
平均的な場であるかについては、後に論じようと思います。


1.3.2 具体例
統計的には「平和のみは手替わりを待つダマよりリーチ」という結果が
公表されています。[1]
しかし、例えば待ち牌が河に全て出た状況でも
「平和のみはリーチ」が正しいかというと、これは違います。
つまり、「統計的には『平和のみはリーチ』が正しい」という結論は
100回平和のみを聴牌したら、
0回リーチするよりは100回リーチする方が良いということで
100回リーチするのと90回リーチする方のどちらがよいかについては
わからないということです。


1.3.3　統計データへの反論に対する反論
　反論1
麻雀には時代ごとに打ち手のトレンドがあるので
統計データは時間が経つと使えなくなる。

　反論1への反論
時間が経ったらまたそのときにデータを取ればよい。


　反論2
麻雀は打ち手の心理や癖にも打牌は影響される。
統計データはこのような麻雀というゲームの性質を
表すことができない。

　反論2に対する反論
全くの誤り。
統計データは一般的な打ち手の心理や癖といったトレンドを
含めた情報である。
なお、当ブログが想定している不特定多数との対戦でなく、
特定の相手との対戦の場合には
統計データには特定の相手のトレンドが反映されないため
統計データが使えなくなる可能性はある。


　参照
[1]とつげき東北　「科学する麻雀」　講談社　2004年

　前へ　　　次へ
　　　　目次へ

1.2 期待値の導入

1.2.1　期待順位値の導入

麻雀は選択の連続です。
「どの牌を切るか？」
「鳴くか、鳴かないか？」
「リーチか、ダマか？」　etc
そして、より優れていると思った選択肢を
我々は選んでいくわけです。
では、「より優れている選択肢」とはどういうことでしょうか？
それは、
「ゲーム終了時に良い順位であるために最良な選択肢」
と言い換えられます。
つまり、麻雀における最良の選択肢を判断するには
ある選択肢を選んだと仮定した場合に
最終的な順位がどれくらいになるかを、
全ての選択肢について正しく把握しなければいけません。
この「最終的な順位がどれくらいになるか」を表す値を
期待順位値と呼ぶことにします。
期待順位値は以下のように定義できます。

　期待順位値
=(１×1位を取る確率)＋(2×2位を取る確率)＋(3×3位を取る確率)＋(4×4位を取る確率)　式(1.2.1.)

例えば、ゲーム開始直後で配牌を見る直前は
1位をとる確率も2位を取る確率も3位を取る確率も4位を取る確率も
全て等しく25%なので(厳密には違いますが、ここでは考慮せず。)
期待順位値は

1×0.25＋2×0.25＋3×0.25＋4×0.25＝2.5　式(1.2.2)
　よって、期待順位値　2.50位

となります。

ここで、東一局で8000点をあがったとすると、
1位や2位を取る確率が上がり、3位や4位を取る確率は下がるので
期待順位値は2.50位より良くなります。
反対に東一局で8000点を振り込むと、
1位や2位を取る確率が下がり、3位や4位を取る確率は上がるので
期待順位値は2.50位より悪くなります


1.2.2　期待順位値と他家との点数差

では、点棒移動が生じると期待順位値は
具体的にどのように変化するのでしょうか？
図1.2.1は、自分とある一人の他家との点差と
期待順位値の変化量の関係を表したグラフです。[1]


図1.2.1　ある一人の他家との点差と期待順位値の変化量の関係[1]
(他の局のグラフを知りたければ、
　引用元の「科学する麻雀」(講談社)をご覧下さい。)

例えば、東一局一本場開始時に
ある一人の他家に16000点差をつけていると、
期待順位値は2.50位から0.25位ほど良くなります。
同様に、他の二人の他家にも16000点差をつけているとしましょう。
(これは開局で4000オールをあがった場合に相当)
そうすると、他の他家に対してもそれぞれ0.25位ほど有利になるので
他家三人合計で、
　0.25×3＝0.75位分の期待順位が良くなります。


1.2.3　平場の定義と期待値

さて、ここでもう一度図1.2.1をご覧下さい。
東一局なら±20000点くらいまで
南二局なら±10000点くらいまでは、
他家一人との点差と期待順位値の変化量は
比例しているといえます。
つまり、局にもよりますが
点差が競っているときは、
他家との点差がそのまま期待順位値の変化を示す
ということができます。
これが点差が開いてしまっている状況、
例えば、南二局で18000点差の場合
大きくあがっても期待順位値はあまり向上しないことが
グラフから読み取れます。

今回、押し引きを論じるにあたっては
点差が競っていて、点差がそのまま期待順位値の
変化量を表す場合について考えていきます。
また、他家三人の点差と期待順位値の変化量が比例している状況を
平場と呼ぶことにします。　

さて、平場においては他家三人との点差の合計が
そのまま2.50位からの期待順位値の変化になるのですが、
麻雀は四人の点数の合計が常に一定であることから
他家三人との点差の合計が決定されると
一意的に自分の持ち点が決まります。
簡単なことですが、一応証明しておきます。

∵
原点をX点とする。つまり、4人の点数の合計は4X点。
ある任意の局の他家三人にリードしている分の点数差を
それぞれa点、b点、c点とおき
自分の持ち点をY点とおくと、
4人の合計点数は　4Y-(a+b+c)点。
今、4X=4Y-(a+b+c)より
　　Y=X+(1/4)(a+b+c)
ゆえに、三人との点数差の合計a+b+cが決定されると
自分の持ち点Y点が決まる。　　　　　　　　　　　　　　//

よって、平場においては
「自分の持ち点の変化が
そのまま期待順位値の変化につながる」
といえます。

ここから、平場での押すか引くかの判断はそれぞれの場合で
どの程度の持ち点の変化が見込まれるか
すなわち、それぞれの期待値を計算し
期待値が高い方を選択すればよいわけです。


　参照
[1]とつげき東北　「科学する麻雀」　講談社　2004年

　前へ　　　　次へ　　　　目次へ

1.1 麻雀での押し引き研究の歴史

麻雀において、他家の攻撃に対して押すか引くかの判断は
成績に大きな影響を与えると言われています。
ところが、押し引きの判断ははっきりとした指標がないために
個人によって判断基準がバラバラで、
かつ、よりよい押し引きとは何かがわかりづらいものです。
そこで、少しでもよりよい押し引きの追究のために
「流れ」や「対戦相手の心理を読む」といったアプローチが
取られていましたが、これらはきわめて定性的で
雀士にとって、何の役にも立たない代物でした。

このような状況に一石を投じたのが、とつげき東北さんでした。
2004年に出版した「科学する麻雀」(講談社)の中で
赤無し麻雀における押し引きについて論じています。
データやシミュレーションを用いて押し引きを定量的に論じたことは
麻雀界の歴史において大きな一歩となりました。

しかし、現在の麻雀は赤入りルールが主流となっており
赤無しに比べ他家の攻撃力が上がることから
赤無しでの場合の押し引きの判断と異なると考えられ、
赤入りでの押し引きの判断こそ知りたいという方が多いと思います。
僕が知る限り、現在赤入りでの押し引きの研究結果を公開した者はおらず、
押し引き判断を今までのように定性的な勘に頼っているのが現状です。

そこで、僕は赤入り麻雀における押し引き判断を定量的に論じるために
必要なデータを一部取ったので、
これらを元に赤入り麻雀での押し引きを考察してみました。

正直、まだまだ不備な点もあり、これからさらに調査は必要ですが
自分がわかったことを書き込んでいこうと思います。

　前へ　　次へ
　　　　目次へ