「第一打が9で以降字牌切りが続くとき、8を持っていない」
というセオリーについて検証してきました。
しかし、実際にはこのセオリーが単独で使われるのではなく
他のセオリーと複合して使われるようです。
ケース1
「2(8)を河に出している人は5を持っている可能性が高い」というセオリーと複合
他家3人が二萬を1枚ずつ捨てている。
一方、他家3人が「第一打が9筒でしばらく字牌切りが続いていて、8筒を持っていない」。
つまり、山には二-五萬が薄く、8筒が残っている。
よって、

 を残し、
を残し、 
 を嫌う
を嫌う
ケース2
「手出し5の後に手出し1は、2を固めて持っている」というセオリーとの複合
他家一人が手出し五萬の後に手出し一萬だった。
一方、他家3人が「第一打が9筒でしばらく字牌切りが続いていて、8筒を持っていない」。
つまり、山には二-五萬が薄く、8筒が残っている。
よって、

 を残し、
を残し、 
 を嫌う
を嫌う
まず、各ケースで使われたせセオリーの根拠を書きますと、
「2(8)を河に出している人は5を持っている可能性が高い」というセオリー


 と持っているときに
と持っているときに を引いた場合、
を引いた場合、
 を手牌に入れて
を手牌に入れて  を捨てるから。
を捨てるから。
(五萬を捨ててしまうと、リーチ時に八萬を勝負されてしまうため。)
「手出し5の後に手出し1は、2を固めて持っている」というセオリーとの複合



 と持っている場合、
と持っている場合、
まず手出しで を捨て、その後
を捨て、その後
 が雀頭や暗刻になるなどして
が雀頭や暗刻になるなどして  が捨てられるから。
が捨てられるから。
でも、上記に書いた根拠は100%じゃありませんよね。
「2(8)を河に出している人は5を持っている可能性が高い」というセオリーも、
5を持っていなくても、2が浮いていたら切ることはあります。
「手出し5の後に手出し1は、2を固めて持っている」というセオリーにしても


 という形なら、
という形なら、 を固めて持っているとは言えませんし、
を固めて持っているとは言えませんし、
5が1より先に切られたのは、5より1の方が安全だからなのかもしれません。
ケース1やケース2のように主張するには、
「2(8)を河に出している人は5を持っている可能性が高い」
「手出し5の後に手出し1は、2を固めて持っている」
といったことを定量化しなければいけません。
例えば、「2を河に出している人は、5を平均1.3枚持っている」とわかれば
「第一打が9で以降字牌切りが続くとき、8を持っていない」の
計算結果と照らし合わせて、比較することができます。
「2を河に出している人は、平均して何枚5を持っているか?」や
「手出し5の後に手出し1の場合は、平均して何枚2を持っているか?」は
ネット上に落ちている東風荘の牌譜を、
CPUで検索してやればわかる可能性があります。
僕個人としても、有効なコード記述を思いつけば
やってみたいと考えています。
とにかく、現時点ではケース1やケース2が正しいかを
判別することができません。
問題なのは、定量化しないとわからないことを
さもわかっているかのように言う麻雀界です。
定量化の進んでない分野では
魑魅魍魎な世界になり、でたらめが飛び交うのが常ですが、
麻雀界は特にひどいと思います。
「有名な人が言うから正しいのだろう。」という
態度は改めなければいけません。
自分で検証する習慣が大切だと思います。
まとめ
「第一打が9で以降字牌切りが続くとき、8を持っていない」というセオリーと
他のセオリーを複合するならば、
他のセオリーも完全に定量化されなければいけない。
最後に
今まで、「他家3人が持っていない」という場合に関して議論してきましたが
「他家2人が持っていない(もう1人は持っているか不明)」
「他家1人が持っていない(もう2人は持っているか不明)」
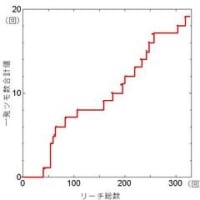
の場合についての計算結果を、図1-1に示します。

図1-1 ツモる確率の「持っていない他家の人数」依存性
枚数が多いほど、何人の他家が持っていないかが効いてきます。
また、1人不持程度では、たいして確率が変動しないのがわかります。
やはり、ツモ山を気にするくらいなら
自分の手牌を見て、三色などを見逃さないよう注意した方がよいでしょう。
前へ 次へ
目次へ
というセオリーについて検証してきました。
しかし、実際にはこのセオリーが単独で使われるのではなく
他のセオリーと複合して使われるようです。
ケース1
「2(8)を河に出している人は5を持っている可能性が高い」というセオリーと複合
他家3人が二萬を1枚ずつ捨てている。
一方、他家3人が「第一打が9筒でしばらく字牌切りが続いていて、8筒を持っていない」。
つまり、山には二-五萬が薄く、8筒が残っている。
よって、

 を残し、
を残し、 
 を嫌う
を嫌うケース2
「手出し5の後に手出し1は、2を固めて持っている」というセオリーとの複合
他家一人が手出し五萬の後に手出し一萬だった。
一方、他家3人が「第一打が9筒でしばらく字牌切りが続いていて、8筒を持っていない」。
つまり、山には二-五萬が薄く、8筒が残っている。
よって、

 を残し、
を残し、 
 を嫌う
を嫌うまず、各ケースで使われたせセオリーの根拠を書きますと、
「2(8)を河に出している人は5を持っている可能性が高い」というセオリー


 と持っているときに
と持っているときに を引いた場合、
を引いた場合、 を手牌に入れて
を手牌に入れて  を捨てるから。
を捨てるから。(五萬を捨ててしまうと、リーチ時に八萬を勝負されてしまうため。)
「手出し5の後に手出し1は、2を固めて持っている」というセオリーとの複合



 と持っている場合、
と持っている場合、まず手出しで
 を捨て、その後
を捨て、その後
 が雀頭や暗刻になるなどして
が雀頭や暗刻になるなどして  が捨てられるから。
が捨てられるから。でも、上記に書いた根拠は100%じゃありませんよね。
「2(8)を河に出している人は5を持っている可能性が高い」というセオリーも、
5を持っていなくても、2が浮いていたら切ることはあります。
「手出し5の後に手出し1は、2を固めて持っている」というセオリーにしても


 という形なら、
という形なら、 を固めて持っているとは言えませんし、
を固めて持っているとは言えませんし、5が1より先に切られたのは、5より1の方が安全だからなのかもしれません。
ケース1やケース2のように主張するには、
「2(8)を河に出している人は5を持っている可能性が高い」
「手出し5の後に手出し1は、2を固めて持っている」
といったことを定量化しなければいけません。
例えば、「2を河に出している人は、5を平均1.3枚持っている」とわかれば
「第一打が9で以降字牌切りが続くとき、8を持っていない」の
計算結果と照らし合わせて、比較することができます。
「2を河に出している人は、平均して何枚5を持っているか?」や
「手出し5の後に手出し1の場合は、平均して何枚2を持っているか?」は
ネット上に落ちている東風荘の牌譜を、
CPUで検索してやればわかる可能性があります。
僕個人としても、有効なコード記述を思いつけば
やってみたいと考えています。
とにかく、現時点ではケース1やケース2が正しいかを
判別することができません。
問題なのは、定量化しないとわからないことを
さもわかっているかのように言う麻雀界です。
定量化の進んでない分野では
魑魅魍魎な世界になり、でたらめが飛び交うのが常ですが、
麻雀界は特にひどいと思います。
「有名な人が言うから正しいのだろう。」という
態度は改めなければいけません。
自分で検証する習慣が大切だと思います。
まとめ
「第一打が9で以降字牌切りが続くとき、8を持っていない」というセオリーと
他のセオリーを複合するならば、
他のセオリーも完全に定量化されなければいけない。
最後に
今まで、「他家3人が持っていない」という場合に関して議論してきましたが
「他家2人が持っていない(もう1人は持っているか不明)」
「他家1人が持っていない(もう2人は持っているか不明)」
の場合についての計算結果を、図1-1に示します。

図1-1 ツモる確率の「持っていない他家の人数」依存性
枚数が多いほど、何人の他家が持っていないかが効いてきます。
また、1人不持程度では、たいして確率が変動しないのがわかります。
やはり、ツモ山を気にするくらいなら
自分の手牌を見て、三色などを見逃さないよう注意した方がよいでしょう。
前へ 次へ
目次へ



















またブログ頑張ってください。
今日もブログ頑張ってください。
体調はどうですか??
ムリせずお仕事頑張ってくださいね!
応援してます。
ブログ頑張ってくださいね。
応援していますね。