高機能自閉症の子に「教えて」と助けを求めて教える力をつけていくべき? 2
の続きです。
高機能自閉症の子だけでなくアスペルガー症候群やグレーゾーンの子も含めて
自閉症スペクトラムの子にどうすればじっくり考えることを身につける
手助けができるのか、わたしが関わった子らとの体験に基づいて説明しますね。
このタイプの子でも、熟考できる範囲が限定されているのですが(その子が好む分野の好む部分)
熟考ができる子がいます。
論理的に筋道を立てて考えを追っていくことができるのです。
もともとIQが高めで、算数や数学、理科といった学習に『こだわり』を
持っているように見える子です。
数理パズルがすごく好きだったり、プラモデルの組み立てなどが好きだったりすると、
そうした知的な遊びへの執着が、学習の場面への思考につながることはよくあります。
また幼児期の数の敏感期に見られるような
秩序に基づいて、規則性のある物の並べ方を好んだり、数にこだわったりする姿が
幼児期を超えて小学校に入っても遊びの中で何度も再現される場合、
それがじっくり思考する力の基盤となっていくのもよく見ます。
見たところ、とても幼い遊びのように感じられても、そうした遊びに没頭する時間を
十分与えてあげることが大事なのだと思います。
ただこうした子も、他人から学ぶのが苦手だったり、好きな分野以外の常識的な判断が危かったり、
わからない時に即座に切り捨てる癖がついていたりすると、
問題が自分好みのものでなくなったり、難易度が上がってお手上げになると、
思考を続けていくのが難しくなります。
そのための対応を、発達障がいはあるけれど学校の成績は良い子の注意点と伸ばし方 1
発達障がいはあるけれど学校の成績は良い子の注意点と伸ばし方 2 に書きました。(また次回にこれについて
もう少しくわしく書く予定)
発達障がいがある子は、たいてい、「目に見えない」イメージを扱うことが苦手です。
(もっともADHDの子のなかには、抽象概念等がとても得意な子もいると思います。また
アスペルガー症候群の子の中で言葉の世界にこだわる子の場合、抽象的な言葉を取り扱う熟考を好む子もいると思います。)
特に苦手なのは、人の心が判断するあいまいな「目に見えない」イメージです。
次に紹介するのは、アスペルガー症候群の子に3ケタ÷2ケタの計算を教えているところです。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
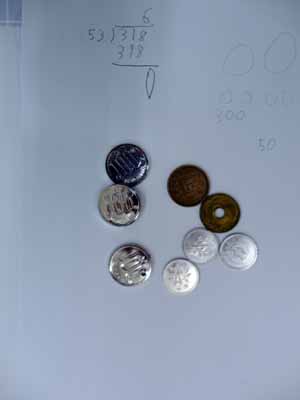
4年生の☆ちゃんのレッスンです。
3ケタ÷2ケタの計算で、少し困惑している模様。
お金を使って、だいたいこれくらいの数で割れるかな~という
おおよその数を設定する練習をしています。
アスペルガー症候群の☆ちゃんは、
「318円がだいたい300円くらいで、
こういうものが買えそうだ」という日常で把握している数の感性が
無に等しいです。
「312円が318円になっても、たいしてうれしくないけど、
312円が381円になるのなら、
50円1枚分は得しているな」とピンとくる感性です。
そのため、割り算のケタ数が増えてくると、
混乱することが多くなってきたのです。
☆ちゃんに、「割られる数の上から2つの数と、2ケタの割る数見比べて、
割れなかったら、3つめの数も入れて、とりあえず最初の数だけ残して後を0にして、
5×1=5 5×2=10 としていけば解けるのよ」
と手順だけを訓練していって
できるようにさせることは可能なのです。
そのように、学校で学んできた算数は
意味がわからないまま丸暗記を積み重ねて、
これまできているのです。
このまま、電話番号を暗記するように
形だけ暗記してできるようになっていく危険を感じて、
根本的な数の感性の弱さを克服する形の
アプローチも大事だと感じています。
◆ お金を見た時に、だいたいがわかる感性、
(「325円って、だいたい何百円なのか。
389円て、だいたい何百円なのか。
82円あるとき、20円のガムがいくつ買えるのかなど)
◆ 指1本を10円として、9の指を90円と考え、
目で手を見ながら、90÷30ができる感性
などを育てていくことが大事だと考えています。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
自閉症スペクトラムの子たちの学習を見ていると、
計算はできるようになっている場合でも、ルールを形式的に覚えているだけで
極端なほどに意味を把握していないことがよくあります。
たとえば分数の計算がかなり複雑なものまで解けるようになっている時でも、
「3分の1を3つ足すと1になるね。」と1つのカステラを3等分して見せて、
それを見せながら、「どうして3つに切ったものを3つ合わせると1になるんだろう?」といった質問をすると、
「わからない」と言う、といった具合です。
先に計算等でできていることに関して、意味としてわからせるために
具体物を使って理解度を確かめようとすると、
「あっそうか」と腑に落ちるのではなくて、
計算の世界とは全く異物を見るように心そこにあらずで、「知らない」と言ったり、
めちゃくちゃな答えを言い続けたり、「わからないわからない」と大騒ぎしたりすることがあります。
小数点の計算がしっかりできる子に、ものさしの1mmの目盛を指して、
「何センチに当たると思う?小数点を使って、言える?」とたずねると、
キョトンとしていたりするのです。
次回に続きます。



















