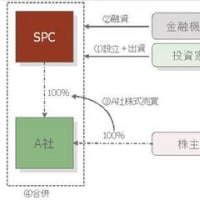
ケース①「新規事業に参入して、企業のビジネスリスクが変化するとき」
アンレバードβは、非上場企業のβを求めるときだけでなく、ある企業が新規事業に参入する際、あるいは新規事業を買収する際のビジネスリスクを求めるときにも用いられます。
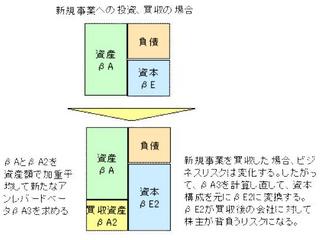
企業の事業構成を変える場合、それまでのβで表されるリスクだけを考えるのは不十分で、新規事業のリスクを企業のリスクとして織り込む必要があります。そこで「新規事業のビジネスだけのリスクを表すアンレバードβ」を「業界他社のアンレバードβ」を参考に算出して、「企業の新規事業を加える前のアンレバードβ」と資産額ベースで加重平均します。
そこで、求めたアンレバードβは、自社の資本構成に応じてレバードβに変換してその企業のβとして扱います。
ケース②「事業部ごとのリスクを求めるとき」
同じ企業の中でも、競争環境が全く異なる事業が複数ある場合、全社のβを用いると投資の判断を誤ってしまいます。そこで事業部ごとにβを求めることがあります。その際にも業界他社を参考にアンレバードβを求めます。

○ アンレバードβ計算式の導出
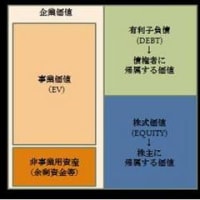
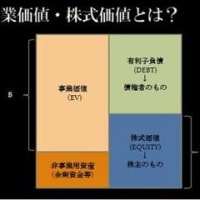
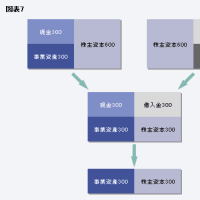
アンレバードβの導出は、B/Sから考えてきます。次のように調達側の負債Dと資本Eが、負債の節税効果と無借金とした場合の資産に分かれていたとします。

(βはそれぞれのリスクを、tは実効税率を示します)
このとき、各βは次のように求められます。
(D+E-t×D)×βu+(t×D)×βD/(D+E-t×D)+(t×D)
=(D×βD)+(E×βL)/(D+E)
βL=βL×1+(1-t)D/E-βD×(1-t)D/E
このとき負債に対するリスクβDはマーケットリスクに対して変動がほとんどないと考えられるので、ゼロと見なすことができます。このとき、上の式を変形するとβuとβLの関係は次のようになります。
βu=βL/〔1+(1-t)D/E〕
○ アンレバードβ計算式の意味
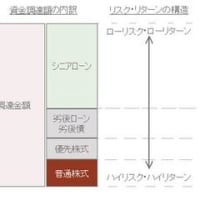
アンレバードβ、レバードβ計算式は、負債の額が大きい時の方が、株主から見たリスク(レバードβ=βL)が大きくなることを示しています。これは、最も安全なCFは債権者に流れるので、債権者への負債が大きければ大きいほど、株主向けに確保されるCFがより大きな危険にさらされるということに整合しているといえます。
アンレバードβは、非上場企業のβを求めるときだけでなく、ある企業が新規事業に参入する際、あるいは新規事業を買収する際のビジネスリスクを求めるときにも用いられます。
企業の事業構成を変える場合、それまでのβで表されるリスクだけを考えるのは不十分で、新規事業のリスクを企業のリスクとして織り込む必要があります。そこで「新規事業のビジネスだけのリスクを表すアンレバードβ」を「業界他社のアンレバードβ」を参考に算出して、「企業の新規事業を加える前のアンレバードβ」と資産額ベースで加重平均します。
そこで、求めたアンレバードβは、自社の資本構成に応じてレバードβに変換してその企業のβとして扱います。

ケース②「事業部ごとのリスクを求めるとき」
同じ企業の中でも、競争環境が全く異なる事業が複数ある場合、全社のβを用いると投資の判断を誤ってしまいます。そこで事業部ごとにβを求めることがあります。その際にも業界他社を参考にアンレバードβを求めます。

○ アンレバードβ計算式の導出
アンレバードβの導出は、B/Sから考えてきます。次のように調達側の負債Dと資本Eが、負債の節税効果と無借金とした場合の資産に分かれていたとします。

(βはそれぞれのリスクを、tは実効税率を示します)
このとき、各βは次のように求められます。
(D+E-t×D)×βu+(t×D)×βD/(D+E-t×D)+(t×D)
=(D×βD)+(E×βL)/(D+E)
βL=βL×1+(1-t)D/E-βD×(1-t)D/E
このとき負債に対するリスクβDはマーケットリスクに対して変動がほとんどないと考えられるので、ゼロと見なすことができます。このとき、上の式を変形するとβuとβLの関係は次のようになります。
βu=βL/〔1+(1-t)D/E〕
○ アンレバードβ計算式の意味
アンレバードβ、レバードβ計算式は、負債の額が大きい時の方が、株主から見たリスク(レバードβ=βL)が大きくなることを示しています。これは、最も安全なCFは債権者に流れるので、債権者への負債が大きければ大きいほど、株主向けに確保されるCFがより大きな危険にさらされるということに整合しているといえます。