p-n接合とは
Bなどが注入されたp型の半導体とAs、Pが注入されたn型の半導体をつなげたものをp-n接合という。
p-n接合の最も重要な特性は整流性である。下図参照

順バイアス:p側に正電圧をかけていくと電圧の増加と主に電流が急速に増加する。逆バイアス:一方、逆方向に電圧をかけていくと電流はほとんど流れないが臨界電圧に達すると降伏して電流が流れる。逆方向の降伏電圧は接合の濃度差などのパラメータに依存する。
p-nの接合によってキャリアの拡散が起こる。p→nは正孔が、n→pは電子が拡散する。p側からは正孔が移動し負のアクセプタイオンは格子に補足されているために取り残される。一方、n側からは電子が移動し、正のドナーが取り残される。
p側は負、n側は正に帯電する。この空間電化によってn→pの電界が発生して電界によるドリフト電流が拡散電流とは反対方向に流れる。
熱平衡の状態においては電流はゼロであり前述の拡散電流とドリフト電流はつりあっている。この場合フェルミ準位は資料の全体にわたって一定である。それぞれのキャリアは拡散しあって中心部でキャリアのない空乏層が出来る。

内蔵電位
熱平衡状態におけるp型とn型の領域の電位差を内蔵電位(built-in-potential)といって
Vbi=ΨnーΨp=kT/q・ln(NaNd/ni^2)であらわされる。
p-n接合の空乏領域ではキャリアが存在せずアクセプタ、ドナーイオンのみになる。実際には遷移領域があるがSi GaAsでは遷移領域が狭いのでほとんど無視できる。

空乏層
空乏領域は不純物注入が浅い場合の階段接合、深い場合の傾斜接合と二つに近似して考えることが出来る。それぞれの場合においてポアソン方程式、正味の空間電荷がゼロであるという条件を考慮してやると空乏層幅が求まる。
幅 W=√[2ε/q・(Na+Nd)/NaNd・Vbi]
電界を考えるとVbiはちょうど面積になる。
これより不純物濃度の差が大きいほど内蔵電位もあがるので空乏層が広がることが分かる。
片側の不純物濃度がずっと大きい場合(たとえばNa≫Nd)にはp型の空乏層が非常に狭くなりn型の空乏層のみが存在すると考えてよい。
幅 W=√[2ε・Vbi/(q・Nd)]
外部電圧の影響
外部電圧を書けた場合を下図のように考える。

pに+電界が加えられるとVbiにマイナスされた形になるので
空乏層幅は狭くなりポテンシャル障壁が減るので電子、正孔は移動しやすくなり電流が流れる。一方で逆バイアスの場合は障壁があがり空乏層も広がるので電子は移動しにくくなり電流は流れない。
Vの電圧を加えた時の空乏層幅は
幅 W=√[2ε・(Vbi-V)/(q・Nd)]
Vは順方向の場合に正
傾斜接合

傾斜接合による内蔵電位、空乏層幅は
Vbi=q・a・W^3/12εs
W=[12εs・Vbi/(q/a)]^(1/3)
となって印加電圧に対して(V) ^(1/3)
で反応するので空乏層の伸びが抑えられ、微細化したトランジスタではわざと傾斜接合を狙う場合もある。
空乏層容量
空乏層容量は電圧印加による電荷の変化分C=dQ/dVであらわされる。
単位面積あたりの空乏層容量は
Cj=εs/Wである。
面積Sを考えるとC=εs・S/dである。
これは平行平板のコンデンサーの容量と同じでありこの仮定は逆方向バイアスの場合は成り立つ。順方向バイアスの場合は大きな電流が接合部を流れ空乏層内に多数のキャリアが注入されるために拡散容量が生じる。
Nbを不純物濃度として
Cj=εs/W=√{q・εs・Nb/[2・(Vbi-V)]}
つまり1/Cj^2 =2・(Vbi-V)/(q・εs・Nb)
でありVと1/Cj^2をプロットしていけば傾きから不純物濃度、切片からVbiが分かる。
電流電圧特性
p-n接合に電圧を印加すると拡散電流とドリフト電流の均衡が破れる。順方向バイアスの場合は空乏領域が減少するためにドリフト電流は拡散電流に比べて少なくなる。これによりキャリアが移動して電流が流れる。
逆方向バイアスでは空乏領域が増大し静電ポテンシャルが増加するために拡散電流が減少する。
ダイオードの理想特性を考える際に仮定を行う。
(a)階段状の空乏領域を持ち境界の外側は中性
(b)境界の外側のキャリア濃度は接合両側の静電ポテンシャルの差で表される
(c)注入された少数キャリアの密度は多数キャリアよりも少ない
(d)空乏領域での生成、再結合は生じておらず電流は一定である。
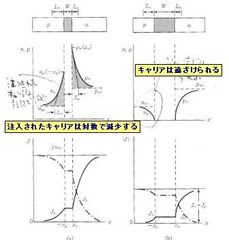
順方向バイアス、逆方向バイアスにおける少数キャリアの密度分布と電流の様子をした図に示している。
キャリア数(電子であればN、正孔であればP)に添え字n,pをつけて半導体の型を示す。さらに0は熱平衡時の密度である。

p-n接合の内蔵電位Vbiは
Vbi=kT/qln(Pp0・Nn0/ni^2)=kT/qln(Nn0/Np0) ∵ni^2=Pp0・Np0
これを変形して
Nn0=Np0・exp(qVbi/kT)
となって熱平衡下ではVbiによって境界のキャリア密度が表示されることが分かる。
少数キャリアについては
Np=Np0exp(qV/kT)であり注入された少数キャリアは対数で減少していくことが上図からもわかる。これは多数キャリアとの再結合によるものである。
逆バイアスの場合はVがマイナスなので逆に少数キャリアが遠ざけられる分布になっており電流はほとんど流れない。
実際のSiのデバイスでは空乏領域においてのキャリアの生成再結合が起こっておりこれによる電流は無視できない。生成、再結合割合は真性フェルミ準位の近傍にある生成中心のみが生成割合に大事な役割をする。
逆バイアスの場合はキャリアが不足するので生成電流、順バイアスの場合はむしろキャリアがあまるので再結合電流を考慮する必要がある。

電荷の蓄積と過渡特性
n型領域に注入された少数キャリア=正孔の蓄積電荷は
Qp=Lp^2/DpJp(xn)=τpJp(xn)となる。
Lp=√(Dp・τp)は拡散長、Dpは拡散係数、τはキャリア寿命である
蓄積電荷はキャリア寿命と電流の積で表されることを示している。
これは注入された正孔の寿命が長いほど再結合する前に内部に拡散して蓄積されるためである。
順バイアスの際には接合の空乏領域の容量に加えて蓄積電荷の分を接合容量に加える必要がある。
拡散容量 Cd=A・q^2・Lp・Pp0/kT・exp(qV/kT)
Aは接合の断面積である。
p-n接合の等価回路は下図のようにになる。

接合、拡散容量分に加えてp-n接合で流れる電流はコンダクタンスとして加える必要があり
G=A・dJ/dV=qA/kT・Js・exp(qV/kT)=qA/kT(J+Js)≒qI/kT
と表すことが出来る。
スイッチングにp-n接合を用いる際は過渡応答を考える必要がある。
下図のような回路を考える。

t=0でスイッチが右に倒されると初期の逆方向電流Ir=V/Rが流れる。過渡応答時間toffは電流が最初の逆方向電流Irの10パーセントになる時間である。
蓄積少数キャリアは
Qp=τp・Jp=τp・If/A Ifは順方向電流、Aはデバイス面積である。
スイッチング時間中の平均電流をIr_aveとすると
スイッチング時間は前キャリアを吐き出すのに要する時間であり、
toff=QpA/Ir_ave=τp(If/Ir_ave)となる
したがってオフ時間はキャリア寿命に依存する。
このことから高速なデバイスを作るためにはバンドギャップ中央に準位を持つAuのような再結合中心が用いられる。
接合の降伏
p-n接合に大きな逆方向電圧が印加されると降伏現象を起こして大電流が流れる。
降伏現象の機構としては酸化膜の回でも述べたトンネル効果となだれ降伏がある。

トンネリングは価電子帯から導電帯に直接キャリアが遷移する現象で1MV/cm以上の電界が必要である。このような高電界を得るためにはp領域、n領域における不純物濃度を十分高く取らなくてはいけない(5e17cm-3以上)。降伏電圧が4Eg/q以下の場合はトンネル現象であるといえる。
なだれ増倍過程エネルギーを得た電子が電界からエネルギーを受け取って電子ー正孔対を生成する過程が連続して起こる現象である。
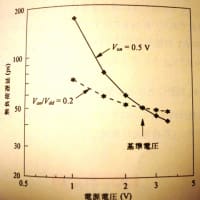
降伏時の臨界電界強度Eを不純物濃度に対してプロットしたものが下図である。

高濃度の時のみトンネル仮定で降伏する。
通常のp-n接合の降伏はなだれ過程で律速される。
片側階段接合での降伏電圧は
Vb=EcW/2=εsE^2/2=εsE^2/(2q)・Nb^(-1)
Nbは低ドーピング側の不純物濃度である。
傾斜接合の場合は
Vb=2EcW/3=4/3・E^(3/2)・(2εs/q)^(1/2)・a^(-1/2)
aは不純物の勾配である。
降伏電圧は階段接合ではNb^-1 傾斜接合ではa^-1/2で変化する。

Bなどが注入されたp型の半導体とAs、Pが注入されたn型の半導体をつなげたものをp-n接合という。
p-n接合の最も重要な特性は整流性である。下図参照
順バイアス:p側に正電圧をかけていくと電圧の増加と主に電流が急速に増加する。逆バイアス:一方、逆方向に電圧をかけていくと電流はほとんど流れないが臨界電圧に達すると降伏して電流が流れる。逆方向の降伏電圧は接合の濃度差などのパラメータに依存する。
p-nの接合によってキャリアの拡散が起こる。p→nは正孔が、n→pは電子が拡散する。p側からは正孔が移動し負のアクセプタイオンは格子に補足されているために取り残される。一方、n側からは電子が移動し、正のドナーが取り残される。
p側は負、n側は正に帯電する。この空間電化によってn→pの電界が発生して電界によるドリフト電流が拡散電流とは反対方向に流れる。
熱平衡の状態においては電流はゼロであり前述の拡散電流とドリフト電流はつりあっている。この場合フェルミ準位は資料の全体にわたって一定である。それぞれのキャリアは拡散しあって中心部でキャリアのない空乏層が出来る。
内蔵電位
熱平衡状態におけるp型とn型の領域の電位差を内蔵電位(built-in-potential)といって
Vbi=ΨnーΨp=kT/q・ln(NaNd/ni^2)であらわされる。
p-n接合の空乏領域ではキャリアが存在せずアクセプタ、ドナーイオンのみになる。実際には遷移領域があるがSi GaAsでは遷移領域が狭いのでほとんど無視できる。
空乏層
空乏領域は不純物注入が浅い場合の階段接合、深い場合の傾斜接合と二つに近似して考えることが出来る。それぞれの場合においてポアソン方程式、正味の空間電荷がゼロであるという条件を考慮してやると空乏層幅が求まる。
幅 W=√[2ε/q・(Na+Nd)/NaNd・Vbi]
電界を考えるとVbiはちょうど面積になる。
これより不純物濃度の差が大きいほど内蔵電位もあがるので空乏層が広がることが分かる。
片側の不純物濃度がずっと大きい場合(たとえばNa≫Nd)にはp型の空乏層が非常に狭くなりn型の空乏層のみが存在すると考えてよい。
幅 W=√[2ε・Vbi/(q・Nd)]
外部電圧の影響
外部電圧を書けた場合を下図のように考える。
pに+電界が加えられるとVbiにマイナスされた形になるので
空乏層幅は狭くなりポテンシャル障壁が減るので電子、正孔は移動しやすくなり電流が流れる。一方で逆バイアスの場合は障壁があがり空乏層も広がるので電子は移動しにくくなり電流は流れない。
Vの電圧を加えた時の空乏層幅は
幅 W=√[2ε・(Vbi-V)/(q・Nd)]
Vは順方向の場合に正
傾斜接合
傾斜接合による内蔵電位、空乏層幅は
Vbi=q・a・W^3/12εs
W=[12εs・Vbi/(q/a)]^(1/3)
となって印加電圧に対して(V) ^(1/3)
で反応するので空乏層の伸びが抑えられ、微細化したトランジスタではわざと傾斜接合を狙う場合もある。
空乏層容量
空乏層容量は電圧印加による電荷の変化分C=dQ/dVであらわされる。
単位面積あたりの空乏層容量は
Cj=εs/Wである。
面積Sを考えるとC=εs・S/dである。
これは平行平板のコンデンサーの容量と同じでありこの仮定は逆方向バイアスの場合は成り立つ。順方向バイアスの場合は大きな電流が接合部を流れ空乏層内に多数のキャリアが注入されるために拡散容量が生じる。
Nbを不純物濃度として
Cj=εs/W=√{q・εs・Nb/[2・(Vbi-V)]}
つまり1/Cj^2 =2・(Vbi-V)/(q・εs・Nb)
でありVと1/Cj^2をプロットしていけば傾きから不純物濃度、切片からVbiが分かる。
電流電圧特性
p-n接合に電圧を印加すると拡散電流とドリフト電流の均衡が破れる。順方向バイアスの場合は空乏領域が減少するためにドリフト電流は拡散電流に比べて少なくなる。これによりキャリアが移動して電流が流れる。
逆方向バイアスでは空乏領域が増大し静電ポテンシャルが増加するために拡散電流が減少する。
ダイオードの理想特性を考える際に仮定を行う。
(a)階段状の空乏領域を持ち境界の外側は中性
(b)境界の外側のキャリア濃度は接合両側の静電ポテンシャルの差で表される
(c)注入された少数キャリアの密度は多数キャリアよりも少ない
(d)空乏領域での生成、再結合は生じておらず電流は一定である。
順方向バイアス、逆方向バイアスにおける少数キャリアの密度分布と電流の様子をした図に示している。
キャリア数(電子であればN、正孔であればP)に添え字n,pをつけて半導体の型を示す。さらに0は熱平衡時の密度である。
p-n接合の内蔵電位Vbiは
Vbi=kT/qln(Pp0・Nn0/ni^2)=kT/qln(Nn0/Np0) ∵ni^2=Pp0・Np0
これを変形して
Nn0=Np0・exp(qVbi/kT)
となって熱平衡下ではVbiによって境界のキャリア密度が表示されることが分かる。
少数キャリアについては
Np=Np0exp(qV/kT)であり注入された少数キャリアは対数で減少していくことが上図からもわかる。これは多数キャリアとの再結合によるものである。
逆バイアスの場合はVがマイナスなので逆に少数キャリアが遠ざけられる分布になっており電流はほとんど流れない。
実際のSiのデバイスでは空乏領域においてのキャリアの生成再結合が起こっておりこれによる電流は無視できない。生成、再結合割合は真性フェルミ準位の近傍にある生成中心のみが生成割合に大事な役割をする。
逆バイアスの場合はキャリアが不足するので生成電流、順バイアスの場合はむしろキャリアがあまるので再結合電流を考慮する必要がある。
電荷の蓄積と過渡特性
n型領域に注入された少数キャリア=正孔の蓄積電荷は
Qp=Lp^2/DpJp(xn)=τpJp(xn)となる。
Lp=√(Dp・τp)は拡散長、Dpは拡散係数、τはキャリア寿命である
蓄積電荷はキャリア寿命と電流の積で表されることを示している。
これは注入された正孔の寿命が長いほど再結合する前に内部に拡散して蓄積されるためである。
順バイアスの際には接合の空乏領域の容量に加えて蓄積電荷の分を接合容量に加える必要がある。
拡散容量 Cd=A・q^2・Lp・Pp0/kT・exp(qV/kT)
Aは接合の断面積である。
p-n接合の等価回路は下図のようにになる。
接合、拡散容量分に加えてp-n接合で流れる電流はコンダクタンスとして加える必要があり
G=A・dJ/dV=qA/kT・Js・exp(qV/kT)=qA/kT(J+Js)≒qI/kT
と表すことが出来る。
スイッチングにp-n接合を用いる際は過渡応答を考える必要がある。
下図のような回路を考える。
t=0でスイッチが右に倒されると初期の逆方向電流Ir=V/Rが流れる。過渡応答時間toffは電流が最初の逆方向電流Irの10パーセントになる時間である。
蓄積少数キャリアは
Qp=τp・Jp=τp・If/A Ifは順方向電流、Aはデバイス面積である。
スイッチング時間中の平均電流をIr_aveとすると
スイッチング時間は前キャリアを吐き出すのに要する時間であり、
toff=QpA/Ir_ave=τp(If/Ir_ave)となる
したがってオフ時間はキャリア寿命に依存する。
このことから高速なデバイスを作るためにはバンドギャップ中央に準位を持つAuのような再結合中心が用いられる。
接合の降伏
p-n接合に大きな逆方向電圧が印加されると降伏現象を起こして大電流が流れる。
降伏現象の機構としては酸化膜の回でも述べたトンネル効果となだれ降伏がある。
トンネリングは価電子帯から導電帯に直接キャリアが遷移する現象で1MV/cm以上の電界が必要である。このような高電界を得るためにはp領域、n領域における不純物濃度を十分高く取らなくてはいけない(5e17cm-3以上)。降伏電圧が4Eg/q以下の場合はトンネル現象であるといえる。
なだれ増倍過程エネルギーを得た電子が電界からエネルギーを受け取って電子ー正孔対を生成する過程が連続して起こる現象である。
降伏時の臨界電界強度Eを不純物濃度に対してプロットしたものが下図である。
高濃度の時のみトンネル仮定で降伏する。
通常のp-n接合の降伏はなだれ過程で律速される。
片側階段接合での降伏電圧は
Vb=EcW/2=εsE^2/2=εsE^2/(2q)・Nb^(-1)
Nbは低ドーピング側の不純物濃度である。
傾斜接合の場合は
Vb=2EcW/3=4/3・E^(3/2)・(2εs/q)^(1/2)・a^(-1/2)
aは不純物の勾配である。
降伏電圧は階段接合ではNb^-1 傾斜接合ではa^-1/2で変化する。