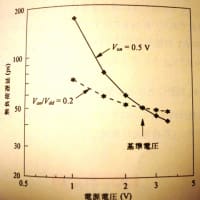
電源電圧が同じであればCMOSデバイスの遅延はデバイスの電流とスイッチングの容量で決定される。
ソース・ドレイン抵抗
特にソース側の抵抗はゲートのドライブ電圧を減らす役割をするので問題となる。

図はS/D領域における電流の流れを示したものである。S/D抵抗は
Rac G-S、G-Dのオーバーラップ部の蓄積層抵抗
Rsp 表面層からS/Dの深さまで電流が流れる部分の抵抗
Rsh 電流が均一に流れている部分の抵抗
Rco 電流がコンタクト部分に流れ込む領域のコンタクト抵抗
コンタクトのメタル部分は非常に抵抗は低くなるので
Alの場合 0.05Ω/□ ⇔ チャネルシート抵抗 2000~7000Ω/□
Rcoはほとんど無視できる。
蓄積層抵抗Racはゲート電圧に依存し、Racは実効チャネル長Leffの一部だとして考えることが出来る。

Rspは図のような電流の広がりが均一にDopeされた抵抗体の中で生じるとの仮定の下に求められている。
Rsp=2ρ/(π・W)・ln(0.75・xj/xc)
ここでWはデバイス幅、xjは接合深さ、xcは反転層厚さである。
典型的なxj/xc≒40と言う値に対しRsp≒2・ρ/Wが得られる。
しかしながら実際には電流の広がりは横方向の不純物勾配により局所的に抵抗率が均一で無い領域で起こるため詳細な解析はSimulationをする必要がある。一般的にはRac+Rspの和が最小になるように電流が流れる。
急峻なS/D不純物Profileを作った場合はRac、Rspは共に低くLeff=Lmetである。
一方で勾配の緩やかなProfileの場合にはRac、Rspが大きくなりLeff>Lmetである。
S/D拡散層のシート抵抗は
Rsh=ρsd・S/W
ρsdはS/Dの抵抗率、Wはデバイス幅、Sはゲート端とコンタクト端との距離
ρsdは50-500Ω/□の値が一般的である。Sはゲート幅に合わせてなるべく多くのコンタクトを配置することによって小さく出来る。
コンタクト抵抗
Rco=√(ρsd・ρc)/W・coth(lc・√(ρsd/ρc))
ρcはコンタクト部分の抵抗率、lcはコンタクト開口幅である。
Rcoにはコンタクト直下の電流集中による抵抗が含まれる。
拡散層のシリサイド化が行われていない場合、コンタクトの大きさにより長コンタクトと短コンタクトの極限を持つ。
短コンタクトは抵抗がコンタクト幅に依存する場合であり
Rco=ρc/(W・lc)
長コンタクトの場合は電流はコンタクトのゲート側に流れ込むためlcに依存しない
Rco=√(ρsd・ρc)/W
金属⇔高濃度Dopeシリコン間のオーミックコンタクトでは伝道電流がトンネリング、電界放出に支配される。コンタクト抵抗は障壁高さψBと表面濃度Ndに指数関数的に依存する。
ρc ∝ exp(4πψB/qh・√(m*・εsi/Nd))
hはプランク定数、m*は有効質量である

サリサイド技術を用いた場合はS/Dの抵抗よりも大幅にサリサイド部分の抵抗が低くなるのですべての電流が引き込まれスペーサ下部の抵抗のみが貢献する。
また拡散層全体がコンタクト領域になるので拡散層幅d=コンタクト幅lcになり長コンタクトの極限が適用できる。一方でS/Dの拡散層抵抗はシリサイドで高濃度層が消費されるために高くなることに注意する必要がある。
寄生容量

MOSFETには真性の容量成分:Cg、Cdに加えて寄生容量が存在する。
S/D拡散層⇔基板の接合容量、Gate-S/D領域のOverLap容量が挙げられる
S/Dと基板は反対の導電性にドーピングされているので接合拡散層容量が生じる。
p-n接合の単位面積あたりの容量は
Cj=εsi/Wdj=√(εsi・q・Na/(2(ψbi+Vj)))
Wdjは空乏層幅、Naは低濃度側のDoping濃度 Vjは逆方向バイアス電圧
ψbiは内蔵電位≒0.9Vである。
ドレイン電圧が高くなると空乏層幅が広がり容量が減少する。Naが増えると接合容量が増加するので不必要に高い不純物プロファイルを作るべきではない。
拡散層と基板との容量の総和はCjにレイアウト上の拡散層面積をかけたものに等しい。
Cj=WdCj
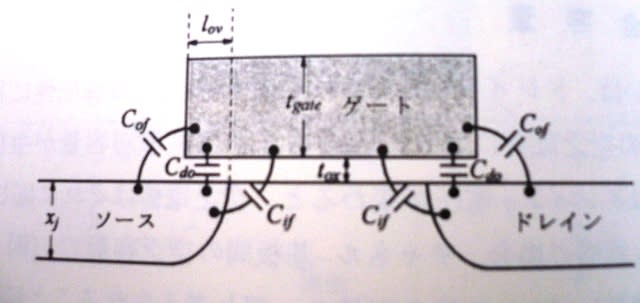
オーバーラップ容量は図のように直接オーバーラップ、内部フリンジ、外部フリンジの3成分からなる。
直接オーバーラップCdo=W・lov・Cox=εox・W・lov/tox
内部フリンジCif=2εox・W/π・ln(1+xj/2tox)
外部フリンジCof=2εox・W/π・ln(1+tgate/tox)
tgateはPoly-Siゲートの高さである。
内部フリンジは反転層が形成されると静電的に遮蔽されるために消滅する。
ゲート外へのホットキャリア注入による信頼性の悪化を避けるために直接OverLap長は最低lov≒2~3tox必要だと言われている。
ソース・ドレイン抵抗
特にソース側の抵抗はゲートのドライブ電圧を減らす役割をするので問題となる。

図はS/D領域における電流の流れを示したものである。S/D抵抗は
Rac G-S、G-Dのオーバーラップ部の蓄積層抵抗
Rsp 表面層からS/Dの深さまで電流が流れる部分の抵抗
Rsh 電流が均一に流れている部分の抵抗
Rco 電流がコンタクト部分に流れ込む領域のコンタクト抵抗
コンタクトのメタル部分は非常に抵抗は低くなるので
Alの場合 0.05Ω/□ ⇔ チャネルシート抵抗 2000~7000Ω/□
Rcoはほとんど無視できる。
蓄積層抵抗Racはゲート電圧に依存し、Racは実効チャネル長Leffの一部だとして考えることが出来る。

Rspは図のような電流の広がりが均一にDopeされた抵抗体の中で生じるとの仮定の下に求められている。
Rsp=2ρ/(π・W)・ln(0.75・xj/xc)
ここでWはデバイス幅、xjは接合深さ、xcは反転層厚さである。
典型的なxj/xc≒40と言う値に対しRsp≒2・ρ/Wが得られる。
しかしながら実際には電流の広がりは横方向の不純物勾配により局所的に抵抗率が均一で無い領域で起こるため詳細な解析はSimulationをする必要がある。一般的にはRac+Rspの和が最小になるように電流が流れる。
急峻なS/D不純物Profileを作った場合はRac、Rspは共に低くLeff=Lmetである。
一方で勾配の緩やかなProfileの場合にはRac、Rspが大きくなりLeff>Lmetである。
S/D拡散層のシート抵抗は
Rsh=ρsd・S/W
ρsdはS/Dの抵抗率、Wはデバイス幅、Sはゲート端とコンタクト端との距離
ρsdは50-500Ω/□の値が一般的である。Sはゲート幅に合わせてなるべく多くのコンタクトを配置することによって小さく出来る。
コンタクト抵抗
Rco=√(ρsd・ρc)/W・coth(lc・√(ρsd/ρc))
ρcはコンタクト部分の抵抗率、lcはコンタクト開口幅である。
Rcoにはコンタクト直下の電流集中による抵抗が含まれる。
拡散層のシリサイド化が行われていない場合、コンタクトの大きさにより長コンタクトと短コンタクトの極限を持つ。
短コンタクトは抵抗がコンタクト幅に依存する場合であり
Rco=ρc/(W・lc)
長コンタクトの場合は電流はコンタクトのゲート側に流れ込むためlcに依存しない
Rco=√(ρsd・ρc)/W
金属⇔高濃度Dopeシリコン間のオーミックコンタクトでは伝道電流がトンネリング、電界放出に支配される。コンタクト抵抗は障壁高さψBと表面濃度Ndに指数関数的に依存する。
ρc ∝ exp(4πψB/qh・√(m*・εsi/Nd))
hはプランク定数、m*は有効質量である

サリサイド技術を用いた場合はS/Dの抵抗よりも大幅にサリサイド部分の抵抗が低くなるのですべての電流が引き込まれスペーサ下部の抵抗のみが貢献する。
また拡散層全体がコンタクト領域になるので拡散層幅d=コンタクト幅lcになり長コンタクトの極限が適用できる。一方でS/Dの拡散層抵抗はシリサイドで高濃度層が消費されるために高くなることに注意する必要がある。
寄生容量

MOSFETには真性の容量成分:Cg、Cdに加えて寄生容量が存在する。
S/D拡散層⇔基板の接合容量、Gate-S/D領域のOverLap容量が挙げられる
S/Dと基板は反対の導電性にドーピングされているので接合拡散層容量が生じる。
p-n接合の単位面積あたりの容量は
Cj=εsi/Wdj=√(εsi・q・Na/(2(ψbi+Vj)))
Wdjは空乏層幅、Naは低濃度側のDoping濃度 Vjは逆方向バイアス電圧
ψbiは内蔵電位≒0.9Vである。
ドレイン電圧が高くなると空乏層幅が広がり容量が減少する。Naが増えると接合容量が増加するので不必要に高い不純物プロファイルを作るべきではない。
拡散層と基板との容量の総和はCjにレイアウト上の拡散層面積をかけたものに等しい。
Cj=WdCj

オーバーラップ容量は図のように直接オーバーラップ、内部フリンジ、外部フリンジの3成分からなる。
直接オーバーラップCdo=W・lov・Cox=εox・W・lov/tox
内部フリンジCif=2εox・W/π・ln(1+xj/2tox)
外部フリンジCof=2εox・W/π・ln(1+tgate/tox)
tgateはPoly-Siゲートの高さである。
内部フリンジは反転層が形成されると静電的に遮蔽されるために消滅する。
ゲート外へのホットキャリア注入による信頼性の悪化を避けるために直接OverLap長は最低lov≒2~3tox必要だと言われている。