1995年に、ジョー・ボルチンスキーは、「ブレーン」を超弦理論に取り込む上で重要なアイデアを考え出し、そこで使う「膜」のことを「D-ブレーン」と呼んだ。
それまでの超弦理論では、素粒子としてのひもは「閉じた輪」のようなものだと考えられていた。
そして、重力を伝える重力子と呼ばれる粒子もまた、閉じた弦がある振動の仕方をしているものだと思われていた。
ボルチンスキーがD-ブレーンのアイデアを提案するまでは、超弦理論の研究はもっぱらこのような「閉じた輪」にかぎられていた。
しかしボルチンスキーは、それに加えて「両端のある開いた弦」があってもいいだろうと考えた。
ブラックホールの近くをたくさんの閉じた弦が飛び回っているとしても、ブラックホールの表面は「事象の地平線」なので、その中の様子は遠方からは観測することはできない。そのため、閉じた弦の半分だけが、たまたま事象の地平線を越えて中に入ったとすると、「両端のある弦」がブラックホールの表面に張りついているように見える。
このような考察から、ボルチンスキーは、ブラックホールの表面には開いた弦の端が張りついているものと考え、ほかの「ブレーン」でも同様に、開いた弦の端はその表面に張りついていると考えた。
ストロミンガーとヴァッファは、その量子ミクロ状態の計算から導かれるエントロピーと、一般相対論に基づくベッケンシュタイン=ホーキングの面積公式から得られる値とを比較するという研究計画を考えた。
問題自体は新しくなかったが、二人は、ひも理論だけでなく、ボルチンスキーによるD-ブレーンの発見と、M理論の登場 - いずれも二人の論文が発表される前年の一九九五年になされた - に基づく新たな道具をそれに用いた。
ボルチンスキーは、「D-ブレーンはブラックホールと同じ種類の電荷、および同じ質量と張力をもっており、両者は同じように見える」と指摘した。
しかし、一方を使ってもう一方の性質、たとえばエントロピーを計算できるなら、その類似性は単なる偶然の一致よりはるかに強力だということになる。
それこそがストロミンガーとヴァッファがとったアプローチで、二人はひも理論とM理論に従い、D-ブレーンを使って新しい種類のブラックホールを構築した。
D-ブレーンとひも(一次元のD-ブレーン)からブラックホールを組み立てられる可能性は、D-ブレーンの「双対的」記述に由来する。
ブレーンやひもに作用する力がすべて弱い(カップリングが弱い)モデルでは、ブレーンは膜状の薄い物体として考えることができ、周囲の時空にほとんど影響を及ぼさず、ブラックホールとは似ても似つかない。
一方、カップリングが強く、相互作用の強度が大きい場合、ブレーンは高密度の重い物体となり、事象の地平面と強い重力的影響をもつようになる。
要するに、ブラックホールと見分けがつかなくなる。
しかし、ブラックホールをつくるには、重いブレーン一枚、あるいは重いブレーンの束だけでは足りない。
それを安定化させる何らかの方法が必要だが、そのもっとも簡単な方法が、ブレーンを、何か縮まない安定なものに巻きつけるというものだ。
問題は、強力な輪ゴムから手を離すと縮まって小さな塊になるように、「張力」(単位長さ、面積、体積あたりの値として測定される)の大きい物体は小さく縮まり、それを食い止める何らかの内部構造がないとほぼ消滅してしまうことだ。
その鍵は、系の基底状態、すなわち真空状態がどんどん低いエネルギーレベルへ落ちていくのを防いでくれる、超対称性だった。
ひも理論における超対称性には、その性質が自動的に組み込まれているカラビ=ヤウ多様体が伴うことが多い。
そこで問題は、カラビ=ヤウの中に存在する部分曲面として、ブレーンを巻きつけられるような安定なものを探すことへ行き着く。
空間全体より次元の低いそれらの部分曲面、あるいは部分多様体を、物理学者はサイクルと呼び、多様体の一部を取り囲む、あるいは貫く、縮まないループとしてイメージする(ループは一次元物体に限られるが、サイクルはより高次元にも存在し、縮まない高次元の「ループ」と考えることができる)。
物理学者の見方によれば、サイクルは、巻きつける物体や穴のトポロジーにのみ依存し、その物体や穴の幾何には左右されない。
本来、数学的には、サイクルは単にトポロジーの性質なので、それ自体はブラックホールと何の関係もなく、形状を変えると、サイクルは変わらないが部分多様体は変化する。
しかし、カラビ=ヤウの中には、ブレーンでくるむことができるサイクルが、円、球面、さまざまな次元のトーラス、あるいは種数の大きいリーマン面というように何種類も存在する。
サイクルの数を数える、つまりD-ブレーンを配置する方法が何通りあるかを数えるというのは、微分幾何学の問題で、その数はある微分方程式の解の個数に対応する。
そこでストロミンガーとヴァッファは、ブラックホールのミクロ状態を数え、そのエントロピーを計算するという問題を、幾何学の問題へ変換した。
それは、カラビ=ヤウ多様体の中にD-ブレーンを入れ、望みの質量と電荷をもつようにさせる方法は何通りありえるか、という問題だ。
これはサイクルを使っても表現できる。
つまり、カラビ=ヤウの中に、球面などブレーンでくるめられる最小サイズの形状を何個詰め込めるか?
これらの問題の答えは、当然、与えられたカラビ=ヤウの幾何に左右される。
幾何を変えれば、考えられる配置の数、あるいは球面の数も変わるはずだ。
一般的な描像は以上のとおりだが、計算はやはりとても難しいので、二人はたっぷり時間をかけて、この間題をうまく解けるようにする方法を探した。
そして最初の逃げ道として、四次元K3曲面と円との積からなる五次元内部空間という、とても特別なケースを選んだ。
さらに、平坦な五次元空間に存在する五次元ブラックホールを構築し、D-ブレーンから組み立てられる構造と比較できるようにした。
それは従来のブラックホールとはまったくの別物であり、都合よく選んだ特別な性質のおかげで問題が処理できるようになっていた。
その性質とは、超対称的で「極値的」 - ある電荷において許される最小の質量をもつ - というものだ(超対称的ブラックホールが意味をもつのは、それが存在する背景の真空も超対称性を保つ場合に限られる。私たちの住む低エネルギーの領域では、粒子の超対称性が見られず、そのようにはならない。天文学者が観測しているブラックホールにも、超対称性は見られない)。
カスタムメイドのブラックホールをつくったストロミンガーとヴァッファは、ベッケンシュタイン=ホーキングの公式を使って、事象の地平面の面積からエントロピーを計算した。
次のステップは、内部空間にD-ブレーンを配置し、全電荷と質量をこの特製ブラックホールと一致させる方法が何通りあるかを数えることだった。
そうして求めたエントロピー(状態の数の対数に等しい)を、地平面の面積の計算から得た値と比較したところ、完壁に一致した。
二〇年間挑戦した末に、ついに、統計力学からはじめてブラックホールのエントロピーを導くことができた。
D-ブレーンとブラックホールの関係がいっそう強固になり、D-ブレーンの記述自体が基本的であることも示された。
ストロミンガーとヴァッファ、そしてひも理論にとって、これは大きな成功だった。
D-ブレーンはさらに分割できるのか、もっと小さい部品からできているのか、と思われるかもしれないが、いまでは、ブレーンにはそれ以上の構造はないことがわかっている。
正しいエントロピーが得られ、エントロピーは定義上、すべての状態の数だからだ。
もしブレーンが複数の部品からできていたら、新たに自由度が増え、エントロピーの計算においてさらなる組み合わせを考慮しなければならなくなる。
しかし、一九九六年の結果は、そうはならないことを示している。
ブレーンが存在のすべてなのだ。
次元の異なるブレーンは互いに違って見えるが、いずれも構成部品をもたず、それ以上分割できない。
同じように、ひも理論では、ひもが存在のすべてであり、より小さな部品に分割することはできない。
最初は、ブラックホールの情報のパラドックスはカラビ=ヤウ多様体と何の関係もなさそうに見えた。
ところが、その問題に答える鍵は、実はカラビ=ヤウの中の数学的物体を数えることだったのである。
最新の画像[もっと見る]
-
 タイムトラベルとタイムマシン?
10年前
タイムトラベルとタイムマシン?
10年前
-
 パウリの夢の数式に「虚数」が生み出された!
10年前
パウリの夢の数式に「虚数」が生み出された!
10年前
-
 「微細構造定数」137とパウリ&ユング
10年前
「微細構造定数」137とパウリ&ユング
10年前
-
 宇宙インフレーション 超弦理論
11年前
宇宙インフレーション 超弦理論
11年前
-
 拡張標準モデルとは?
11年前
拡張標準モデルとは?
11年前
-
 拡張標準モデルとは?
11年前
拡張標準モデルとは?
11年前
-
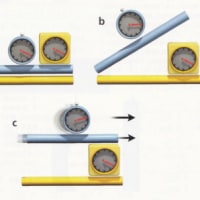 相対性理論とローレンツ対称性
11年前
相対性理論とローレンツ対称性
11年前
-
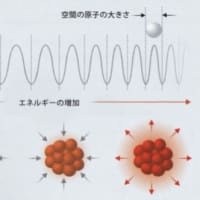
 宇宙の起源に新説か?
11年前
宇宙の起源に新説か?
11年前
-
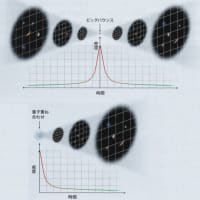
 宇宙の始まりは「ビッグバウンス」?
11年前
宇宙の始まりは「ビッグバウンス」?
11年前
-
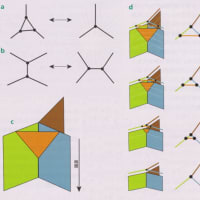 「スピンの泡」が時空に対応する、ループ量子重力
11年前
「スピンの泡」が時空に対応する、ループ量子重力
11年前










※コメント投稿者のブログIDはブログ作成者のみに通知されます