♪潮の満ち引きはなぜ起こる

　潮の満ち引き（潮汐）はなぜ起こる。これは古くて新しいけっこうやっかいな問題なのだ。よく見られる説明としては、地球の月に面した側においては月の引力に引っ張られて海水が上昇して満潮になり、その反対側（裏側）では地球の自転の遠心力などによりこちらも満潮になる・・・といったものだ。この説で問題となるのは地球の裏側だ。地球の自転による遠心力といってるけど、残念ながら地球の自転の遠心力は地球の裏側だけではなく、地軸を中心とした地球の回転面すべてに及んでいるはずである。だからこの説はやっぱりおかしい。ま、これは小学生レベルの子供だましの説明といえるだろう。

　で、ちゃんとした説明としては次のようなものがあるようである。

１．月の真下の（月に面した）海面では月に最も近いため、月からの引力は地球の中心よりも強く働いており、より強く月に引きつけられる。そのため、上向きの力が働いて満潮になる。逆に月の反対側の海面では月から最も遠いため、地球の中心よりも弱い引力しか働いていず、そのため残りの地球のほうがより強く月にひきつけられ、海はあとにとり残されて海水がうしろに置き去りにされるようなかたちで見かけ上上向きに力が働いて満潮となる。

２．月と地球は共通の重心のまわりを周期27日で互いに公転している。地球の月に面している側の海面では、月の引力が最大となるので満潮となる。逆に月の反対側の海面では月の引力は最小となり、月ー地球共通重心に対する公転による遠心力のほうが月の引力よりも優勢になるのでやはり満潮になる。

　１の説も２の説も、月に面した側の海面と月の反対側の海面では上向きの力が働くという点で一致している。それならその両側においては、海面だけでなく地表上のあらゆる事物（人間も含めて）に対しても上向きの力が働くはずなのではないのか。海は液体で、しかもカスピ海なんかよりも圧倒的にでかいから見かけ上の力の作用も派手に現れるとでもいうのか。

　確かに地表も引っ張られはするけれど、さすがに月の引力程度の力では動かされない。しかし動きやすい海水は、その程度の力であっても上へ引っ張られてしまうのだ。カスピ海など、大きな湖沼においても規模は小さいが潮汐はあるという。

　まあ、それはおいておくとして、月の反対側における上向きの力の説明として、１の説では、引力からとり残された海面には見かけ上上向きの力が働くとしているが、これは正しいのかどうかはわからないけれど日常感覚とはどうもフィットしない。

　というわけで、２の説のほうがもっともらしい気がする（JAXA（宇宙航空研究開発機構）の運営する宇宙情報センターというサイトの月の引力が引き起こす潮の満ち引きという記事でもこの説をとっている）。確かにもっともらしいのだが、月ー地球共通重心に対する公転による遠心力なるものをどうとらえるかが問題だ。そう簡単なことではないので、そのへんのところを以下に解説していこう。

　宇宙の星というのはすべて何らかの運動を行っている。すべての星は公転（何かしらの周りを回る）をし、ごく一部の例外をのぞいてはほぼすべての星が自転（自分自身が回転する）をしている。

　月は地球の周りを公転しているといわれる。月の満ち欠けが周期的に見られるというのがその証拠というわけだ。その周期は29.5日で、旧暦（≒太陰暦）ではこれが1ヶ月の長さとなっている。

　しかし、実際の月の公転周期は29.5日ではなく27.3日である。では、月の公転周期とはいったい何なのか？

　順を追って説明していこう。まず月と地球は、両者の中心を結ぶ直線上の一点（共通重心）を中心として互いに回転運動をしている。つまり互いに公転し合っているのだ。この共通重心というのは、地球のほうが圧倒的に重いので地球の内部にもぐったところにある（地球半径の約27％の深さのところ）。下図のB点が共通重心である。月と地球は互いの引力によって引かれ合い、共通重心の周りを互いに公転し合っている。月が誕生する以前の地球は地軸が安定せず、グラグラ揺れていたという。その揺れが止まったのは、月ができて、月と地球とが互いの引力によって引かれ合い公転し合うことで地球の地軸が安定したからだ。

　ところで、下図を見るかぎり共通重心から最も近い地表面の遠心力が最小で、その裏側の地表面（共通重心から最も遠い地表面）では遠心力が最大となるような気がする。しかしことはそう簡単ではないのだ。そこらのことはもう少しあとで明らかにしていこう。

図１　

　さて、公転周期とは何かというと、共通重心の周りを月と地球が公転し合う周期のことだ。それが27.3日なのである。この周期にまったく同期して、月は１自転する。つまり月の自転周期＝月の公転周期である。その結果、月は常に同じ面を地球に向けたまま地球を一周する。

　ではなぜ月の公転周期と月の満ち欠け周期は一致しないのか。月と地球とは、前述したように互いの共通重心を中心として公転し合っている。そしてこの共通重心は、太陽の周りを365日かけて１周する。これがいわゆる地球の公転である。地球が太陽の周りを公転するというより、月と地球の共通重心が公転するというわけだ。さて、月と地球とが公転し合う周期である27.3日の間にも共通重心は太陽の周りを回りつづけている。すると、下図で見られるように満月もその分だけ回った後に訪れることになる。

【地球と宇宙】 月の満ち欠けの周期と月の公転周期がずれる理由 ☜参考までに

　このずれ（2.2日）が27.3日に加算され、29.5日の月の満ち欠けの周期となって現れる。

　では、本題の潮の満ち引きについてはどうであろうか。図1において地球の公転というものをどうイメージすればよいか。地球は自転をしているが、この自転は回転軸（地軸）の回りをクルクルまわる回転で、その回転による遠心力は軸に垂直に外側に向かい全地表面に作用しているので、月に面した側とその裏側とで相殺しあって潮汐には関係ない。

　さて地球の公転はどうか。非常に誤解しやすいのが、共通重心を中心に地球が公転するイメージを、地球を丸いボール紙として、その共通重心に画びょうを差し込んでボール紙をグルグル回転させる様子を思い描いてしまうことである。このイメージでいくと、共通重心から最も近い地表面の遠心力が最小で、その反対（裏）側の地表面（共通重心から最も遠い地表面）では最大となる。だがそう考えてしまうのは、先ほども述べたごとくついおちいりがちな誤解なのだ。

　実は潮汐に関係する地球の遠心力は、現実には下図のようにその大きさも向きも場所を問わずどこも同じなのだ。

　

　以下にそれを説明しよう。実は、共通重心を中心とした地球の公転のイメージというのは下図２（gifアニメ）のようになるのだ（実際には地球は自転もしているがそれは無視している）。太陽だって、地球との共通重心に対して同様な公転をしている（図３）。ただ太陽と地球の場合、あまりに巨大な質量比をもつ星同士なのでその共通重心は太陽のごく中心ちかくにあり、その公転も超ごくわずか（ほぼゼロ）である。ただし、木星は質量が巨大なため太陽との質量比は地球の場合よりも小さく、太陽との共通重心は太陽の外側（太陽表面から約4万8000キロメートル離れたところ）にある。つまり両天体間のごく太陽寄りの空間にある重心を中心にして互いに公転し合っている。

図２ 赤色の十字が共通重心。地球と月のような質量比の大きな天体どうしの場合。月の質量が太陽系全体から見れば超極小なので他の巨大惑星からの影響はほぼ無視できる）

図３ 地球と太陽のごとく質量比が極端に大きな天体どうし（共通重心が太陽中心に近くなっている）

図４ 同じ質量の天体どうし（とびぬけて質量の大きい木星と太陽の場合は、太陽との共通重心は太陽直近になり、その共通重の周りを互いに回転（公転）する。そして、他の巨大惑星（たとえば土星）も太陽との共通重心を中心にして公転することになるので、お互いに影響が出てかなり複雑な運動を行う（Everything in the Solar System orbits the center of mass参照、真ん中の白丸＝太陽、内側の惑星＝木星、外側の惑星＝土星）

以上の図はすべてwikipediaバリセンター（共通重心）より引用

　さて、上図２の地球と月の場合の地球の公転のみをドアップした図が以下だ（回転の向きがマッチしていないがご容赦）。

図５ （wikipediaより引用）

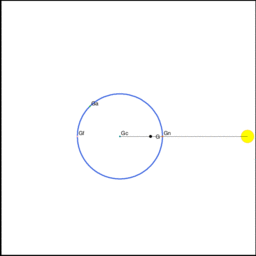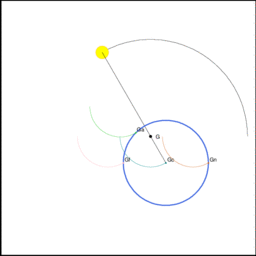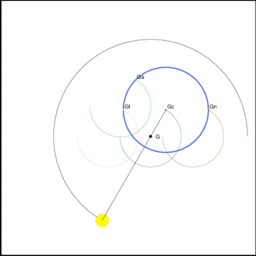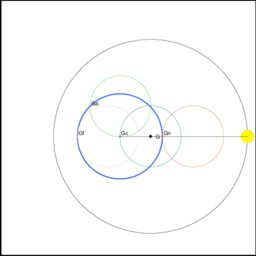
図６ （海の相談室より引用）

　上図上段の図５において、地球中心が共通重心を中心に公転している様子を赤丸で示してある。上図下段の図６を見るとわかるように、地球中心が共通重心を中心に公転すると、地球の他のあらゆる位置も地球中心と同期して地球中心とまったく同じ公転運動を行う。これらの地球中心以外の位置での公転運動群は、共通重心に相当する仮想的な重心を中心として回っている。そして地球のあらゆる位置に存在する物体は、その公転運動に伴ってなされる上下運動はするもののその向きは変わることはない。その様子を示したものが図５である。

　さて、月は地球の引力に引っ張られて落ちつづけながら地球の周りを公転している。そして地球も同様、月の引力に引っ張られながら上図のような公転をしている。このとき、月中心と地球中心には引力とは真反対方向に遠心力を生じている。

　地球の公転運動は、月ー共通重心ー地球中心を結ぶ直線の回転運動（この直線を回転直線１と呼ぶ）ととらえることもできる。この回転直線の一方の端である地球中心には、月の引力とは真反対方向に遠心力が生じている。そして、先に地球中心以外の位置での公転運動群には共通重心に相当する仮想的な重心があると述べたが、それらの各運動群には仮想重心だけではなく仮想的な月ー共通重心ー地球中心（ここから遠心力が生じている）を結ぶ回転直線というものも考えられ、その回転直線群が回転直線１に同期して運動していると考えることもできる。さらに上図６を注視してみると、各回転直線は回転はするものの各直線相互間は平行関係にあることがわかる。で、この回転直線群のある一瞬を切りとった図が以下である。

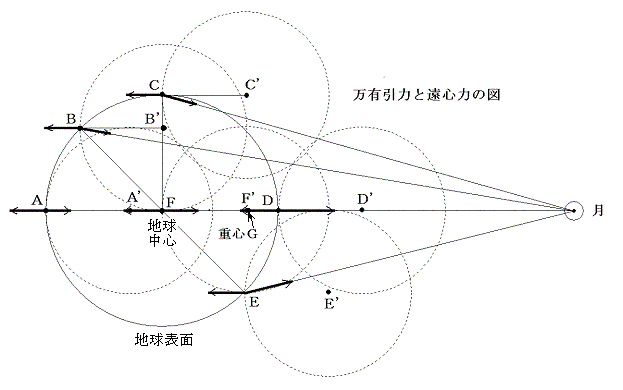
図７ （潮汐力（起潮力） - FNの高校物理より引用）

　上図７において、Fは地球中心、F’（G）は共通重心、FーF’（G）を含む直線が上記でいう回転直線１である。そしてA’～E'は仮想重心、A－A’～E－E’を含む各直線群が、上記でいう地球中心以外の位置において互いに平行関係にある回転直線群だ。A～Fから月中心方向に向けて作用している力は月の引力、A～Fから月とは反対方向（真反対なのはFだけ）へ向けて各々平行に作用している力は遠心力である。これらの遠心力は皆同じ向きだが、大きさも皆等しい。仮想重心A’～E'を中心とした公転運動と共通重心F’（G）を中心とした公転運動とがまったく相似で速度も軌道もまったく同じだからである。これが、先ほど述べた「潮汐に関係する地球の遠心力は、その大きさも向きも場所を問わずどこも同じである」ということの理由である。

　潮の満ち引きを引き起こす力を潮汐力という。この力は上図７において、遠心力と月に向かう月の引力との合力である。下図は地球のさまざまな位置における合力（潮汐力）の様子を示したものである。

　潮汐力が最大になるのはA点とD点で、月から最も遠いA点での潮汐力は「遠心力ー月の引力」である。このA点では月の引力は最小で遠心力より弱くなり、海水は遠心力で上に引っ張られて満潮になる。地球の月に面した側のD点では、月との距離が最短となるため月の引力は最大となる。したがって、この点の遠心力は月の引力に負けて「月の引力ー遠心力」という上向きの力が働き、海水は持ち上げられて満潮となる。他のB、C、E点での合力（潮汐力）はA、D点でのそれよりは小さく、その向きも上向きとはならないので、その力はA、D点での合力よりもずっと弱くなる。

　結局、地球中心ー共通重心ー月を結ぶ線上の月から最も遠い点（A点）と、最も近い点（D点）で満潮が起こるというわけである。地球中心での潮汐力は、遠心力と月の引力とがつり合うためゼロになる。

　そして上記の線と直角をなして地球の中心を貫通する線上にある海では、満ち潮に海水をもっていかれるために水位が下がり、引き潮（干潮）となる。
　いま、月に面した側で満潮となった海は、地球の自転とともに干潮点に達し、地球の裏側で再び満潮となり、さらにもう一つの干潮点に達した後、満潮点に戻って一日が経過する。一日に同じ海で、満潮と引き潮が二度ずつ繰り返されるわけだ。

　ところで、地球のみの公転をドアップした図５と、地球と月どうしの公転の詳細を表した図６を前に示したが、なぜあのような運動になるのかを別の視点から考えてみよう。下図を見てほしい。

　これは地球である。共通重心Gを中心として公転している。地球のあらゆる部位にはこの共通重心Gから遠ざかろうとする遠心力が生じているはずである。その様子をベクトル図で示してある。赤矢印が遠心力である。この遠心力は図からわかるように、月とは反対方向の成分と地球重心とは真反対方向の成分とに分解できる。これらの2力は遠心力の分力なのでやはり遠心力である。つまり、月とは反対方向の成分＝月とは反対方向の遠心力、地球重心とは真反対方向の成分＝地球重心とは真反対方向の遠心力である。そしてこれらの力は地球のあらゆる部位で同時に働く。

　さて、上図の地球円周上のH点におけるベクトル三角形HKIと地球内の三角形GFHとは相似だ。同様に、L点におけるベクトル図三角形LOMと地球内の三角形GFLとは相似だ。そして他の地球円周上のベクトル三角形についても同様のことが言える。よって、地球円周上の各々のベクトルにおける「月とは反対方向の遠心力」は、地球内の三角形の一辺であるGFに比例する。このGFは、どの地球内三角形の場合でも常に同じ位置・同じ長さだ。ということは、各ベクトルの「月とは反対方向の遠心力」は常に同じ大きさ・向きになる。これは地球内部、たとえば上図P点におけるベクトル図においても同じことが言える。

　また、地球円周上の各ベクトルにおける「地球重心とは真反対方向の遠心力」も地球内三角形の半径成分に比例し、よって地球円周上のどのベクトルでの「地球重心とは真反対方向の遠心力」も常に同じ大きさとなる。よって、「地球重心とは真反対方向の遠心力」というのは、地球円周上のあらゆる点において、地球重心とは真反対方向に向け同じ力で同時に作用することになるから互いに打ち消しあい、地球公転には無関係である。

　残るは先述の「月とは反対方向の遠心力」だけで、これだけが地球公転の産物であり、潮汐を引き起こす原因ともなる。

　またどのベクトルでもいいのだが、たとえば地球内部でのベクトル図におけるP点をどんどん地球中心に向けて近づけていくと、PQの長さ（月とは反対方向の遠心力）は変わらないが、Gに対する遠心力（赤矢印）はどんどん小さくなっていってやがてPQと一体となり、そしてそれは地球中心（重心）F点に働く「月とは真反対方向に作用する遠心力」と合致する。

　以上に説明した「月とは反対方向の遠心力＝月とは真反対方向に作用する遠心力」とは、先にいろいろ解説してきた地球公転の産物としての遠心力を力学的な切り口で示したものである。こうした遠心力が働きうる地球の運動というのが先の図５、図６、図７に示した地球の公転図となるわけだ。

　地球が共通重心を中心に公転するというのは、共通重心周りを回っている月の運動に地球が追随して（つられて）回転するといった機構であるが、以下にその機構のイメージ図（gifアニメ）を示す。

潮汐についてより引用

　真ん中にあるのは地球。赤い小さな丸は共通重心。外を回っているのは月。水平に引かれた赤線は便宜的なもので、地球が自転していない（自転は無視している）ことを示す。地球は月の公転に追随して共通重心の周りを公転している。

　赤線上で回転している青い矢印は上述した遠心力である。地球の中心点（重心）に働く遠心力は共通重心の真反対向きに作用している。そしてこの図では省略してあるが地球のその他のあらゆる部分（点）には仮想重心が存在し、その点に対して真反対向きに一様に働く遠心力（地球中心の遠心力と等しい）が働いている。赤線の両端の矢印はそのごく一部の遠心力である。

　ところで、本記事の冒頭で潮の満ち引き（潮汐）はなぜ起こるかという問いに対し２つの答えを示しているが、あれの１のケースは、どうもうまくフィットしないという理由でうやむやにしてしまったが、実は間違いとは言えないのだ。遠心力を使わない潮汐の説明なのである。

　ところで話はこれだけでは終わりません。今まで述べた潮汐力の様子を図にすると以下のようになるのですが

　実は現実的には下図のようになっているともいわれているらしいです。

　　90度（この角度はいろいろなのかもしれません）ひっくりかえっています。

　今まで述べてきた潮汐力の解説は、地球が一様な海水で覆われていて大陸・島嶼 は存在しない、また 海底と海水との摩擦はゼロという仮定（平衡潮汐論（海面がラクビーボールのようになるのはどうして参照））をもとにしたもので、現実の地球の様相とは大きく異なる。上記参照サイトによれば現実には

１．水深の分布は一様ではなく不規則まちまちであり、大陸や島嶼が散在 していて、それらが海水の移動を阻害する。

２．海水にも慣性や摩擦があるため、すぐには潮汐力が追従できないこと。

などがあるため、天文学的理論から導かれた潮汐力のとおりには潮汐は起こらない。

　ところで、太陽も地球に引力を及ぼしているから、太陽による海の満ち引きへの影響も当然ある。しかし、太陽の引力は月の引力にくらべて弱いので、海の満ち引きを起こす力（潮汐力）も弱い。月の潮汐力にくらべ、約半分だ。
　太陽－月－地球の順で一直線に並ぶときの月を新月という。この時期、地球の月に面した側では、月と太陽の引力による満潮が同時に起こるから、潮汐力は最大となる。これを大潮という。また、太陽－地球－月の順で一直線に並ぶときの月が満月だ。この時期、地球の太陽に面した側では、地球の遠心力と太陽の引力による満潮が同時に起こるから、やはり潮汐力は最大となる。これも大潮である。
　世界最大の大河、アマゾン河では、新月と満月の時期になると、河の流れと大潮とが激突し、河水が大音響を発して逆流するそうだ。そういえば、この逆流波に乗ってサーフィンするサーファーたちの映像をテレビで見た覚えがある。

 

☆古代の砂漠に花一輪。女だてらに勇猛果敢、でっかい帝国おっ建てた。その花の名はパルミラ女王ゼノビア。だけど、ここに登場するゼノビアさんは、えっちょっと、とたじろうじゃうかもしんない女王さま・・・なの。⇒パルミラ幻想☆

☆アステカ帝国の興亡と帝国末裔の民が新国家「アストラン」を樹立し、435年後にオリンピックを招致・開催するまでにいたる物語⇒アステカ物語☆

☆宇宙の謎・地球の謎の迷路をへ巡る謎パーク別館⇒＜Sui族館＞☆