算額（その171）

算額（その171）

岐阜県大垣市外野釜笛 釜笛八幡神社 慶応元年(1865)
http://ryugen3.sakura.ne.jp/toukou3/wasankibousya.PDF

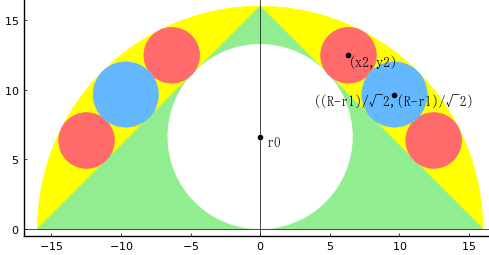
第3問: 半円内に直角二等辺三角形を作り，その隙間に青，赤の 6 個の円を入れる，半円の直径を知って，赤円の径を求めよ。

半円の径を R とする。後々 R は 8 の倍数にしておくほうが方程式の係数が簡単になことがわかる。

白円，青円，赤円の半径を r0, r1,  r2 とし，赤円の中心座標を (x2, y2) とする。

r0, r1 はすぐに計算できる。r2, x2, y2 が未知数であるが，solve() では以下の 4 個の方程式のどの 3 つをとっても，有限の時間内には解が見つからないようである。
そこでいつものように nlsolve で解を求める。

using SymPy

function distance(x1, y1, x2, y2, x0, y0)
   p1, p2 = sympy.Point(x1, y1), sympy.Point(x2, y2)
   l = sympy.Line(p1, p2)
   l.distance(sympy.Point(x0, y0))^2  # 二乗距離を返す！！
end;

@syms R::positive, r0::positive, r1::positive, r2::positive, x1::positive, x2::positive, y2::positive;

R = 16
r0 = R/(1 + sqrt(Sym(2)))
r1 = R*(2 - sqrt(Sym(2)))/4
x1 = (R - r1) / sqrt(Sym(2))
r2 = R // 8
eq1 = distance(R, 0, 0, R, x2, y2) - r2^2
eq2 = x2^2 + y2^2 - (R - r2)^2
eq3 = (x2 - x1)^2 + (y2 - x1)^2 - (r1 + r2)^2
eq4 = x2^2 + (y2 - r0) - (r0 + r2)^2;

println(eq1, ",")
println(eq2, ",")
println(eq3, ",")
println(eq4, ",")

   2*(x2/2 + y2/2 - 8)^2 - 4,
   x2^2 + y2^2 - 196,
   (x2 - sqrt(2)*(4*sqrt(2) + 8)/2)^2 + (y2 - sqrt(2)*(4*sqrt(2) + 8)/2)^2 - (10 - 4*sqrt(2))^2,
   x2^2 + y2 - (2 + 16/(1 + sqrt(2)))^2 - 16/(1 + sqrt(2)),

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]))#, ftol=1e-14)
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini)#, ftol=1e-14)
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (r2, x2, y2) = u
   return [
       2*(x2/2 + y2/2 - 8)^2 - 4,
       x2^2 + y2^2 - 196,
       (x2 - sqrt(2)*(4*sqrt(2) + 8)/2)^2 + (y2 - sqrt(2)*(4*sqrt(2) + 8)/2)^2 - (10 - 4*sqrt(2))^2,
       # x2^2 + y2 - (2 + 16/(1 + sqrt(2)))^2 - 16/(1 + sqrt(2)),
   ]
end;

iniv = [2.0, 6, 12]
res = nls(H, ini=iniv)
println(res)

   ([2.0, 6.352746103452378, 12.475681021293815], true)

経験則で r2 は R の 1/8 となる。
そこで r2 = R // 8 を条件に加えて eq1, eq2 の二元連立方程式を解く。

res = solve([eq2, eq1], (x2, y2))

   2-element Vector{Tuple{Sym, Sym}}:
    (-(sqrt(2) + sqrt(32 - 16*sqrt(2)) + 8)^3/34 - 30*sqrt(32 - 16*sqrt(2))/17 - 30*sqrt(2)/17 - 32/17 + 8*(sqrt(2) + sqrt(32 - 16*sqrt(2)) + 8)^2/17, sqrt(2) + sqrt(32 - 16*sqrt(2)) + 8)
    (-(-sqrt(32 - 16*sqrt(2)) + sqrt(2) + 8)^3/34 - 30*sqrt(2)/17 - 32/17 + 30*sqrt(32 - 16*sqrt(2))/17 + 8*(-sqrt(32 - 16*sqrt(2)) + sqrt(2) + 8)^2/17, -sqrt(32 - 16*sqrt(2)) + sqrt(2) + 8)

x2 が特に複雑な式になり，これが solve() で解が求まらない原因と思われる。

赤円の半径は 半円の径の 1/8 である。

using Plots

function circle(ox, oy, r, color=:red; beginangle=0, endangle=360, fill=false)
   θ = beginangle:0.1:endangle
   x = r.*cosd.(θ)
   y = r.*sind.(θ)
   if fill
       plot!(ox .+ x, oy .+ y, linecolor=color, linewidth=0.5, seriestype=:shape, fillcolor=color)
   else
       plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
   end
end;

function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
   mark && scatter!([x], [y], color=color, markerstrokewidth=0)
   annotate!(x, y, text(string, 10, position, color, vertical))
end;

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   plot()
   R = 16
   r0 = R / (1 + √2)
   r1 = (R - R/√2)/2
   x1 = (R -r1)/√2
   r2 = R // 8
   (x2, y2) = res[1]
   (x22, y22) = res[2] 
   circle(0, 0, R, :yellow, fill=true, beginangle=0, endangle=180)
   plot!([R, 0, -R, R], [0, R, 0, 0], linecolor=:palegreen2, linewidth=0.5, seriestype=:shape, fillcolor=:palegreen2)
   circle(0, r0, r0, :white, fill=true)
   circle(x2, y2, r2, :indianred1, fill=true)
   circle(x22, y22, r2, :indianred1, fill=true)
   circle(x1, x1, r1, :steelblue1, fill=true)
   circle(-x2, y2, r2, :indianred1, fill=true)
   circle(-x22, y22, r2, :indianred1, fill=true)
   circle(-x1, x1, r1, :steelblue1, fill=true)
   if more == true
       point(x2, y2, "(x2,y2)", :black)
       point(x1, x1, "((R-r1)/√2,(R-r1)/√2)", :black, :center)
       point(0, r0, " r0", :black)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
      plot!(showaxis=false)
   end
end;