算額（その940）

算額（その940）

福岡県朝倉市上秋月（旧甘木市秋月町） 秋月八幡宮絵馬堂 明治7年(1874)
「算額」第三集 全国調査，香川県算額研究会

外円に内接する正五角形に一本の対角線を引き，中円と小円を入れる。中円と小円の直径が与えられたとき，対角線の長さを求めよ。

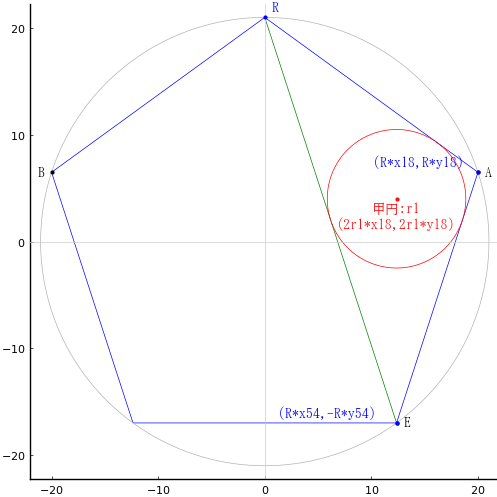
外円の大きさを確定するために必要なのは中円の直径だけであり，小円は無関係である。

算額（その937）の一部分で，求めるものが違うだけである。

座標の定義に使う三角関数の値
(x18, y18) = (cosd(18), sind(18))
(x54, y54) = (cosd(54), sind(54))

正五角形が内接する外円の半径と中心座標を R, (0, 0)
中円の半径と中心座標を r1,(2r1*x18, 2r1*y18)
とおき，以下の方程式より R を得る。

外円の半径は中円の半径の (1 + √5) 倍である。

include("julia-source.txt");

@syms x18::positive, y18::positive, x54::positive, y54::positive
(x18, y18) = (cosd(Sym(18)), sind(Sym(18)))
(x54, y54) = (cosd(Sym(54)), sind(Sym(54)));

@syms R::positive, r1::positive
eq1 = dist2(0, R, R*x54, -R*y54, 2r1*x18, 2r1*y18, r1)
R = solve(eq1, R)[1] |> sympy.sqrtdenest |> simplify
R |> println

   r1*(1 + sqrt(5))

外円の半径が R のとき，求める対角線の長さは RE = AB = 2R*cosd(18)である。

最終的に，

中円の半径が 6.5 のとき，R = 6.5*(1 + sqrt(5))，RE = 2 * 6.5*(1 + sqrt(5)) * cosd(18) = 40.00988598327829 である。

2 * 6.5*(1 + sqrt(5)) * cosd(18)

   40.00988598327829

function draw(more=false)
   pyplot(size=(600, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (x18, y18) = (cosd(18), sind(18))
   (x54, y54) = (cosd(54), sind(54))
   r1 = 6.5
   (x1, y1) = 2r1.*(x18, y18)
   R = r1*(1 + √5)
   l = 2 * r1*(1 + sqrt(5)) * cosd(18)
   println("中円の直径が $(2r1) のとき，対角線の長さは $l")
   x = R .* [x18, 0, -x18, -x54, x54, x18]
   y = R .* [y18, 1, y18, -y54, -y54, y18]
   plot(x, y, color=:blue, lw=0.5)
   circle(0, 0, R, :gray70)
   segment(0, R, R*x54, -R*y54, :green)
   circle(2r1*x18, 2r1*y18, r1)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(R*x18, R*y18, " A", :black, :left, :vcenter)
       point(-R*x18, R*y18, "B ", :black, :right, :vcenter)
       point(R*x54, -R*y54, " E", :black, :left, :vcenter)
       point(0, R, " R", :blue, :left, :bottom, delta=delta/2)
       point(R*x18, R*y18, "(R*x18,R*y18)  ", :blue, :right, :bottom, delta=delta/2)
       point(R*x54, -R*y54, " (R*x54,-R*y54)   ", :blue, :right, :bottom, delta=delta/2)
       point(2r1*x18, 2r1*y18, "甲円:r1\n(2r1*x18,2r1*y18)", :red, :center, delta=-delta/2)
       plot!(xlims=(-1.1R*x18, 1.1R*x18))
   end
end;