算額(その416)
群馬県高崎市榛名山町 榛名神社 明治33年(1900)
早坂平四郎: 算額の一考察,苫小牧工業専門学校紀要
https://www.tomakomai-ct.ac.jp/wp01/wp-content/uploads/2014/06/kiyou5-8.pdf
埼玉県加須市 秋葉山本坊(秋葉宮) 文化5年(1808)2月
http://www.wasan.jp/saitama/akibahonbo1.html
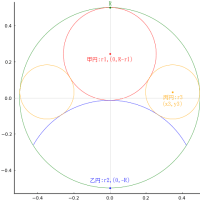
円内に大円1個,中円2個,小円2個が入っているこれらは互いに内接・外接している他2,弦を共通接線としている。中円,小円の半径がわかっているとき,大円の半径を求めよ。

外円の半径と中心座標を r0, (0, 0)
大円の半径と中心座標を r1, (0, y1)
中円の半径と中心座標を r2, (r2, y2)
小円の半径と中心座標を r3, (r3, y3)
弦の端点座標を (xa, ya), (xb, yb) ただし,ya^2 = r0^2 - xa^2, yb^2 = r0^2 - xb^2
solve() では解ききらないので nlsolve() で数値解を求める。
include("julia-source.txt");
using SymPy
@syms r0::positive, r1::positive, y1::positive,
r2::positive, y2::negative, r3::positive, y3::positive,
xa::positive, ya::negative, xb::positive, yb::positive;
(r2, r3) = (15, 5)
eq1 = r3^2 + y3^2 - (r0 - r3)^2
eq2 = r2^2 + y2^2 - (r0 - r2)^2
eq3 = r3^2 + (y3 - y1)^2 - (r1 + r3)^2
eq4 = r2^2 + (y1 - y2)^2 - (r1 + r2)^2
eq5 = distance(xa, ya, xb, yb, 0, y1) - r1^2
eq6 = distance(xa, ya, xb, yb, r2, y2) - r2^2
eq7 = distance(xa, ya, xb, yb, r3, y3) - r3^2;
eq8 = xa^2 + ya^2 - r0^2
eq9 = xb^2 + yb^2 - r0^2;
# res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8, eq9], (r0, r1, y1, y2, y3, xa, xb))
using NLsolve
function nls(func, params...; ini = [0.0])
if typeof(ini) <: Number
r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
v = r.zero[1]
else
r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
v = r.zero
end
return v, r.f_converged
end;
function H(u)
(r0, r1, y1, y2, y3, xa, ya, xb, yb) = u
return [
y3^2 - (r0 - 5)^2 + 25, # eq1
y2^2 - (r0 - 15)^2 + 225, # eq2
-(r1 + 5)^2 + (-y1 + y3)^2 + 25, # eq3
-(r1 + 15)^2 + (y1 - y2)^2 + 225, # eq4
-r1^2 + (y1 - (xa^2*yb - xa*xb*ya - xa*xb*yb + xb^2*ya + y1*ya^2 - 2*y1*ya*yb + y1*yb^2)/(xa^2 - 2*xa*xb + xb^2 + ya^2 - 2*ya*yb + yb^2))^2 + (xa*y1*ya - xa*y1*yb - xa*ya*yb + xa*yb^2 - xb*y1*ya + xb*y1*yb + xb*ya^2 - xb*ya*yb)^2/(xa^2 - 2*xa*xb + xb^2 + ya^2 - 2*ya*yb + yb^2)^2, # eq5
(y2 - (ya*(xa^2 - 2*xa*xb + xb^2 + ya^2 - 2*ya*yb + yb^2) - (ya - yb)*(xa^2 - xa*xb - 15*xa + 15*xb - y2*ya + y2*yb + ya^2 - ya*yb))/(xa^2 - 2*xa*xb + xb^2 + ya^2 - 2*ya*yb + yb^2))^2 + (-(xa*(xa^2 - 2*xa*xb + xb^2 + ya^2 - 2*ya*yb + yb^2) - (xa - xb)*(xa^2 - xa*xb - 15*xa + 15*xb - y2*ya + y2*yb + ya^2 - ya*yb))/(xa^2 - 2*xa*xb + xb^2 + ya^2 - 2*ya*yb + yb^2) + 15)^2 - 225, # eq6
(y3 - (ya*(xa^2 - 2*xa*xb + xb^2 + ya^2 - 2*ya*yb + yb^2) - (ya - yb)*(xa^2 - xa*xb - 5*xa + 5*xb - y3*ya + y3*yb + ya^2 - ya*yb))/(xa^2 - 2*xa*xb + xb^2 + ya^2 - 2*ya*yb + yb^2))^2 + (-(xa*(xa^2 - 2*xa*xb + xb^2 + ya^2 - 2*ya*yb + yb^2) - (xa - xb)*(xa^2 - xa*xb - 5*xa + 5*xb - y3*ya + y3*yb + ya^2 - ya*yb))/(xa^2 - 2*xa*xb + xb^2 + ya^2 - 2*ya*yb + yb^2) + 5)^2 - 25, # eq7
-r0^2 + xa^2 + ya^2, # eq8
-r0^2 + xb^2 + yb^2, # eq9
]
end;
(r2, r3) = (15, 5)
iniv = [big"40.0", 18, 10, -20.4, 34.1, 32, -24.4, 8.2, 39.1]
res = nls(H, ini=iniv);
println(res);
(BigFloat[38.7638837486628373465473353663136173085470569162791234706045756107292743498459, 17.99038105676657970145584756129404275207103940357785471041855234588949762681627, 10.95152380775283700472801642392206965400276275976845771998475084075123109744924, -18.4315536735230681094936333192018549711528600474534715446198618905612484280433, 33.39161340506353031902486710976142560545305462282349919389008399018128308922975, 32.33934584554869449875985865589356317819349516144509459022026784764907086157268, -21.37300618915924098536769340774952612678627228671598130988515134391456899286098, 8.622548477793335355655385214702161614702564480769434367924497563401166456827728, 37.79272867931013343463889124083200695874231476480976753169233139115218150527541], true)
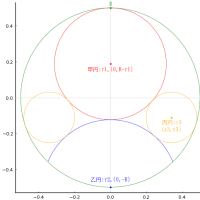
r0 = 38.7639; r1 = 17.9904; y1 = 10.9515; y2 = -18.4316; y3 = 33.3916; xa = 32.3393; ya = -21.373; xb = 8.62255; yb = 37.7927
中円,小円の半径をそれぞれ 15, 5 としたとき,大円の半径は 17.99038105676658 である。
Float64(res[1][2])
17.99038105676658
術によれば,中円,小円の半径を a, b とすると,大円の「直径」は (a + b + 6√(a*b))*(a + b + 2√(a*b))/(4a*b) であるとしている。しかしこれは上述の大円の半径を2倍したものではない。何らかの不適切な式であると思われる。
(a, b) = (15, 5)
(a + b + 6√(a*b))*(a + b + 2√(a*b))/(4a*b)
8.952135486850342
using Plots
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r2, r3) = (15, 5)
(r0, r1, y1, y2, y3, xa, ya, xb, yb) = res[1]
@printf("r0 = %g; r1 = %g; y1 = %g; y2 = %g; y3 = %g; xa = %g; ya = %g; xb = %g; yb = %g\n", r0, r1, y1, y2, y3, xa, ya, xb, yb)
plot()
circle(0, 0, r0, :black)
circle(0, y1, r1)
circle(r2, y2, r2, :orange)
circle(-r2, y2, r2, :orange)
circle(r3, y3, r3, :green)
circle(-r3, y3, r3, :green)
segment(xa, ya, xb, yb, :blue)
segment(-xa, ya, -xb, yb, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) / 3 # size[2] * fontsize * 2
point(r0, 0, " r0", :black, :left, :bottom, delta=delta)
point(0, y1, " y1 大円:r1", :red, :left, :vcenter)
point(r2, y2, " 中円:r2,(r2,y2)", :orange, :center, :top, delta=-delta)
point(r3, y3, " 小円:r3,(r3,y3)", :green, :left, :vcenter)
point(xa, ya, "(xa,ya)", :blue, :left, :top, delta=-delta)
point(xb, yb, "(xb,yb)", :blue, :left, :bottom, delta=delta)
vline!([0], color=:black, lw=0.5)
hline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;