算額（その1001）

算額（その1001）

番外六 広野村川嶋（現嵐山町） 鬼神社 

埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.

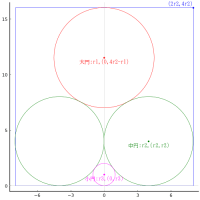
外円（半円）の中に斜線 2 本と，甲円（半円），乙円，丙円を入れる。乙円の直径が与えられたときに，丙円の直径を求めよ。

外円の半径と中心座標を R, (0, 0); R = 2r1
甲円の半径と中心座標を r1, (r1, 0)
乙円の半径と中心座標を r2, (R - r2)
丙円の半径と中心座標を r3, (x3, y3)
とおき，以下の連立法て式を解く。

SymPy の能力的に，一度には解けないので，丙円は後回しにして，「r1 を未知数として」外円，甲円，乙円，および斜線のパラメータを決定する。

include("julia-source.txt");

using SymPy

@syms R::poitive, r1::poitive, r2::poitive, r3::poitive,
     x3::poitive, y3::poitive, x0::poitive, y0::poitive
R = 2r1
#y0 = (x0 + R)/3
eq3 = x0^2 + y0^2 - R^2
eq4 = dist2(-R, 0, x0, y0, 0, R - r2, r2)
eq6 = dist2(-R, 0, x0, y0, r1, 0, r1);
#= 以下の 3 本の式は丙円に関するもの
eq1 = (x3 - r1)^2 + y3^2 - (r1 - r3)^2
eq2 = y3/(x3 - r1) - (x0 + R)/y0
eq5 = dist2(-R, 0, x0, y0, -x3, y3, r3);
=#
# solve([eq1, eq2, eq3, eq4, eq5], (r1, r3, x3, y3, x0))

res1 = solve([eq3, eq4, eq6], (r2, x0, y0))[5]  # 5 of 5

   (-65*r1/8 + 9*sqrt(2)*r1/4 + 3*sqrt(2)*sqrt(r1*(65*r1 + 63*sqrt(r1^2)))*sqrt(9 - 4*sqrt(2))/8 - 63*sqrt(r1^2)/8 + 7*sqrt(2)*sqrt(r1^2)/4, 14*sqrt(r1^2)/9, 8*sqrt(2)*r1/9)

5 組の解が得られるが，5 番目のものが適解である。更に得られる r2 の式は非常に短い形に簡約化できる。
次に，r2, x0, y0 が既知というスタート地点に立って，eq1, eq2, eq5 を解いて丙円の半径 r3 と中心座標 9x3, y3) を決定する。

@syms R::poitive, r1::poitive, r2::poitive, r3::poitive,
     x3::poitive, y3::poitive, x0::poitive, y0::poitive
R = 2r1
r2 = 2r1*(8sqrt(Sym(2)) - 11)  # r2 は超簡約化できる
x0 = 14r1/9
y0 = 8sqrt(Sym(2))*r1/9
eq1 = (x3 - r1)^2 + y3^2 - (r1 - r3)^2
eq2 = y3/(x3 - r1) - (x0 + R)/y0
eq5 = dist2(-R, 0, x0, y0, -x3, y3, r3);
res2 = solve([eq1, eq2, eq5], (r3, x3, y3))[1]  # 1 of 2

   (r1/3, 11*r1/9, 4*sqrt(2)*r1/9)

2 組の解が得られるが，最初のものが適解である。

さて，算額の問は，「乙円の直径がわかっているときに，丙円の直径を求めよということである。
連立方程式を解いて，乙円と丙円の半径 r2, r3 が甲円の半径 r1 でどのように表されるかがわかったので，r2から直接 r3 を求める式 r3/r2 を作ればよい。

@syms r1, r2, r3
r2 = 2r1*(8sqrt(Sym(2)) - 11)
r3 = r1/3
r3/r2 |> simplify |> factor |> println

   (11 + 8*sqrt(2))/42

丙円の直径は，乙円の直径の (11 + 8√2)/42 倍である。

「術」は「置十八箇開平方ニ以減六箇餘以除乙円径得丙円径」と書いてあるが，実際の計算方法は上で述べたものとは異なるようだ。正しいかどうかは筆者にはわからない。

r2 = 3 のときの数値解を求めると r3 = 1.5938363213560542 となり，3 * (11 + 8√2)/42 = 1.593836321356054 と一致する。

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return Float64.(v), r.f_converged
end;

function H(u)
   (r1, r3, x3, y3, x0, y0) = u
   return [
y3^2 + (-r1 + x3)^2 - (r1 - r3)^2,  # eq1
y3/(-r1 + x3) - (2*r1 + x0)/y0,  # eq2
-4*r1^2 + x0^2 + y0^2,  # eq3
16*r1^4 - 16*r1^3*r2 + 16*r1^3*x0 - 16*r1^3*y0 - 16*r1^2*r2*x0 + 8*r1^2*r2*y0 + 4*r1^2*x0^2 - 8*r1^2*x0*y0 + 4*r1^2*y0^2 - 4*r1*r2*x0^2 + 4*r1*r2*x0*y0 - r2^2*y0^2,  # eq4
-4*r1^2*r3^2 + 4*r1^2*y0^2 - 8*r1^2*y0*y3 + 4*r1^2*y3^2 - 4*r1*r3^2*x0 - 4*r1*x0*y0*y3 + 4*r1*x0*y3^2 - 4*r1*x3*y0^2 + 4*r1*x3*y0*y3 - r3^2*x0^2 - r3^2*y0^2 + x0^2*y3^2 + 2*x0*x3*y0*y3 + x3^2*y0^2,  # eq5
r1^2*(-4*r1^2 - 4*r1*x0 - x0^2 + 8*y0^2),  # eq6
   ]
end;
r2 = 3
iniv = BigFloat[25/2, 4, 15, 8, 20, 11]
res = nls(H, ini=iniv)
(r1, r3, x3, y3, x0, y0) = res[1]
res |> println
r3/r2 |> println

   ([4.781508964068163, 1.5938363213560542, 5.844066511638866, 3.005366589152766, 7.43790283299492, 6.010733178305532], true)
   0.5312787737853514

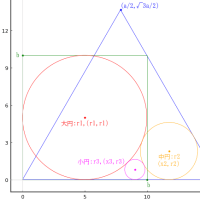
r1 = 1.234 のとき，それぞれのパラメータは以下のとおりである。

r1 = 1.234;  R = 2.468;  r2 = 0.774233;  x0 = 1.91956;  y0 = 1.55124;  r3 = 0.411333;  x3 = 1.50822;  y3 = 0.775618

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 1.234
   R = 2r1
   (r2, x0, y0) = r1 .* (16√2 - 22, 14/9, 8√2/9)
   (r3, x3, y3) = r1 .* (1/3, 11/9, 4√2/9)
   @printf("r1 = %g;  R = %g;  r2 = %g;  x0 = %g;  y0 = %g;  r3 = %g;  x3 = %g;  y3 = %g\n", r1, R, r2, x0, y0, r3, x3, y3)
   plot()
   circle(0, 0, R, :blue, beginangle=0, endangle=180)
   circle(r1, 0, r1, :green, beginangle=0, endangle=180)
   circle(-r1, 0, r1, :green, beginangle=0, endangle=180)
   circle2(x3, y3, r3, :magenta)
   circle(0, R - r2, r2, :orange)
   segment(-R, 0, x0, y0, :gray)
   segment(R, 0, -x0, y0, :gray)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, R, " R", :blue, :left, :bottom, delta=delta/2)
       point(R, 0, " R", :blue, :left, :bottom, delta=delta/2)
       point(r1, 0, "甲円:r1,(r1,0)", :green, :center, :bottom, delta=delta)
       point(0, R - r2, "乙円:r2,(0,R-r2)", :orange, :center, delta=-delta/2)
       point(x3, y3, "丙円:r3\n(x3,y3)", :magenta, :center, :bottom, delta=delta/2)
       point(x0, y0, " (x0,y0)", :gray, :left, :vcenter)
   end
end;