算額（その720）

算額（その720）

長野県諏訪市中洲 諏訪大明神社 天保12年(1841)
中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html

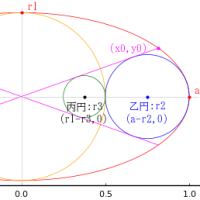
正五角形に 2 本の対角線を引き，区画された領域に大円，中円，小円，正方形を入れる。対角線の長さの 8 乗が 256 となるときの，それぞれの大きさはいかほどか。

図形は相似なので，R = 1 として問題を解き，必要な場合に「対角線の長さの 8 乗が 256 となるとき」という条件下の値を提示する。

まず，基本的な座標を定義する。

正五角形が内接する円の直径を R として 5 個の頂点の座標を以下のように定義する。

include("julia-source.txt");

using SymPy
@syms R::positive, r1, ox1, r2, ox2, r3, ox3, xa, a
R = 1
(x1, y1) = R.*(cos(2PI/20), sin(2PI/20))
(x2, y2) = (0, R)
(x3, y3) = (-x1, y1)
(x4, y4) = R.*(-sin(2PI/10), -cos(2PI/10))
(x5, y5) = (-x4, y4);

それぞれの図形のパラメータは独立して求めることができるので，まず大円の直径 r1 と中心座標 (ox1, y1 - r1) を求める。

eq1 = (y1 - y4)/2 - r1
solve(eq1, r1)[1] |> println
eq2 = (x3 + x5)/2 - ox1;
res1 = solve(eq2, ox1)[1] |> println

   sqrt(5)/4
   sqrt(2)*(-sqrt(sqrt(5) + 5) + sqrt(5 - sqrt(5)))/8

次に，中円の直径 r2 と中心座標 (ox2, y1 + r2) を求める。

@syms d
eq3 = dist(x2, y2, x3, y3, ox2, y1 + r2) - r2^2
eq3 = eq3 = apart(eq3, d) |> simplify
eq4 = dist(x2, y2, x5, y5, ox2, y1 + r2) - r2^2
eq4 = apart(eq4, d) |> simplify
res2 = solve([eq3, eq4], (r2, ox2));
res2[3][1].evalf(), res2[3][2].evalf()

   (0.263932022500210, -0.138757275712888)

次に，小円の直径 r3 と中心座標 (ox3, y1 + r3) を求める。

eq5 = dist(x2, y2, x5, y5, ox3, y1 + r3) - r3^2
eq5 = apart(eq5, d) |> simplify
eq6 = dist(x2, y2, x1, y1, ox3, y1 + r3) - r3^2
eq6 = apart(eq6, d) |> simplify;
res3 = solve([eq5, eq6], (r3, ox3));
res3[1][1].evalf(), res3[1][2].evalf()

   (0.190983005625053, 0.363271264002680)

正方形の一辺の長さを a，右上の頂点の座標を (xa, y1) とおき，以下の連立方程式から a, xa を求める。

eq7 = (x1 - xa)/a - (x1 - x5)/(y1 - y5)
eq8 = (x5 - xa + a)/(y1 - a - y5) - x5/(y2 - y5)
res4 = solve([eq7, eq8], (xa, a))
res4[a].evalf(), res4[xa].evalf()

   (0.440371669705066, 0.807971087145006)

以上により計算された数値は R = 1 のときのものである。
「問」の条件は「対角線の長さの 8 乗が 256 となるとき」，つまり「対角線の長さが 2 のとき」というものである。
R = 1 のとき，対角線の長さは，2x1 = 1.902113032590307 なので 問の条件に従うためには R = 1 で計算された数値を 2/1.902113032590307 = 1.0514622242382672 倍すればよいということになる。

大円の直径 = 1.1755705045849463
中円の直径 = 0.5550291028515503
小円の直径 = 0.40162283177245545
正方形の一辺の長さ = 0.4630341753196083

なお，「答」で提示された数値には誤差があり，また，この数値を 10 倍したものが提示されている。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   R = 1
   (x1, y1) = R.*(cos(2pi/20), sin(2pi/20))
   (x2, y2) = (0, R)
   (x3, y3) = (-x1, y1)
   (x4, y4) = R.*(-sin(2pi/10), -cos(2pi/10))
   (x5, y5) = (-x4, y4)
   plot([x1, x2, x3, x4, x5, x1], [y1, y2, y3, y4, y5, y1], color=:blue, lw=0.5)
   segment(x2, y2, x5, y5, :green)
   segment(x1, y1, x3, y3, :green)
   circle(0, 0, R, :orange)
   r1 = sqrt(5)*R/4
   ox1 = sqrt(2)*R*(-sqrt(sqrt(5) + 5) + sqrt(5 - sqrt(5)))/8
   circle(ox1, y1 - r1, r1, :magenta)
   (r2, ox2) = (0.263932022500210, -0.138757275712888)
   circle(ox2, y1 + r2, r2, :brown)
   (r3, ox3) = (0.190983005625053, 0.363271264002680)
   circle(ox3, y1 + r3, r3, :red)
   (a, xa) = (0.440371669705066, 0.807971087145006)
   rect(xa - a, y1-a, xa, y1, :purple)
   factor = 2/1.902113032590307
   println("大円の直径 = $(r1*2factor)")
   println("中円の直径 = $(r2*2factor)")
   println("小円の直径 = $(r3*2factor)")
   println("正方形の一辺の長さ = $(a*factor)")
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, R, " R", :red, :left, :bottom, delta=delta/2)
       point(xa, y1, "(xa,y1)", :purple, :right, :bottom, delta=delta/2)
       point(xa - a, y1-a, " (xa-a,y1-a)", :purple, :left, :bottom, delta=delta/2)
       point(ox1, y1 - r1, "大円:r1,(ox1,y1-r1)", :magenta, :center, delta=-delta/2)
       point(ox2, y1 + r2, "中円:r2\n(ox2,y1+r2)", :brown, :center, delta=-delta/2)
       point(ox3, y1 + r3, "小円:r3\n(ox3,y1+r3)", :red, :center, delta=-delta/2)
   end
end;