算額（その283）

算額（その283）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額(246)
長野県諏訪市中洲 諏訪大社上社 明治12年(1897)

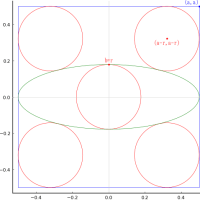
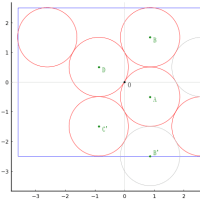
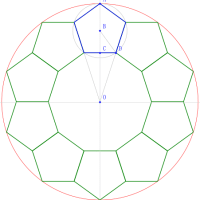
大円内に，正三角形，元円，亨円，利円をそれぞれ 3 個，貞円を 6 個が入っている。それぞれは，大円，正三角形，隣り合う円に接している。

大円の半径，中心座標 R, (0, 0)
元円の半径，中心座標 r1, (x1, r1)
亨円の半径，中心座標 r2, (x2, r2)
利円の半径，中心座標 r3, (0, R - r3)
貞円の半径，中心座標 r4, (x4, R - 2r3 + r4
ここで，
r2 = 16 // 2
r3 = (1//2 - √3/4)R
x1 = (R - r1)√3/2
x2 = (R - 2r1 - r2)√3/2
である。

図のように記号を定め，連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms R::positive, x1::positive, r1::positive, x2::positive, r2::positive,
   r3::positive, x4::positive, r4::positive;

r2 = 16 // 2
r3 = (1//2 - sqrt(Sym(3))/4)R
x1 = (R - r1)sqrt(Sym(3))/2
x2 = (R - 2r1 - r2)sqrt(Sym(3))/2
eq0 = 2r2 + r2 + 2r1 - R
eq1 = (x1 - x2)^2 - 4r1*r2
eq2 = x4^2 - 4r3*r4
eq3 = x1^2 + r1^2 - (R - r1)^2
eq4 = x4^2 + (R - 2r3 + r4)^2 - (R - r4)^2;

変数は R, r1, r4, x4 の 4 個であるが，条件式は5個以上考えられる。この内，適切なものを選択しないと solve() で解が得られないことがある。eq0, eq1, eq2, eq4 の 4 連立方程式を解くことで 2 通りの解が得られるが，最初の解が適切である。また，得られた式が複雑なものもあるが，simplify(), apart() などで単純な数式になる。また evalf() で数値として求めてもよい。

res = solve([eq0, eq1, eq2, eq4], (R, r1, r4, x4))

   2-element Vector{NTuple{4, Sym}}:
    (-64*sqrt(3)*sqrt(4*sqrt(3) + 7)/3 + 152/3 + 128*sqrt(4*sqrt(3) + 7)/3, -32*sqrt(3)*sqrt(4*sqrt(3) + 7)/3 + 40/3 + 64*sqrt(4*sqrt(3) + 7)/3, (41361027804795656 + 23879800537058368*sqrt(3) + 26321303246238494*sqrt(4*sqrt(3) + 7) + 15196611514637565*sqrt(3)*sqrt(4*sqrt(3) + 7))/(6*(1385331749802026 + 799821658665135*sqrt(3))*sqrt(4*sqrt(3) + 7)), sqrt(-1700*sqrt(3)/9 + 1216/(9*sqrt(4*sqrt(3) + 7)) + 3400/9))
    (-128*sqrt(4*sqrt(3) + 7)/3 + 152/3 + 64*sqrt(3)*sqrt(4*sqrt(3) + 7)/3, -64*sqrt(4*sqrt(3) + 7)/3 + 40/3 + 32*sqrt(3)*sqrt(4*sqrt(3) + 7)/3, (-41361027804795656 - 23879800537058368*sqrt(3) + 26321303246238494*sqrt(4*sqrt(3) + 7) + 15196611514637565*sqrt(3)*sqrt(4*sqrt(3) + 7))/(6*(1385331749802026 + 799821658665135*sqrt(3))*sqrt(4*sqrt(3) + 7)), sqrt(-1700*sqrt(3)/9 - 1216/(9*sqrt(4*sqrt(3) + 7)) + 3400/9))

貞円の半径は 4.5 である。元の単位で，丁円の直径は 9 寸である。

names = ("R", "r1", "r4", "x4")
i = 1
for (j, name) in enumerate(names)
   println("$name = $(res[i][j].evalf())")
end

   R = 72.0000000000000
   r1 = 24.0000000000000
   r4 = 4.50000000000000
   x4 = 9.31748562369075

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (R, r1, r4, x4) = res[1]
   r2 = 16 // 2
   r3 = (1//2 - sqrt(Sym(3))/4)R
   x1 = (R - r1)sqrt(Sym(3))/2
   x2 = (R - 2r1 - r2)sqrt(Sym(3))/2
   θ = 0:60:360
   x = [R*cosd(deg) for deg in θ]
   y = [R*sind(deg) for deg in θ]
   @printf("R = %.6f;  r1 = %.6f;  r4 = %.6f;  v4 = %.6f\n", R, r1, r4, x4)
   @printf("2r4 = %.6f\n", 2r4)
   plot([x[1], x[4], x[5], x[2], x[3], x[6], x[1]], [y[1], y[4], y[5], y[2], y[3], y[6], y[1]],
       color=:black, lw=0.5)
   circle(0, 0, R, :black)
   rotate(x1, r1, r1)
   rotate(x2, r2, r2, :blue)
   rotate(0, R - r3, r3, :green)
   rotate(x4, R - 2r3 + r4, r4, :magenta)
   rotate(-x4, R - 2r3 + r4, r4, :magenta)
   if more
       point(0, R, " R", :black, :left, :bottom)
       point(R, 0, "R ", :black, :right, :bottom)
       point(x1, r1, " 元:r1\n (x1,r1)", :red, :left, :top)
       point(x2, r2, " 亨:r2\n (x2,r2)", :blue, :left, :bottom)
       point(0, R - r3, "利:r3 \nR-r3 ", :green, :right, :top)
       point(x4, R - 2r3 + r4, " 貞:r4\n (x4,R-2r3+r4)", :green, :left, :top)
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;