算額(その244)
中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額3(228)
長野県諏訪市下諏訪 諏訪大社下社 慶応4年(1868)
外円の中に大円,小円が 4 個ずつと正方形が入っている。大円の径を知って小円の径を求めよ。
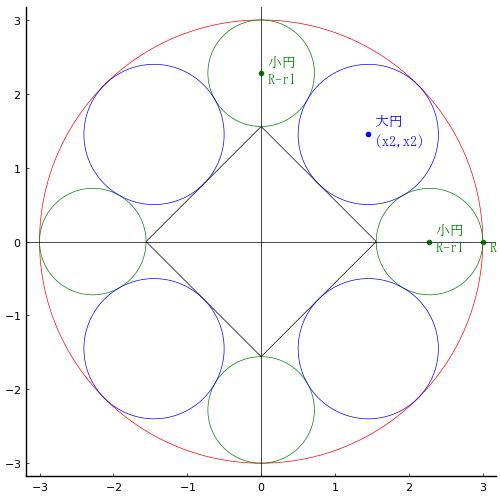
外円の半径,中心座標を R, (0, 0)
大円の半径,中心座標を r2, (x2, x2)
右側の小円の半径,中心座標を r1, (r1, 0)
以下の連立方程式を解く。R は任意なので,R を含む式で求まる。
include("julia-source.txt");
using SymPy
@syms R::positive, r1::positive, r2::positive, x2::positive;
eq1 = (R - r1 - x2)^2 + x2^2 - (r1 + r2)^2
eq2 = 2x2^2 - (R - r2)^2
eq3 = 4(R - 2r2)^2 - 2(R - 2r1)^2 |> expand;
res = solve([eq1, eq2, eq3], (r1, r2, x2))
2-element Vector{Tuple{Sym, Sym, Sym}}:
(R*(-13 - sqrt(467 - 326*sqrt(2)) + 11*sqrt(2))/4, R*(-18 + sqrt(934 - 652*sqrt(2)) + 15*sqrt(2))/8, R*(-15/8 - sqrt(467/64 - 163*sqrt(2)/32) + 13*sqrt(2)/8))
(R*(-3*sqrt(2) + sqrt(19 - 10*sqrt(2)) + 3)/4, R*(-2 + sqrt(2) + sqrt(38 - 20*sqrt(2)))/8, R*(-sqrt(19 - 10*sqrt(2))/8 - 1/8 + 5*sqrt(2)/8))
二番目の解が適切である。
(R*(-13 - sqrt(467 - 326*sqrt(2)) + 11*sqrt(2))/4,
R*(-18 + sqrt(934 - 652*sqrt(2)) + 15*sqrt(2))/8,
R*(-15/8 - sqrt(467/64 - 163*sqrt(2)/32) + 13*sqrt(2)/8)) |> println
(R*(-3*sqrt(2) + sqrt(19 - 10*sqrt(2)) + 3)/4,
R*(-2 + sqrt(2) + sqrt(38 - 20*sqrt(2)))/8,
R*(-sqrt(19 - 10*sqrt(2))/8 - 1/8 + 5*sqrt(2)/8)) |> println
(0.0284330026344626*R, 0.833448221620951*R, 0.117769891910505*R)
(0.240353914715992*R, 0.316402492387137*R, 0.483376433235278*R)
大円の径を知って小円の径を求めるには,比「小円の径 / 大円の径」が分かればよい。
f = res[2][1] / res[2][2] |> expand |> simplify
f |> println
2*(-3*sqrt(2) + sqrt(19 - 10*sqrt(2)) + 3)/(-2 + sqrt(2) + sqrt(2)*sqrt(19 - 10*sqrt(2)))
f |> N
0.7596460852840080105563473006875416586766810646113255778335329777680921720071803
式が複雑なので,f の分母を有理化する。
@syms dummy
f2 = apart(f, dummy)
f2 |> println
-sqrt(19 - 10*sqrt(2))/4 + 1/4 + 3*sqrt(2)/4
有理化後の式 f2 が元の式 f と等しいことを確認する。
f - f2 |> expand |> simplify
0
大円の径が分かれば,0.759646 倍すれば,小円の径になる。
0.949207 * 0.759646 ≒ 0.721062

using Plots
using Printf
function draw(R, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r1, r2, x2) = (R*(-3*sqrt(2) + sqrt(19 - 10*sqrt(2)) + 3)/4, R*(-2 + sqrt(2) + sqrt(38 - 20*sqrt(2)))/8, R*(-sqrt(19 - 10*sqrt(2))/8 - 1/8 + 5*sqrt(2)/8))
@printf("r1 = %.6f; r2 = %.6f; x2 = %.6f; r1/r2 = %.6f\n", r1, r2, x2, r1/r2)
#@printf("x1 = %.5f; y1 = %.5f\n", x1, y1)
plot([R - 2r1, 0, 2r1 - R, 0, R - 2r1], [0, R - 2r1, 0, 2r1 - R, 0], color=:black, lw=0.5)
circle(0, 0, R)
circle(R - r1, 0, r1, :green)
circle(r1 - R, 0, r1, :green)
circle(0, R - r1, r1, :green)
circle(0, r1 - R, r1, :green)
circle4(x2, x2, r2, :blue)
if more == true
point(0, R - 0.9r1, " 小円", :green, :left, :bottom, mark=false)
point(0, R - r1, " R-r1")
point(R - r1, 0.1r1, " 小円", :green, :left, :bottom, mark=false)
point(R - r1, 0, " R-r1")
point(x2, x2 + 0.1r2, " 大円", :blue, :left, :bottom, mark=false)
point(x2, x2, " (x2,x2)", :blue)
point(R, 0, " R")
hline!([0], color=:black, lw=0.5)
vline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;




























※コメント投稿者のブログIDはブログ作成者のみに通知されます