算額（その828）

算額（その828）

宮城県栗原市瀬峰泉谷 瀬峰泉谷熊野神社奉納算額
徳竹亜紀子，谷垣美保，萬伸介：瀬峰泉谷熊野神社奉納算額をめぐる諸問題，仙台高等専門学校名取キャンパス 研究紀要 第60号(2024)
https://www.sendai-nct.ac.jp/natori-library/wp/wp-content/uploads/2024/03/kiyo2024-1.pdf

全円の中に弧を 2 個，甲円 1 個，乙円 3 個を入れる。乙円の直径が 1 寸のとき，甲円の直径はいかほどか。

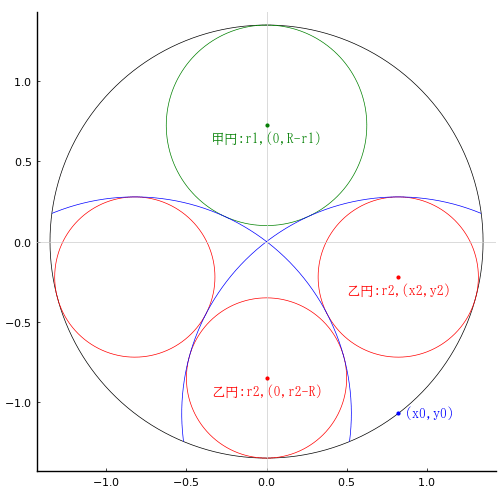
全円の半径と中心座標を R, (0, 0)
甲円の半径と中心座標を r1, (0, R - r1)
乙円の半径と中心座標を r2, (r2 - R), (x2, y2)
全円の円周上にある弧の中心座標を (x0, y0)
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms R::positive, r1::positive, r2::positive, x2::positive, y2::negative, x0::positive, y0::negative
eq1 = x0^2 + (r2 - R - y0)^2 - (R - r2)^2
eq2 = (x0 - x2)^2 + (y2 - y0)^2 - (R - r2)^2
eq3 = x0^2 +(R - r1 - y0)^2 - (r1 + R)^2
eq4 = (x2 + x0)^2 + (y2 - y0)^2 - (R + r2)^2
eq5 = x2^2 + y2^2 - (R - r2)^2
eq6 = x0^2 + y0^2 - R^2;

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return Float64.(v), r.f_converged
end;

function H(u)
   (R, r1, x2, y2, x0, y0) = u
   return [
x0^2 - (R - r2)^2 + (-R + r2 - y0)^2,  # eq1
-(R - r2)^2 + (x0 - x2)^2 + (-y0 + y2)^2,  # eq2
x0^2 - (R + r1)^2 + (R - r1 - y0)^2,  # eq3
-(R + r2)^2 + (x0 + x2)^2 + (-y0 + y2)^2,  # eq4
x2^2 + y2^2 - (R - r2)^2,  # eq5
-R^2 + x0^2 + y0^2,  # eq6
   ]
end;
r2 = 1/2
iniv = BigFloat[2, 1.248, 2.5, -0.7, 0.8, -1.8]
res = nls(H, ini=iniv)

   ([1.3512071919596575, 0.6257139728088581, 0.821951090990108, -0.22124666701222107, 0.821951090990108, -1.0724538589718786], true)

乙円の半径が 1/2 のとき，甲円の半径は 0.6257139728088581 である。
乙円の直径が 1 のとき，甲円の直径は 1.2514279456177162 である。

「術曰」の出だし，「置二分五厘，開立方，名天」は「0.25 の 3 乗根を天と名付ける」でよいだろう。

天 = cbrt(0.25)

   0.6299605249474366

続いて，「四之，」は「これを 4 倍する」
「加一個」は「1を加える」

4天 + 1

   3.5198420997897464

「乗天与一個差」は「1 と天の差を掛ける」（演算数，被演算数が逆になるので注意）

(4天 + 1)*(1 - 天)

   1.3024805228741103

「以除天与一ケ和」は「天と1の和を割る（演算数，被演算数が逆になるので注意）

(天 + 1)/((4天 + 1)*(1 - 天))

   1.2514279456177162

最後に，一般化のために「乗乙円径」で「乙円径を掛ける」

乙円径 = 1
(天 + 1)/((4天 + 1)*(1 - 天))*乙円径

   1.2514279456177162

「答曰」で，「甲円径一寸二分五厘有奇」とあるので，数値解とも一致する。

円弧の描き始めと描き終わりの角度の計算。

@syms R::positive, r1::positive, r2::positive, x2::positive, y2::negative, x0::positive, y0::negative
@syms xa::positive, ya::positive, xb::negative, yb::negative
(R, r1, x2, y2, x0, y0) = [1.3512071919596575, 0.6257139728088581, 0.821951090990108, -0.22124666701222107, 0.821951090990108, -1.0724538589718786]
eq1 = xa^2 + ya^2 - R^2
eq2 = (xa - x0)^2 + (ya - y0)^2 - R^2
res1 = solve([eq1, eq2], (xa, ya))
θ1 = atand(res1[1][2] - y0, res1[1][1] - x0).evalf()
eq1 = xb^2 + yb^2 - R^2
eq2 = (xb - x0)^2 + (yb - y0)^2 - R^2
res2 = solve([eq1, eq2], (xb, yb))
θ2 = atand(res2[1][2] - y0, res2[1][1] - x0).evalf()
(θ1, θ2) |> println

   (67.4673112109364, -172.532688789064)

function draw(more)
    pyplot(size=(500, 500), grid=false, showaxis=true, aspectratio=1, label="", fontfamily="IPAMincho")
   r2 = 1/2
   (R, r1, x2, y2, x0, y0) = res[1]
   @printf("甲円の直径 = %g\n", 2r1)
   (θ1, θ2) = (67.4673112109364, -172.532688789064)
   plot()
   circle(0, 0, R, :black)
   circle(0, R - r1, r1, :green)
   circle2(x2, y2, r2)
   circle(0, r2 - R, r2)
   circle(x0, y0, R, :blue, beginangle=θ1, endangle=360 + θ2, n=500)
   circle(-x0, y0, R, :blue, beginangle=-180 - θ2, endangle=180 - θ1, n=500)
   if more == true
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, R - r1, "甲円:r1,(0,R-r1)", :green, :center, delta=-delta)
       point(0, r2 - R, "乙円:r2,(0,r2-R)", :red, :center, delta=-delta)
       point(x2, y2, "乙円:r2,(x2,y2)", :red, :center, delta=-delta)
       point(x0, y0, " (x0,y0)", :blue, :left, :vcenter)
   end
end;